Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T03:19:20.327Z Has data issue: false hasContentIssue false
  • English
  • Français

A separable quasidiagonal C*-algebra with a non-quasidiagonal quotient by the compact operators

Published online by Cambridge University Press:  24 October 2008

Simon Wassermann
Simon Wassermann
Affiliation:
Department of Mathematics, University of Glasgow, Glasgow G12 8QW, Scotland
Get access Rights & Permissions [Opens in a new window]

Extract

A C*-algebra A of operators on a separable Hilbert space H is said to be quasidiagonal if there is an increasing sequence E1, E2, … of finite-rank projections on H tending strongly to the identity and such that

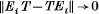
as i → ∞ for T∈A. More generally a C*-algebra is quasidiagonal if there is a faithful *-representation π of A on a separable Hilbert space H such that π(A) is a quasidiagonal algebra of operators. When this is the case, there is a decomposition H = H1 ⊕ H2 ⊕ … where dim Hi < ∞ (i = 1, 2,…) such that each T∈π(A) can be written T = D + K where D= D1 ⊕ D2 ⊕ …, with Di∈L(Hi) (i = 1, 2,…), and K is a compact linear operator on H. As is well known (and readily seen), this is an alternative characterization of quasidiagonality.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 110 , Issue 1 , July 1991 , pp. 143 - 145
Copyright
Copyright © Cambridge Philosophical Society 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Anderson, J.. A C*-algebra A for which Ext(A) is not a group. Ann. of Math. 107 (1978), 455–458.CrossRefGoogle Scholar
[2]Choi, M.-D. and Effros, E. G.. Injectivity and operator spaces. J. Fund. Anal. 24 (1977), 156–209.CrossRefGoogle Scholar
[3]Powers, R. T.. Simplicity of the C*-algebra associated with the free group on two generators. Duke Math. J. 42 (1975), 151–156.CrossRefGoogle Scholar
[4]Wassermann, S.. On tensor products of certain group C*-algebras. J. Fund. Anal. 23 (1976), 239–254.CrossRefGoogle Scholar
[5]Wassermann, S.. C*-algebras associated with groups with Kazhdan's property T (preprint).Google Scholar