Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T16:12:13.171Z Has data issue: false hasContentIssue false
  • English
  • Français

Rotational Specific Heat and Rotational Entropy of Simple Gases at Moderate Temperatures

Published online by Cambridge University Press:  24 October 2008

G. B. B. M. Sutherland
G. B. B. M. Sutherland
Affiliation:
Trinity College
Get access Rights & Permissions [Opens in a new window]

Extract

It is well known that the rotational specific heat of a diatomic gas is given by

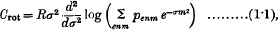
where R is the gas constant, σ = h2/8π2AKT, h is Planck's constant, T is the absolute temperature, K is Boltzmann's constant, and A is the moment of inertia of the molecule.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 26 , Issue 3 , July 1930 , pp. 402 - 418
Copyright
Copyright © Cambridge Philosophical Society 1930

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Fowler, R. H., Statistical Mechanics, p. 34.Google Scholar

† Bulletin of the National Research Council, 1926.

* The usual notation is , but I have used a and b here to avoid confusion with . The formula was thought at one time to have a theoretical basis but is now known to be really empirical.

* Mulliken, , Physical Review, Vol. 28, p. 1221 (1926).Google Scholar

† Ibid. Vol. 30, p. 789 (1927).

* Proc. Camb. Phil. Soc. Vol. 24, p. 280 (1928).CrossRefGoogle Scholar

† Fowler, , Statistical Mechanics, p. 53.Google Scholar

‡ Whittaker, and Watson, , Modern Analysis, 3rd ed. p. 119.Google Scholar

* Whittaker, and Watson, , Modern Analysis, 3rd ed. p. 126.Google Scholar

* Mulliken, , Reviews of Modern Physics, Vol. 1, p. 105 (1930).Google Scholar

† Journal of American Chemical Society, Vol. 51, pp. 2300, 3194 (1929).CrossRefGoogle Scholar

* Van Vleck, , Physical Review, Vol. 28, p. 1016 (1926).CrossRefGoogle Scholar

† Journal American Chem. Soc. Vol. 51, p. 2317 (1929).Google Scholar

* Journal American Chem. Soc. Vol. 48, p. 1520 (1926).CrossRefGoogle Scholar

† Ibid. Vol. 45, p. 2277 (1923).

‡ Ibid. Vol. 51, pp. 2300, 3194 (1929).

* Mulholland, loc. cit.