Hostname: page-component-745bb68f8f-g4j75 Total loading time: 0 Render date: 2025-01-14T02:35:56.707Z Has data issue: false hasContentIssue false
  • English
  • Français

Rolling sphere problems on spaces of constant curvature

Published online by Cambridge University Press:  01 May 2008

V. JURDJEVIC  and
J. ZIMMERMAN
V. JURDJEVIC
Affiliation:
Department of Mathematics, University of Toronto Toronto, Ontario, CanadaM5S 2E4. e-mail: [email protected], [email protected]
J. ZIMMERMAN
Affiliation:
Department of Mathematics, University of Toronto Toronto, Ontario, CanadaM5S 2E4. e-mail: [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The rolling sphere problem on Euclidean space consists of determining the path of minimal length traced by the point of contact of the oriented unit sphere 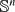as it rolls on without slipping between two points of 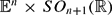. This problem is extended to situations in which an oriented sphere 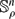of radius ρ rolls on a stationary sphere 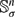and to the hyperbolic analogue in which the spheres 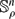and 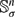are replaced by the hyperboloids 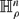and 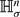respectively. The notion of “rolling” is defined in an isometric sense: the length of the path traced by the point of contact is measured by the Riemannian metric of the stationary manifold, and the orientation of the rolling object is measured by a matrix in its isometry group. These rolling problems are formulated as left invariant optimal control problems on Lie groups whose Hamiltonian extremal equations reveal two remarkable facts: on the level of Lie algebras the extremal equations of all these rolling problems are governed by a single set of equations, and the projections onto the stationary manifold of the extremal equations having I4=0, where I4 is an integral of motion, coincide with the elastic curves on this manifold. The paper then outlines some explicit solutions based on the use of symmetries and the corresponding integrals of motion.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 144 , Issue 3 , May 2008 , pp. 729 - 747
Copyright
Copyright © Cambridge Philosophical Society 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Agrachev, A. and Sarychev, Y.. Abnormal sub-Riemannian geodesics: Morse index and rigidity. Ann. Inst. H. Poincaré Anal. Non Linéaire 13 (1996), 635–690.CrossRefGoogle Scholar
[2]Agrachev, A. and Sachkov, Y.. Control Theory from the Geometric Viewpoint. Encyclopaedia of Mathematical Sciences vol. 87 (Springer–Verlag, 2004).Google Scholar
[3]M, A.. Arthurs and Walsh, G. R.. On Hammersley's Minimum Problem for a rolling sphere. Math. Proc. Camb. Phil. Soc. 99 (1986), 529–534.Google Scholar
[4]Bolsinov, A. V.. A completeness criterion for a family of functions in involution constructed by the argument shift method. Soviet Math. Dokl. 38 (1989), 161–165.Google Scholar
[5]Brockett, R. W.. and Dai, L.. Non-holonomic kinematics and the role of elliptic functions in constructive controllability. In Nonholonomic Motion Planning (Kluwer Academic, 1993), pp. 1–22.Google Scholar
[6]Bryant, R. and Griffiths, P.. Reductions for constrained variational problems and 1/2 ∞ κ2ds. Amer. J. Math. 108 (1986), 525–570.CrossRefGoogle Scholar
[7]Fomenko, A. T. and Trofimov, V. V.. Integrable Systems on Lie Algebras and Symmetric Spaces (Gordon and Breach, 1988).Google Scholar
[8]Griffiths, P.. Exterior Differential Systems and the Calculus of Variations (Birkhäuser, 1983).CrossRefGoogle Scholar
[9]Hammersley, J.. Oxford commemoration ball. In Probability, Statistics and Analysis (Cambridge University Press, 1983), 112–142.CrossRefGoogle Scholar
[10]Helgason, S.. Differential Geometry, Lie Groups and Symmetric Spaces (Academic Press, 1978)Google Scholar
[11]Jurdjevic, V.. The geometry of the plate-ball problem. Arch. Rat. Mech. Anal. 124 (1993), 305–328.CrossRefGoogle Scholar
[12]Jurdjevic, V.. Geometric Control Theory. Studies in Advanced Math. vol. 52 (Cambridge University Press, 1997).Google Scholar
[13]Jurdjevic, V. and Monroy-Perez, F.. Variational problems on Lie groups and their homogeneous spaces: elastic curves, tops, and constrained geodesic problems. In Contemporary Trends in Nonlinear Geometric Control Theory and its Applications (World Scientific, 2002), pp. 3–52.Google Scholar
[14]Jurdjevic, V.. Hamiltonian systems on complex Lie groups and their homogeneous spaces. Mem. Amer. Math. Soc. 178 (2005), no. 838.Google Scholar
[15]Langer, J. and Singer, D.. Knotted Elastic Curves in R3. J. London Math. Soc. (2) 30 (1984), 512–520.Google Scholar
[16]Moser, J.. Integrable Hamiltonian Systems and Spectral Theory. Lezioni Fermiane, Academia Nazionale dei Lincei, Scuola Normale Superiore, Pisa (1981).Google Scholar
[17]Moser, J.. Geometry of Quadrics and Spectral Theory. In The Chern Symposium 1979. Proceedings of the International Symposium on Differential Geometry held in honor of S. S. Chern (Berkeley, California, June 1979), (Springer–Verlag 1980), 147–188.Google Scholar
[18]Reyman, A. G.. Integrable Hamiltonian systems connected with graded Lie algebras. J. Sov. Math. 19 (1980), 1507–1545.Google Scholar
[19]Reyman, A. G.. and Semenov-Tian Shansky, M. A.. Group theoretic Methods in the Theory of Finite-Dimensional Integrable Systems. Dynamical Systems VII. Chapter 2. Encyclopaedia of Mathematical Sciences. vol 16 (Springer–Verlag, 1994), pp. 116–259.CrossRefGoogle Scholar
[20]Liu, W. and Sussmann, H.. Shortest paths for sub-Riemannian metrics on rank 2 distributions. Mem. Amer. Math. Soc. 118 (1995), no. 564.Google Scholar
[21]Sharpe, R. W.. Differential Geometry: Cartan's Generalization of Klein's Erlangen Program (Springer, 1997).Google Scholar
[22]Zimmerman, J.. Optimal control of the sphere Sn rolling on En. Math. Control Signals Systems 17 (2005), 14–37.CrossRefGoogle Scholar