No CrossRef data available.
Published online by Cambridge University Press: 06 September 2021
Given an infinite subset 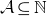 $\mathcal{A} \subseteq\mathbb{N}$
, let A denote its smallest N elements. There is a rich and growing literature on the question of whether for typical
$\mathcal{A} \subseteq\mathbb{N}$
, let A denote its smallest N elements. There is a rich and growing literature on the question of whether for typical 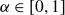 $\alpha\in[0,1]$
, the pair correlations of the set
$\alpha\in[0,1]$
, the pair correlations of the set 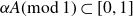 $\alpha A (\textrm{mod}\ 1)\subset [0,1]$
are asymptotically Poissonian as N increases. We define an inhomogeneous generalisation of the concept of pair correlation, and we consider the corresponding doubly metric question. Many of the results from the usual setting carry over to this new setting. Moreover, the double metricity allows us to establish some new results whose singly metric analogues are missing from the literature.
$\alpha A (\textrm{mod}\ 1)\subset [0,1]$
are asymptotically Poissonian as N increases. We define an inhomogeneous generalisation of the concept of pair correlation, and we consider the corresponding doubly metric question. Many of the results from the usual setting carry over to this new setting. Moreover, the double metricity allows us to establish some new results whose singly metric analogues are missing from the literature.
For Jorge A. Ramírez (1954–2020)—with Love and Gratitude