No CrossRef data available.
Article contents
Relations in the tautological ring derived from combinatorial classes and hyperelliptic fatgraphs
Published online by Cambridge University Press: 01 March 2008
Abstract
A closed formula is obtained for the integral 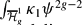 of tautological classes over the locus of hyperelliptic Weier points in the moduli space of curves. As a corollary, a relation between Hodge integrals is obtained.
of tautological classes over the locus of hyperelliptic Weier points in the moduli space of curves. As a corollary, a relation between Hodge integrals is obtained.
The calculation utilizes the homeomorphism between the moduli space of curves 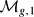 and the combinatorial moduli space
and the combinatorial moduli space  , a PL-orbifold whose cells are enumerated by fatgraphs. This cell decomposition can be used to naturally construct combinatorial PL-cycles
, a PL-orbifold whose cells are enumerated by fatgraphs. This cell decomposition can be used to naturally construct combinatorial PL-cycles 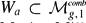 whose homology classes are essentially the Poin duals of the Mumford–Morita–Miller classes κa. In this paper we construct another PL-cycle
whose homology classes are essentially the Poin duals of the Mumford–Morita–Miller classes κa. In this paper we construct another PL-cycle 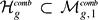 representing the locus of hyperelliptic Weier points and explicitly describe the chain level intersection of this cycle with W1. Using this description of
representing the locus of hyperelliptic Weier points and explicitly describe the chain level intersection of this cycle with W1. Using this description of 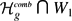 , the duality between Witten cycles Wa and the κa classes, and the Kontsevich--Penner method of integration, scheme of integrating ε classes, the integral
, the duality between Witten cycles Wa and the κa classes, and the Kontsevich--Penner method of integration, scheme of integrating ε classes, the integral 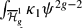 is reduced to a weighted sum over graphs and is evaluated by the enumeration of trees.
is reduced to a weighted sum over graphs and is evaluated by the enumeration of trees.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 144 , Issue 2 , March 2008 , pp. 369 - 395
- Copyright
- Copyright © Cambridge Philosophical Society 2008


