Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T02:21:49.778Z Has data issue: false hasContentIssue false
  • English
  • Français

Regulator constants of integral representations of finite groups

Published online by Cambridge University Press:  05 September 2018

ALEX TORZEWSKI
ALEX TORZEWSKI*
Affiliation:
Mathematics Institute, Zeeman Building, University of Warwick, Coventry CV4 7AL. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a finite group and p be a prime. We investigate isomorphism invariants of 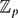$\mathbb{Z}_p$[G]-lattices whose extension of scalars to 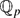$\mathbb{Q}_p$ is self-dual, called regulator constants. These were originally introduced by Dokchitser–Dokchitser in the context of elliptic curves. Regulator constants canonically yield a pairing between the space of Brauer relations for G and the subspace of the representation ring for which regulator constants are defined. For all G, we show that this pairing is never identically zero. For formal reasons, this pairing will, in general, have non-trivial kernel. But, if G has cyclic Sylow p-subgroups and we restrict to considering permutation lattices, then we show that the pairing is non-degenerate modulo the formal kernel. Using this we can show that, for certain groups, including dihedral groups of order 2p for p odd, the isomorphism class of any 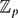$\mathbb{Z}_p$[G]-lattice whose extension of scalars to 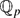$\mathbb{Q}_p$ is self-dual, is determined by its regulator constants, its extension of scalars to 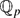$\mathbb{Q}_p$, and a cohomological invariant of Yakovlev.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 168 , Issue 1 , January 2020 , pp. 75 - 117
Copyright
Copyright © Cambridge Philosophical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported by a PhD studentship from the Engineering and Physical Sciences Research Council.

References

REFERENCES

[Bar12] Bartel, A.. On Brauer-Kuroda type relations of S-class numbers in dihedral extensions. J. Reine Angew. Math. 668 (2012), 211–244.Google Scholar
[BD14] Bartel, A. and Dokchitser, T.. Brauer relations in finite groups II: Quasi-elementary groups of order p aq. J. Group Theory 17 (2014), no. 3, 381–393.Google Scholar
[BD15] Bartel, A. and Dokchitser, T.. Brauer relations in finite groups. J. Eur. Math. Soc. 17 (2015), no. 10, 2473–2512.Google Scholar
[Beg10] Bege, A.. Generalised GCD matrices. Acta Univ. Sapientiae Math. 2 (2010), no. 2, 160–167.Google Scholar
[Ben98] Benson, D. J.. Representations and cohomology. I, second ed. Camb. Stud. Adv. Math., vol. 30 (Cambridge University Press, Cambridge, 1998). Basic representation theory of finite groups and associative algebras.Google Scholar
[Ben06] Beneish, E.. Failure of Krull-schmidt for invertible lattices over a discrete valuation ring. Proc. Amer. Math. Soc. 134 (2006), no. 7, 1869–1873.Google Scholar
[BL89] Beslin, S. and Ligh, S.. Greatest common divisor matrices. Linear Algebra Appl. 118 (1989), 69–76.Google Scholar
[CR94] Curtis, C. W. and Reiner, I.. Methods of Representation Theory Volume I (Wiley, 1994).Google Scholar
[DD09] Dokchitser, T. and Dokchitser, V.. Regulator constants and the parity conjecture. Invent. Math. 178 (2009), no. 1, 23–71.Google Scholar
[Fan91] Fan, Y.. Permutation modules, p-permutation modules and Conlon species. Sci. China Ser. A 34 (1991), no. 11, 1290–1301.Google Scholar
[HR62] Heller, A. and Reiner, I.. Representations of cyclic groups in rings of integers. I. Ann. of Math. (2) 76 (1962), 73–92.Google Scholar
[Lee64] Lee, M. P.. Integral representations of dihedral groups of order 2p. Trans. Amer. Math. Soc. 110 (1964), 213–231.Google Scholar
[Rei70] Reiner, I.. A survey of integral representation theory. Bull. Amer. Math. Soc. 76 (1970), 159–227.Google Scholar
[Sna94] Snaith, V. P.. Explicit Brauer induction. Camb. Stud. Adv. Math. vol. 40 (Cambridge University Press, Cambridge, 1994), With applications to algebra and number theory.Google Scholar
[Tor18] Torzewski, A.. Regulator constants of integral representations, together with relative motives over shimura varieties, Ph.D. thesis, University of Warwick (2018).Google Scholar
[Yak96] Yakovlev, A. V.. Homological definability of p-adic representations of groups with cyclic Sylow p-subgroup. An. Ştiinţ. Univ. Ovidius Constanţa Ser. Mat. 4 (1996), no. 2, 206–221. Representation theory of groups, algebras, and orders (Constanţa, 1995).Google Scholar