Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T05:05:01.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Rational normal octavic surfaces with a double line, in space of five dimensions

Published online by Cambridge University Press:  24 October 2008

D. W. Babbage
D. W. Babbage
Affiliation:
Magdalene College
Get access Rights & Permissions [Opens in a new window]

Extract

The following paper arises from a remark in a recent paper by Professor Baker. In that paper he gives a simple rule, under which a rational surface has a multiple line, expressed in terms of the system of plane curves which represent the prime sections of the surface. The rule is that, if one system of representing curves is given by an equation of the form

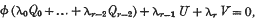
the surface being given, in space (x0, x1,…, xr), by the equations

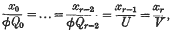
then the surface contains the line

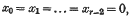
corresponding to the curve φ = 0; and if the curve φ = 0 has genus q, this line is of multiplicity q + 1.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 29 , Issue 1 , January 1933 , pp. 95 - 102
Copyright
Copyright © Cambridge Philosophical Society 1933

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Baker, , “Note in regard to surfaces in space of four dimensions, in particular rational surfaces”, Proc. Camb. Phil. Soc. 28 (1932), 77.CrossRefGoogle Scholar

* Baker, , Principles of Geometry, vol. 4, 234.Google Scholar

† The quadrics of S 5 cut out a complete system of surfaces on the locus V 34.