Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T05:40:38.330Z Has data issue: false hasContentIssue false
  • English
  • Français

Rational normal octavic surfaces with a double line, in space of five dimensions: Addition

Published online by Cambridge University Press:  24 October 2008

D. W. Babbage
D. W. Babbage
Affiliation:
Magdalene College
Get access Rights & Permissions [Opens in a new window]

Extract

In a recent paper in these Proceedings on the rational normal octavic surfaces with a double line in [5] I found four such surfaces, 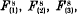, and 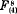representable on a plane respectively by the systems of curves C5 (22, 19), C6(26, 14), and C7 (3, 28), with the base points in each case lying on an elliptic cubic. Inadvertently I overlooked a solution of certain indeterminate equations which leads to a fifth type 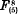represented by the plane system C9(38, 1).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 29 , Issue 3 , 30 July 1933 , pp. 405 - 406
Copyright
Copyright © Cambridge Philosophical Society 1933

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Babbage, , “Rational normal octavic surfaces with a double line, in space of five dimensions”, Proc. Camb. Phil. Soc., 29 (1933), 95–102.CrossRefGoogle Scholar

† Roth, , “On surfaces of sectional genus four”, Proc. Camb. Phil. Soc., 29 (1933), 184–194.CrossRefGoogle Scholar