Hostname: page-component-6bf8c574d5-w79xw Total loading time: 0 Render date: 2025-02-22T23:39:01.916Z Has data issue: false hasContentIssue false
  • English
  • Français

Ramsey numbers of hypergraphs with a given size

Part of: Extremal combinatorics

Published online by Cambridge University Press:  13 January 2025

DOMAGOJ BRADAČ ,
JACOB FOX  and
BENNY SUDAKOV
DOMAGOJ BRADAČ
Affiliation:
Department of Mathematics, ETH, Zürich, Switzerland. e-mail: [email protected]
JACOB FOX
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA, U.S.A. e-mail: [email protected]
BENNY SUDAKOV
Affiliation:
Department of Mathematics, ETH, Zürich, Switzerland. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The q-colour Ramsey number of a k-uniform hypergraph H is the minimum integer N such that any q-colouring of the complete k-uniform hypergraph on N vertices contains a monochromatic copy of H. The study of these numbers is one of the central topics in Combinatorics. In 1973, Erdős and Graham asked to maximise the Ramsey number of a graph as a function of the number of its edges. Motivated by this problem, we study the analogous question for hypergaphs. For fixed 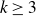$k \ge 3$ and $q \ge 2$ we prove that the largest possible q-colour Ramsey number of a k-uniform hypergraph with m edges is at most 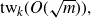$\mathrm{tw}_k(O(\sqrt{m})),$ where tw denotes the tower function. We also present a construction showing that this bound is tight for $q \ge 4$. This resolves a problem by Conlon, Fox and Sudakov. They previously proved the upper bound for 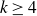$k \geq 4$ and the lower bound for 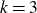$k=3$. Although in the graph case the tightness follows simply by considering a clique of appropriate size, for higher uniformities the construction is rather involved and is obtained by using paths in expander graphs.

MSC classification

Primary: 05D10: Ramsey theory
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , First View , pp. 1 - 14
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research supported in part by SNSF grant 200021-228014.

‡

Research supported by NSF Awards DMS-1953990 and DMS-2154129.

References

Burr, S. A. and Erdős, P.. On the magnitude of generalized Ramsey numbers for graphs. In Infinite and finite sets, vols. I, II, III. Colloq. Math. Soc. János Bolyai, vol. 10, (North-Holland, Amsterdam, 1975), pp. 215–240.Google Scholar
Campos, M., Griffiths, S., Morris, R. and Sahasrabudhe, J.. An exponential improvement for diagonal Ramsey. ArXiv :2303.09521 (2023).Google Scholar
Chvatál, C., Rödl, V., Szemerédi, E. and Trotter, W. T., Jr. The Ramsey number of a graph with bounded maximum degree. J. Combin. Theory Ser. B 34(3) (1983), 239–243.CrossRefGoogle Scholar
Conlon, D., Fox, J. and Sudakov, B.. Ramsey numbers of sparse hypergraphs. Random Structures Algorithms 35(1) (2009), 1–14.CrossRefGoogle Scholar
Conlon, D., Fox, J. and Sudakov, B.. Recent developments in graph Ramsey theory. Surveys in Combinatorics 424(2015) (2015), 49–118.Google Scholar
Conlon, David, Fox, Jacob and Sudakov, Benny. On two problems in graph Ramsey theory. Combinatorica 32(5) (2012), 513–535.CrossRefGoogle Scholar
Cooley, O., Fountoulakis, N., Kühn, D. and Osthus, D.. Embeddings and Ramsey numbers of sparse $\kappa$ -uniform hypergraphs. Combinatorica 29 (2009), 263–297.CrossRefGoogle Scholar
Erdős, P.. Some remarks on the theory of graphs. Bull. Amer. Math. Soc. 53 (1947), 292–294.CrossRefGoogle Scholar
Erdős, P.. On extremal problems of graphs and generalized graphs. Israel J. Math. 2 (1964), 183–190.CrossRefGoogle Scholar
Erdős, P.. On some problems in graph theory, combinatorial analysis and combinatorial number theory. In Graph Theory and Combinatorics (Cambridge, 1983), (Academic Press, London, 1984), pp. 1–17.Google Scholar
Erdős, P. and Graham, R. L.. On partition theorems for finite graphs. In Infinite and finite sets, Vols. I, II, III, Colloq. Math. Soc. János Bolyai, Vol. 10, pages 515–527. North-Holland, Amsterdam, 1975.Google Scholar
Erdős, P., Hajnal, A. and Rado, R.. Partition relations for cardinal numbers. Acta Math. Acad. Sci. Hungar. 16 (1965), 93–196.CrossRefGoogle Scholar
Erdős, P. and Rado, R.. Combinatorial theorems on classifications of subsets of a given set. Proc. London Math. Soc. (3). 2 (1952), 417–439.Google Scholar
Erdős, P. and Szekeres, G.. A combinatorial problem in geometry. Compositio Math. 2 (1935), 463–470.Google Scholar
Fox, J. and Sudakov, B.. Density theorems for bipartite graphs and related Ramsey-type results. Combinatorica 29 (2009), 153–196.CrossRefGoogle Scholar
Graham, R. L., Rődl, V. and Ruciński, A.. On graphs with linear Ramsey numbers. J. Graph Theory 35(3) (2000), 176–192.3.0.CO;2-C>CrossRefGoogle Scholar
Graham, R. L., Rothschild, B. L. and Spencer, J. H.. Ramsey Theory, vol. 20 (John Wiley & Sons, 1991).Google Scholar
Janson, S., Rucinski, A., and T. Łuczak. Random Graphs (John Wiley & Sons, 2011).Google Scholar
Kővári, P., Sós, V. T. and Turán, P.. On a problem of Zarankiewicz. In Colloq. Math. vol. 3 (Polska Akademia Nauk, 1954), pp. 50–57.CrossRefGoogle Scholar
Lee, C.. Ramsey numbers of degenerate graphs. Ann. of Math., 185(3) (2017), 791–829.CrossRefGoogle Scholar
Ramsey, F. P.. On a problem of formal logic. Proc. London Math. Soc. s2-30(1) (1930), 264–286.CrossRefGoogle Scholar
Sudakov, B.. A conjecture of Erdős on graph Ramsey numbers. Adv. Math. 227(1) (2011), 601–609.CrossRefGoogle Scholar