Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Friedlander, F.G
2001.
Notes on the Wave Equation on Asymptotically Euclidean Manifolds.
Journal of Functional Analysis,
Vol. 184,
Issue. 1,
p.
1.
Sá Barreto, Antônio
2003.
Radiation Fields on Asymptotically Euclidean Manifolds.
Communications in Partial Differential Equations,
Vol. 28,
Issue. 9-10,
p.
1661.
MASON, LIONEL J.
and
NICOLAS, JEAN-PHILIPPE
2004.
CONFORMAL SCATTERING AND THE GOURSAT PROBLEM.
Journal of Hyperbolic Differential Equations,
Vol. 01,
Issue. 02,
p.
197.
Sá Barreto, Antônio
2005.
Radiation fields, scattering, and inverse scattering on asymptotically hyperbolic manifolds.
Duke Mathematical Journal,
Vol. 129,
Issue. 3,
Finch, David
and
Rakesh
2005.
Trace identities for solutions of the wave equation with initial data supported in a ball.
Mathematical Methods in the Applied Sciences,
Vol. 28,
Issue. 16,
p.
1897.
Mason, Lionel J.
and
Nicolas, Jean-Philippe
2009.
Regularity at space-like and null infinity.
Journal of the Institute of Mathematics of Jussieu,
Vol. 8,
Issue. 1,
p.
179.
Katayama, Soichiro
and
Kubo, Hideo
2010.
The Rate of Convergence to the Asymptotics for the Wave Equation in an Exterior Domain.
Funkcialaj Ekvacioj,
Vol. 53,
Issue. 3,
p.
331.
Vasy, András
2010.
The wave equation on asymptotically de Sitter-like spaces.
Advances in Mathematics,
Vol. 223,
Issue. 1,
p.
49.
JOUDIOUX, JÉRÉMIE
2012.
CONFORMAL SCATTERING FOR A NONLINEAR WAVE EQUATION.
Journal of Hyperbolic Differential Equations,
Vol. 09,
Issue. 01,
p.
1.
Vasy, András
2013.
Microlocal analysis of asymptotically hyperbolic and Kerr-de Sitter spaces (with an appendix by Semyon Dyatlov).
Inventiones mathematicae,
Vol. 194,
Issue. 2,
p.
381.
Melrose, Richard
Barreto, AntÔnio Sá
and
Vasy, András
2014.
Asymptotics of Solutions of the Wave Equation on de Sitter-Schwarzschild Space.
Communications in Partial Differential Equations,
Vol. 39,
Issue. 3,
p.
512.
Baskin, Dean
and
Wang, Fang
2014.
Radiation Fields on Schwarzschild Spacetime.
Communications in Mathematical Physics,
Vol. 331,
Issue. 2,
p.
477.
Baskin, Dean
2014.
Equipartition of energy in geometric scattering theory.
Journal d'Analyse Mathématique,
Vol. 123,
Issue. 1,
p.
341.
Alexakis, Spyros
and
Shao, Arick
2015.
Global uniqueness theorems for linear and nonlinear waves.
Journal of Functional Analysis,
Vol. 269,
Issue. 11,
p.
3458.
Hora, Raphael
and
Barreto, Antônio
2015.
Inverse scattering with partial data on asymptotically hyperbolic manifolds.
Analysis & PDE,
Vol. 8,
Issue. 3,
p.
513.
Baskin, Dean
and
Sá Barreto, Antônio
2015.
Radiation fields for semilinear wave equations.
Transactions of the American Mathematical Society,
Vol. 367,
Issue. 6,
p.
3873.
Sá Barreto, Antônio
2016.
A local support theorem for the radiation fields on asymptotically euclidean manifolds.
Journal d'Analyse Mathématique,
Vol. 130,
Issue. 1,
p.
275.
Nicolas, Jean-Philippe
2017.
From Riemann to Differential Geometry and Relativity.
p.
571.
Drouot, Alexis
2017.
A Quantitative Version of Hawking Radiation.
Annales Henri Poincaré,
Vol. 18,
Issue. 3,
p.
757.
Baskin, Dean
Vasy, András
and
Wunsch, Jared
2018.
Asymptotics of scalar waves on long-range asymptotically Minkowski spaces.
Advances in Mathematics,
Vol. 328,
Issue. ,
p.
160.
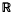 3, t ∈
3, t ∈ 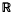 , be a C∞ solution of the wave equation on {|x| > a} ×
, be a C∞ solution of the wave equation on {|x| > a} ×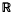 for some a > 0, and suppose that u = 0 for |x|> a, t < 0. One then also has u = 0 for |x| > a + t, t > 0, so that u(.,t) can be thought of as a wave expanding into a previously undisturbed medium. One can now ask for a description of the asymptotic behaviour of u as |x| → ∞. It turns out that there is a v0(θ, τ) ∈ C∞ (S2 ×
for some a > 0, and suppose that u = 0 for |x|> a, t < 0. One then also has u = 0 for |x| > a + t, t > 0, so that u(.,t) can be thought of as a wave expanding into a previously undisturbed medium. One can now ask for a description of the asymptotic behaviour of u as |x| → ∞. It turns out that there is a v0(θ, τ) ∈ C∞ (S2 × 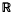 ) such that
) such that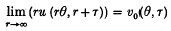
 ). This limit may be called the radiation field of the expanding wave u. (See (2) and the earlier papers quoted there.)
). This limit may be called the radiation field of the expanding wave u. (See (2) and the earlier papers quoted there.)

