Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T15:14:46.933Z Has data issue: false hasContentIssue false
  • English
  • Français

Quantum SO(3)-invariants dominate the SU(2)-invariant of Casson and Walker

Published online by Cambridge University Press:  24 October 2008

Hitoshi Murakami
Hitoshi Murakami
Affiliation:
Department of Mathematics, Osaka City university, Sugimoto, Sumiyoshi-ku, Osaka 558, Japan, E-mail address: [email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

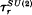For a compact Lie group G, E. Witten proposed topological invariants of a threemanifold (quantum G-invariants) in 1988 by using the Chern-Simons functional and the Feynman path integral [30]. See also [2]. N. Yu. Reshetikhin and V. G. Turaev gave a mathematical proof of existence of such invariants for G = SU(2) [28]. R. Kirby and P. Melvin found that the quantum SU(2)-invariant associated to q = exp(2π √ − 1/r) with r odd splits into the product of the quantum SO(3)-invariant 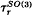and 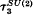[15]. For other approaches to these invariants, see [3, 4, 5, 16, 22, 27].

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 117 , Issue 2 , March 1995 , pp. 237 - 249
Copyright
Copyright © Cambridge Philosophical Society 1995

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Akbulut, S. and McCarthy, J. D.. Casson's Invariant for Oriented Homology 3-spheres – An Exposition. Mathematical Notes 36 (Princeton Univ. Press, 1990).CrossRefGoogle Scholar
[2]Atiyah, M.. The Geometry and Physics of Knots (Cambridge Univ. Press, 1990).CrossRefGoogle Scholar
[3]Blanchet, C.. Invariant of three-manifolds with spin structure. Comment. Math. Helv. 67 (1992), 406–427.CrossRefGoogle Scholar
[4]Blanchet, C., Habegger, N., Masbaum, G. and Vogel, P.. Three-manifold invariants derived from the Kauffman bracket. Topology 31 (1992), 685–699.CrossRefGoogle Scholar
[5]Blanchet, C., Habegger, N., Masbaum, G. and Vogel, P.. Topological quantum field theories derived from the Kauffman bracket (preprint), Université de Nantes, 1993.CrossRefGoogle Scholar
[6]Conway, J. H.. An enumeration of knots and links, and some of their algebraic properties. Computational Problems in Abstract Algebra (Pergamon Press, 1969), pp. 329–358.Google Scholar
[7]Hoste, J.. A formula for Casson's invariant. Trans. Amer. Math. Soc. 297 (1986), 547–562.Google Scholar
[8]Ireland, K. and Rosen, M.. A Classical Introduction to Modern Number Theory, Second Edition, Graduate Texts in Math. 84 (Springer, 1990).CrossRefGoogle Scholar
[9]Ishibe, K.. A Dehn surgery formula for Walker invariant on a link (preprint). Tokyo Metropolitan Univ.CrossRefGoogle Scholar
[10]Jones, V. F. R.. A polynomial invariant for knots via von Neumann algebras. Bull. Amer. Math. Soc. (N.S.) 12 (1985), 103–111.CrossRefGoogle Scholar
[11]Jones, V. F. R.. Hecke algebra representations of braid groups and link polynomials. Ann. of Math. 126 (1987), 335–388.CrossRefGoogle Scholar
[12]Kauffman, L. H.. The Conway polynomial. Topology 20 (1981), 101–108.CrossRefGoogle Scholar
[13]Kawauchi, A. and Kojima, S.. Algebraic classification of linking pairings on 3-manifolds. Math. Ann. 253 (1980), 29–42.CrossRefGoogle Scholar
[14] R. Kirby, C.. A calculus for framed links in S 3. Invent. Math. 45 (1978), 35–56.CrossRefGoogle Scholar
[15]Kirby, R. and Melvin, P.. The 3-manifold invariants of Witten and Reshetikhin-Turaev for sl(2, ℂ). Invent. Math. 105 (1991), 473–545.CrossRefGoogle Scholar
[16]Kohno, T.. Topological invariants for 3-manifolds using representations of mapping class groups I. Topology 31 (1992), 203–230.CrossRefGoogle Scholar
[17]Kneser, M. and Puppe, P.. Quadratische Formen und Verschlingungsinvarianten von Knoten. Math. Z. 58 (1953), 376–384.CrossRefGoogle Scholar
[18]Kyle, R. H.. Branched covering spaces and the quadratic forms of links. Ann. of Math. 59 (1954), 539–548.CrossRefGoogle Scholar
[19]Lescop, C.. Global surgery formula for the Casson-Walker invariant (preprint). Ecole Normale Supérieure de Lyon, 1993.Google Scholar
[20]Lickorish, W. B. R.. A representation of orientable combinatorial 3-manifolds. Ann. of Math. 76 (1962), 531–540.CrossRefGoogle Scholar
[21]Lickorish, W. B. R.. Calculations with the Temperley-Lieb algebra. Comment. Math. Helv. 67 (1992), 571–591.CrossRefGoogle Scholar
[22]Lickorish, W. B. R.. The skein method for three-manifold invariants. J. Knot Theory Ramifications 1 (1993), 171–194.CrossRefGoogle Scholar
[23]Murakami, H.. Quantum SU(2)-invariants dominate Casson's SU(2)-invariant. Math. Proc. Cambridge Philos. Soc. (to appear).Google Scholar
[24]Murakami, H., Ohtsuki, T. and Okada, M.. Invariants of three-manifolds derived from linking matrices of framed links. Osaka J. Math. 29 (1992), 545–572.Google Scholar
[25]Ohtsuki, T.. A polynomial invariant of integral homology spheres (preprint). Univ. of Tokyo, 1993.Google Scholar
[26]Ohtsuki, T.. A Polynomial invariant of rational homology spheres (preprint). Univ. of Tokyo, 1993.Google Scholar
[27]Piunikhin, S.. Reshetikhin-Turaev and Crane-Kohno-Kontsevich 3-manifold invariants coincide. J. Knot Theory Ramifications 2 (1993), 65–95.CrossRefGoogle Scholar
[28]Reshetikhin, N. Yu. and Turaev, V. G.. Invariants of 3-manifolds via link polynomials and quantum groups. Invent. Math. 103 (1991), 547–597.CrossRefGoogle Scholar
[29]Walker, K.. An Extension of Casson's Invariant. Ann. of Math. Stud. 126 (Princeton Univ. Press, 1992).CrossRefGoogle Scholar
[30]Witten, E.. Quantum field theory and the Jones polynomial. Comm. Math. Phys. 121 (1989), 351–399.CrossRefGoogle Scholar