The Pure Archimedean Polytopes in Six and Seven Dimensions
Published online by Cambridge University Press: 24 October 2008
Extract
An Archimedean solid (in three dimensions) may be defined as a polyhedron whose faces are regular polygons of two or more kinds and whose vertices are all surrounded in the same way. For example, the “great rhombicosidodecahedron” is bounded by squares, hexagons and decagons, one of each occurring at each vertex. Thus any Archimedean solid is determined by the faces which meet at one vertex, and therefore by the shape and size of the “vertex figure,” which may be defined as follows. Suppose, for simplicity, that the length of each edge of the solid is unity. The further extremities of all the edges which meet at a particular vertex lie on a sphere of unit radius, and also on the circumscribing sphere of the solid, and therefore on a circle. These points form a polygon, called the “vertex figure,” whose sides correspond to the faces at a vertex and are of length 2 cos π/n for an n-gonal face. Thus the vertex figure of the great rhombicosi-dodecahedron is a scalene triangle of sides 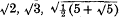 .
.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 24 , Issue 1 , January 1928 , pp. 1 - 9
- Copyright
- Copyright © Cambridge Philosophical Society 1928
References
* Cf. Baker, , Principles of Geometry, vol. 4 (1925), p. 104.Google Scholar
† See, for instance, Segre's report, Encyl. math. Wiss., III, c7, p. 805.Google Scholar
* For the configuration of the 27 lines see Baker, , Principles of Geometry, vol. 3 (1923), p. 166.Google Scholar
† Schoute, P. H., Proc. Roy. Acad. Sci., Amsterdam, 24 09, 1910, pp. 375–383.Google ScholarFurther references are given in Baker, , Principles of Geometry, vol. 4 (1925), p. 105.Google Scholar
- 14
- Cited by


