Pseudoprime Reductions of Elliptic Curves – CORRIGENDUM

Extract

Unfortunately, there are two inaccuracies in the argument of [CLS]. First, the statements of Lemmas 3, 4, 6, and 7 of [CLS] hold only under the additional condition gcd(m, M_E) = 1 for some integer M_E ≥ 1 depending only on E. Second, the divisibility condition (3·6) in [CLS] implies that t_b(ℓ) | n_E(p)−1 (rather than t_b(ℓ) | n_E(p), as it was erroneously claimed on p. 519 in [CLS]). In particular, instead of the divisibility ℓt_b(ℓ) | n_E(p) (see the last displayed formula on p. 519 in [CLS]), we conclude that for every prime ℓ | L there is an integer a_ℓ such that(0.1)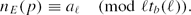However, the final result is correct and can easily be recovered. To do so, we remark that under the condition gcd(m,M_E) =1, we have full analogues of Lemmas 6, 7, 9, and 10 of [CLS] for the function Π(x;m,a) defined as the number of primes p ≤ x with n_E(p) ≡ a (mod m) (rather than just for Π(x;m) = Π(x;m,0) as in [CLS]). Define ρ*(n) as the largest square-free divisor of n which is relatively prime to M_E. We then derive from (0.1) above that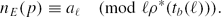Therefore(0.2)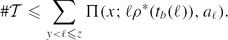Sincewe see that (0.2) above implies the bound (3·7) from [CLS], and the result now follows without any further changes.