Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T13:41:26.678Z Has data issue: false hasContentIssue false
  • English
  • Français

Proof of the antithetic-variates theorem for unbounded functions

Published online by Cambridge University Press:  24 October 2008

James R. Wilson
James R. Wilson
Affiliation:
Purdue University, Indiana 47907, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

The method of antithetic variates introduced by Hammersley and Morton (2) is one of the most widely used Monte Carlo techniques for estimating an unknown parameter θ. The basis for this method was established by Hammersley and Mauldon(l).in the case of unbiased estimators with the form

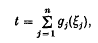
where each of the variates ξj is required to have a uniform marginal distribution over the unit interval [0,1]. By assuming that n = 2 and that the gj are bounded Borel functions, Hammersley and Mauldon showed that the greatest lower bound of var (t) over all admissible joint distributions for the variates ξj can be approached simply by arranging an appropriate strict functional dependence between the ξj. Handscomb(3) extended this result to the case of n > 2 bounded antithetic variates gj(ξj). In many experiments involving distribution sampling or the simulation of some stochastic process over time, the response functions gry are unbounded. This paper further extends the antithetic-variates theorem to include the case of n ≥ 2 unbounded antithetic variates gj(ξj) each with finite variance.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 86 , Issue 3 , November 1979 , pp. 477 - 479
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Hammersley, J. M. and Mauldon, J. G.General principles of antithetic variates. Proc. Cambridge Philos. Soc. 52 (1956), 476–481.CrossRefGoogle Scholar
(2)Hammersley, J. M. and Morton, K. W.A new Monte Carlo technique: antithetic variates. Proc. Cambridge Philos. Soc. 52 (1956), 449–475.CrossRefGoogle Scholar
(3)Handscomb, D. C.Proof of the antithetic-variates theorem for n > 2. Proc. Cambridge Philos. Soc. 54 (1958), 300–301.CrossRefGoogle Scholar