Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T01:13:50.751Z Has data issue: false hasContentIssue false
  • English
  • Français

Projective actions, invariant sigma-curves and quadratic functional equations

Published online by Cambridge University Press:  24 October 2008

Patrick J. McCarthy
Patrick J. McCarthy
Affiliation:
School of Mathematical Sciences, Queen Mary College, London E1 4NS
Get access Rights & Permissions [Opens in a new window]

Abstract

The quadratic functional equation f(f(x)) *–Tf(x) + Dx = 0 is equivalent to the requirement that the graph 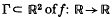be invariant under a certain linear map 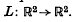The induced projective map is used to show that the equation admits a rich supply of continuous solutions only when L is hyperbolic (T2 > 4D), and then only when T and D satisfy certain further conditions. The general continuous solution of the equation is given explicitly in terms of either (a) an expression involving an arbitrary periodic function, function additions, inverses and composites, or(b) suitable limits of such solutions.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 98 , Issue 2 , September 1985 , pp. 195 - 212
Copyright
Copyright © Cambridge Philosophical Society 1985

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]McCarthy, P. J.. Functional nth roots of unity. Math. Gaz. 64 (1980), 107–115.CrossRefGoogle Scholar
[2]McCarthy, P. J., Crampin, M. and Stephenson, W.. Graphs in the plane invariant under an area preserving map and general continuous solutions of certain quadratic functional equations. Math. Proc. Cambridge Philos. Soc. 97 (1985), 261–278.CrossRefGoogle Scholar
[3]McCarthy, P. J. and Stephenson, W.. Proc. London Math. Soc. (in the Press).Google Scholar
[4]McCarthy, P. J.. The general exact bijective continuous solution of Feigenbaum's functional equation. Comm. Math. Phys. 91 (1983), 431–443.CrossRefGoogle Scholar