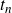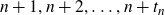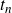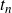A problem of Erdős–Graham–Granville–Selfridge on integral points on hyperelliptic curves

Abstract

Erdős, Graham and Selfridge considered, for each positive integer n, the least value of $t_n$ so that the integers $n+1, n+2, \dots, n+t_n $ contain a subset the product of whose members with n is a square. An open problem posed by Granville concerns the size of $t_n$, under the assumption of the ABC conjecture. We establish some results on the distribution of $t_n$, and in the process solve Granville’s problem unconditionally.

1. Introduction

A question of Erdős, Graham and Selfridge ([6] and [9, B30]) asks to find the least value of $t_n$ so that the integers $n+1, n+2, \dots, n+t_n $ contain a subset the product of whose members with n is a square. (If n is a square then we set $t_n=0$ .) That is, $t_n \geq 0$ is the least integer such that there are integers $1\leq j_1 < \cdots <j_s = t_n$ with

\begin{align*}n\prod_{i=1}^s (n+j_i) = \square,\end{align*}

where “ $m = \square$ ” means that the integer m is a square. For instance, we easily compute that $t_2 = 4, t_3 = 5$ and $t_5 = 5$ , since

\begin{align*}2\cdot 3\cdot 6 &= 6^2,\\ 3 \cdot 6 \cdot 8 &= 12^2,\\ 5 \cdot 8 \cdot 10 &= 20^2,\end{align*}

and none of the last numbers in the products can be replaced by smaller integers.

One can interpret $t_n$ in terms of integer points on hyperelliptic curves. As an example, we have $t_{14}=7$ from $14\cdot 15 \cdot 18\cdot 20\cdot 21=1260^2$ , and this gives rise to the integral point $(x,y)=(14,1260)$ on the hyperelliptic curve $y^2=x(x+1)(x+4)(x+6)(x+7)$ . Granville noted this connection [9, B30] and observed that effective versions of Faltings’ Theorem [7] would lead to corresponding effective bounds on $t_n$ . Granville mentioned that the ABC conjecture should lead, via work of Elkies [4] and Langevin [12], to stronger bounds on $t_n$ . He also stated that, presumably, $t_n > n^c $ for some fixed constant $ c > 0 $ , and perhaps one could prove this assuming the ABC conjecture.

Our first result below shows that this supposition fails dramatically. A beautiful result of Granville and Selfridge [8, Corollary 1] shows that if the largest prime factor $P^+(n) $ of n satisfies $P^+(n) > \sqrt{2n}+1$ then $t_n = P^+(n)$ . This inspired us to study closely the relationship between $P^+(n)$ and $t_n$ . While $t_n$ and $P^+(n)$ may no longer be close if $P^+(n) \leq \sqrt{2n}+1$ , we find the distribution of $t_n$ continues to follow that of $P^+(n)$ in larger ranges.

Theorem 1·1. For any fixed $c \in (0,1]$ ,

$$\lim_{x\to\infty} \frac{ \#\{ n \le x \;:\; t_n \leq n^c \} }{x} = \lim_{x\to\infty} \frac{ \#\{ n \le x \;:\; P^+(n) \leq n^c \} }{x} \; .$$

Remark 1. The right-hand side in the statement of Theorem 1·1 is equal to $\rho(1/c)$ , where $\rho(u)$ is the well-known Dickman–de Bruijn function which plays a prominent role in the theory of smooth numbers [11]. Therefore, for every fixed $c > 0$ a positive proportion of integers n satisfy $t_n \leq n^c$ .

Theorem 1·1 is a corollary of a slightly stronger theorem (Theorem 3·1) which we state and prove in Section 3 below.

Our next result shows there are integers n attaining even smaller values of $t_n$ , much smaller than $n^c$ .

Theorem 1·2. Let $\epsilon>0$ be fixed and sufficiently small, and let x be sufficiently large depending on $\epsilon$ . Then there are at least $x \exp\! \Big(\!-\!\big({3\sqrt{2}}/{2}+\epsilon \big)\sqrt{\log x \log \log x} \Big)$ integers $n\leq x$ such that $t_n \leq \exp\! \left(\sqrt{(2+\epsilon)\log n \log \log n} \right)$ .

Suitable modification of the proof of Theorem 1·2 shows there exist hyperelliptic curves of large genus which have integral points of nontrivial height (see further comments and discussion at the end of Section 5).

Theorem 1·3. Fix a constant $c \in (0,1)$ . There are arbitrarily large positive integers J such that the following is true: there exist N positive integers $1\leq j_1 < j_2 < \cdots < j_N < J$ with $N \geq J^{1-c}$ and a positive integer $x\geq \exp\! \left({c^2}{(\!\log J)^2}/({5\log \log J}) \right)$ such that $x(x+J)\prod_{i=1}^N(x+j_i)$ is a square.

In the complementary direction, we prove a lower bound on $t_n$ when n is not a square (recall $t_n=0$ when n is a square). The proof also uses a framework of hyperelliptic curves, and requires bounding the height of integral points on curves.

Theorem 1·4. If n is a sufficiently large non-square integer, then

\begin{align*}t_n \gg (\!\log \log n)^{6/5}(\!\log \log \log n)^{-1/5}.\end{align*}

The implied constant is effectively computable.

The outline of the rest of the paper is as follows. In Section 2, we describe the notation and conventions of the paper. In Section 3, we state Theorem 3·1, of which Theorem 1·1 is essentially a special case; we assemble the ingredients for the proof and then prove Theorems 3·1 and 1·1. In Section 4, we prove Theorem 1·2. Section 5 contains the results and modifications of the proof of Theorem 1·2 necessary to prove Theorem 1·3; we close the section with some comments and discussion. We prove Theorem 1·4 in Section 6.

2. Notation and conventions

Given a positive integer n, the integer $t_n$ is the smallest nonnegative integer so that the integers $n+1, n+2, \dots, n+t_n $ contain a subset the product of whose members with n is a square. If n is a square then we define $t_n=0$ .

The expression $m = \square$ means that the integer m is a square. We write $P^+(n)$ for the largest prime factor of a positive integer n. We set $P^+(1)=1$ . We write $\omega(n)$ for the number of distinct prime factors of n.

A number n is y–smooth if $P^+(n)\leq y$ . We write $\Psi(x,y)$ for the number of y–smooth integers $n\leq x$ , and $\rho(u)$ for the Dickman–de Bruijn function.

We let $P^*(n)$ denote the largest prime which divides n to an odd power. Let $S_\square(x,y) = \{n\leq x \;:\; P^*(n)\leq y\}$ , the set of integers $n\leq x$ which are a square times a y–smooth integer. As noted by Granville and Selfridge [8, p.4] we have $P^*(n)\leq t_n$ . Therefore, if $n\leq x$ and $t_n\leq y$ , then $n \in S_\square(x,y)$ . So

\begin{align*}\#\{n\leq x \;:\; t_n \leq y\} \leq |S_\square(x,y)| \;=\!:\; \Psi_\square(x,y).\end{align*}

One can easily show that $\Psi_\square(x,y) \sim \Psi(x,y)$ for $y\geq (\!\log x)^3$ by results on $\Psi(x/d,y)/\Psi(x,y)$ like in [3].

Given two finite sets S and T, we write $S \Delta T$ for the symmetric difference of S and T. That is, $S\Delta T$ consists of those elements which are in one of S or T but not both: $S\Delta T = (S \cup T) \backslash (S \cap T)$ . By associativity one can consider the symmetric difference of any finite number of sets

\begin{align*}S_1 \Delta S_2 \Delta \cdots \Delta S_k = \{x \;:\; x \text{ is an element of an odd number of the sets }S_i\}.\end{align*}

Given a finite set S we write $\# S$ or $|S|$ for the cardinality of S. The power set of S, i.e. the set that consists of all the subsets of S, is denoted by $\mathcal{P}(S)$ .

The finite field with two elements is denoted as $\mathbb{F}_2$ .

The real number x is always large. The notation o(1) denotes a quantity tending to zero as some other parameter, usually x, tends to infinity. We write $f \ll g, g \gg f$ , or $f = O(g)$ if there exists a constant C such that $f \leq Cg$ . We write $f \sim g$ if $f = (1+o(1))g$ .

In discussion, but not in proofs, we sometimes refer to the height of an integral point (x, y) on a curve. By this we mean the naive height $\max(|x|,|y|)$ . We similarly refer to the height of an integer polynomial, which is the maximum of the absolute value of its coefficients.

3. The distribution of $t_n$ : Proof of Theorem 1·1

As mentioned in the introduction, Theorem 1·1 is a corollary of a somewhat stronger result, which we state here.

Theorem 3·1. Let x be sufficiently large, and let c satisfy ${(\!\log \log \log x)^2}/{\log \log x} \leq c \leq 1$ . Then

\begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}}1 = \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}} 1 + O \Big(\frac{x}{c\log x} \Big)\end{align*}

uniformly in c.

We prove Theorem 3·1 by proving upper bounds for

\begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}}1 \ \ \ \ \ \ \ \text{ and } \ \ \ \ \ \ \ \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}}1\end{align*}

in terms of each other. More precisely, the proof of Theorem 3·1 relies on the following two propositions.

Proposition 3·2 ( $t_n$ less than $P^+(n)$ on average). Let $0 < c \leq 1$ . Then

\begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}}1 \leq \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}}1 + O(x\exp\!(\!-\!\sqrt{\log x}))\end{align*}

uniformly in c.

Proposition 3·3 ( $P^+(n)$ less than $t_n$ on average). Let $0 < c \leq 1$ . Then

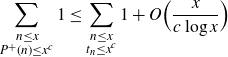\begin{align*}\sum_{\substack{n\leq x \\ P^+(n) \leq x^c}}1 \leq \sum_{\substack{n\leq x \\ t_n \leq x^c}}1 + O \Big(\frac{x}{c\log x} \Big)\end{align*}

uniformly in c.

Proof of Theorem 3·1 assuming Propositions 3·2 and 3·3. From Proposition 3·2 we have

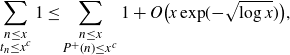\begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}}1 \leq \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}}1 + O\big(x\exp\!(\!-\!\sqrt{\log x})\big),\end{align*}

so from Proposition 3·3 we have

\begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}}1 = \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}}1 + O \Big(\frac{x}{c\log x} \Big).\end{align*}

That this asymptotic formula is non-trivial for the stated range of c follows from classical estimates for smooth numbers [10, 11].

We first turn our attention to Proposition 3·2, since the proof is simpler and introduces some of the key ideas. The first result we need is a simple inequality relating $t_n$ and $P^+(n)$ .

Lemma 3·4. If $P^+(n)^2 \nmid n$ , then $t_n \geq P^+(n)$ .

Proof. Let $p = P^+(n)$ . If $p^2 \nmid n$ , then n is not a square so by the definition of $t_n$ there are integers $1\leq j_1 < \cdots < j_s =t_n$ with $n\prod_{i=1}^s (n+j_i) = \square$ . Since p divides the left-hand side to an even power but $p^2 \nmid n$ there is some i such that $p \mid n+j_i$ . Since $p\mid n$ and $p \mid n+j_i$ we have $p \mid j_i$ , so $t_n \geq j_i \geq p$ .

We also need a result quantifying that it is rare for an integer n to be divisible by the square of its largest prime factor (see also [5, p. 345]).

Lemma 3·5 (Bound for exceptional set with $P^+(n)^2 \mid n$ ). Let $\mathcal{E}$ denote the set of $n\leq x$ such that $P^+(n)^2 \mid n$ . Then $|\mathcal{E}| \ll x \exp\!(\!-\!\sqrt{\log x})$ .

Proof. Any $n \in \mathcal{E}$ may be written as $n = p^2 m$ , where $P^+(m) \leq p$ , and therefore

\begin{align*}|\mathcal{E}| &\leq \sum_{p\leq x^{1/2}} \sum_{\substack{m\leq x/p^2 \\ P^+(m) \leq p}} 1.\end{align*}

We introduce a parameter $10\leq P \leq x^{1/2}$ and split the sum over p at P. The contribution from $p > P$ is trivially $\ll x/P$ . We bound the contribution from $p\leq P$ using Rankin’s trick. Set $\alpha = 1 - {1}/{\log P}$ , so that

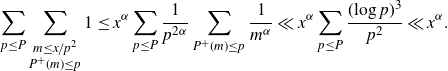\begin{align*}\sum_{p\leq P}\sum_{\substack{m\leq x/p^2 \\ P^+(m) \leq p}} 1 &\leq x^{\alpha}\sum_{p\leq P} \frac{1}{p^{2\alpha}} \sum_{P^+(m) \leq p} \frac{1}{m^\alpha} \ll x^\alpha \sum_{p\leq P} \frac{(\!\log p)^3}{p^2} \ll x^\alpha.\end{align*}

We have therefore proved $|\mathcal{E}| \ll x/P + x \exp\! ( - {\log x}/{\log P})$ , and the optimal choice is to take $P = \exp\! (\sqrt{\log x})$ .

We now have the tools to prove Proposition 3·2.

Proof of Proposition 3·2. We split the integers $n\leq x$ according to whether or not $P^+(n)^2 \mid n$ , so that

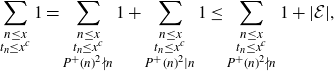\begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}} 1 &= \sum_{\substack{n\leq x \\ t_n \leq x^c \\ P^+(n)^2 \nmid n}} 1 + \sum_{\substack{n\leq x \\ t_n \leq x^c \\ P^+(n)^2 \mid n}} 1 \leq \sum_{\substack{n\leq x \\ t_n \leq x^c \\ P^+(n)^2 \nmid n}} 1 + |\mathcal{E}|,\end{align*}

where $\mathcal{E}$ is the set in Lemma 3·5. If $P^+(n)^2 \nmid n$ then we have $P^+(n) \leq t_n$ by Lemma 3·4, so

\begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c \\ P^+(n)^2 \nmid n}} 1 = \sum_{\substack{n\leq x \\ t_n \leq x^c \\ P^+(n)\leq x^c \\ P^+(n)^2 \nmid n}} 1\leq \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}} 1,\end{align*}

by positivity. Therefore

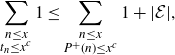\begin{align*}\sum_{\substack{n\leq x \\ t_n \leq x^c}} 1 \leq \sum_{\substack{n\leq x \\ P^+(n) \leq x^c}} 1 + |\mathcal{E}|,\end{align*}

and we finish with an appeal to Lemma 3·5.

The proof of Proposition 3·3 is slightly more circuitous, and relies upon an analysis of the number of subsets S of an interval with $\prod_{n \in S} n = \square$ . For this we require two more lemmas, though the reader may wish to skip ahead and see how the lemmas are used in establishing Proposition 3·3 before examining their proofs.

Lemma 3·6 (Subset squares and $t_n$ in intervals). Let $I = (x,x+y]$ be an interval. The number of subsets S of $I \cap \mathbb{N}$ such that $\prod_{n \in S} n = \square$ is equal to $2^r$ , where

\begin{align*}r &\;:\!=\; \#\{n > x \;:\; n+t_n \leq x+y\} = \#\{n \in I \;:\; n+t_n \in I\}.\end{align*}

Proof. The result is trivially true if $r=0$ , so assume $r\geq 1$ . Let $n_1 < \cdots < n_r$ be those integers with $x< n \leq n+t_n \leq x+y$ , and let $P_i$ be a non-empty product of integers in $[n_i,n_i+t_{n_i}]$ , including the endpoints, for which the product equals a square. Given $\ell_1 < \cdots < \ell_j \in (x,x+y]$ , define $v(\ell_1^{e_1}\cdots \ell_j^{e_j}) = \prod_{i : e_i \text{ odd}} \ell_i$ .

We claim that the $v(\prod_{i \in I} P_i), I \subset \{1,\ldots,r\}$ are distinct. If two are equal, select them minimally so that the $P_i$ are distinct and therefore $v(P_{i_1}\cdots P_{i_\ell}) = v(P_{j_1}\cdots P_{j_k})$ , say, with all the $i_*,j_*$ distinct. We may assume $i_1 < j_1$ , and therefore $n_1$ is part of the first product but not the second, a contradiction.

We claim that if $m_1 < \cdots < m_k \in (x,x+y]$ with $m_1\cdots m_k = \square$ then

\begin{align*}m_1\cdots m_k = v\Big(\prod_{i \in I}P_i \Big) \text{ for some } I \subset \{1,\ldots,r\}.\end{align*}

If not, select such a product with $m_1$ maximal. By definition $x<m_1\leq m_1+t_{m_1}\leq m_k \leq x+y$ , and so $m_1 = n_\ell$ for some $\ell$ . Then $\square = v(P_\ell m_1\cdots m_k) = v(n_\ell P_\ell m_2 \cdots m_k) = M_1\cdots M_k$ , where $M_1 > m_1$ . By the maximality of $m_1$ we have $M_1 \cdots M_k = v(\prod_{i\in I}P_i)$ for some $I \subset \{1,\ldots,r\}$ , and so

\begin{align*}m_1 \cdots m_k = v(P_\ell^2m_1\cdots m_k) = v(P_\ell M_1\cdots M_k) = v(P_\ell \cdot \prod_{i \in I} P_i),\end{align*}

a contradiction.

We deduce there are $2^r$ products of distinct integers in $(x,x+y]$ which give a square.

Lemma 3·7 ( $t_n$ in intervals and smooth numbers). Let $I = (x,x+y]$ be an interval. We have

\begin{align*}\#\{n > x \;:\; n+t_n \leq x+y\} \geq \#\{y-\text{smooth integers in } I\} - \pi(y).\end{align*}

Proof. Let

$$N \;:\!=\; S_\square(x+y,y)\backslash S_\square(x,y) = \{n_1,\ldots,n_m\}$$

and let $\{n_1,\ldots,n_k\}$ be the largest subset of N such that if $\prod_{i \in I} n_i$ is a square with $I \subset \{1,\ldots,k\}$ then $I = \varnothing$ (that is, they are the largest multiplicatively independent subset in $\mathbb{Z}$ modulo squares), so $k\leq \pi(y)$ .

Any subproduct of $n_{k+1}\cdots n_m$ is therefore dependent on $n_1,\ldots,n_k$ . That is, if $J \subset \{k+1,\ldots,m\}$ then there exists $J = J(I) \subset \{1,\ldots,k\}$ such that

\begin{align*}\prod_{j \in J} n_j \cdot \prod_{i \in I(J)}n_i = \square.\end{align*}

These products are distinct since the sets J are distinct. The number of square products is therefore $\geq 2^{m-k}$ . Combining this with Lemma 3·6 yields

\begin{align*}\#\{n \;:\; x < n \leq n+t_n \leq x+y\}\geq m-k &\geq \Psi_\square(x+y,y) - \Psi(x,y) - \pi(y).\end{align*}

Proof of Proposition 3·3. If x is sufficiently large and $P^+(n) > x^{0.51}$ then [8, Corollary 1] implies $P^+(n)=t_n$ , and therefore

\begin{align*}\sum_{\substack{n\leq x \\ P^+(n) \leq x^c}} 1 = \sum_{\substack{n\leq x \\ P^+(n) \leq x^{0.51}}} 1 + \sum_{\substack{n\leq x \\ x^{0.51}<t_n \leq x^c}} 1.\end{align*}

The proposition in the case $c>0.51$ therefore follows from the proposition in the case $c\leq 0.51$ , so we may assume $c\leq 0.51$ .

Let $I = (x,x+y]$ so Lemma 3·7 reads as

\begin{align*}\#\{n \;:\; x< n \leq n+t_n \leq x+y\}\geq \#\{n\in I \;:\; P^*(n)\leq y\} - \pi(y).\end{align*}

Now, since $P^*(n)\leq t_n$ we have

\begin{align*}\#\{n \;:\; x< n \leq n+t_n \leq x+y\} &\leq \#\{n \in I \;:\; t_n \leq y\} \\ &=\#\{n\in I \;:\; P^*(n)\leq y\} - \#\{n\in I \;:\; P^*(n)\leq y < t_n\}.\end{align*}

Combining the last two equations gives $\#\{n\in I \;:\; P^*(n)\leq y < t_n\} \leq \pi(y)$ , and so

\begin{align*}\#\{n \in I \;:\; P^*(n)\leq y\} &\leq \#\{n \in I\;:\; t_n \leq y\} + \#\{n\in I \;:\; P^*(n)\leq y < t_n\} \\ &\leq \#\{n \in I\;:\; t_n \leq y\} + \pi(y).\end{align*}

Summing this up over intervals of length y gives

\begin{align*}\Psi_\square(x,y) &\leq \#\{n \in I\;:\; t_n \leq y\} + O(x/\log y).\end{align*}

Proof of Theorem 1·1. By [8, Corollary 1] we may assume $c\leq 0.51$ . We have

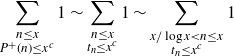\begin{align*}\sum_{\substack{n\leq x \\ P^+(n) \leq x^c}} 1 \sim \sum_{\substack{n\leq x \\ t_n \leq x^c}} 1 \sim \sum_{\substack{x/\log x < n\leq x \\ t_n \leq x^c}} 1\end{align*}

by Theorem 3·1 and trivial estimation. We split the sum acording to the size of $t_n$ so that

\begin{align*}\sum_{\substack{x/\log x < n\leq x \\ t_n \leq x^c}} 1 &\sim \sum_{\substack{n\leq x \\ t_n \leq n^c}} 1 + O \Big(\sum_{\substack{n\leq x \\ (x/\log x)^c < t_n \leq x^c}} 1 \Big).\end{align*}

We must show

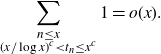\begin{align*}\sum_{\substack{n\leq x \\ (x/\log x)^c < t_n \leq x^c}} 1 = o(x).\end{align*}

We split the sum over n according to whether or not $n \in \mathcal{E}$ , with $\mathcal{E}$ as in Lemma 3·5. The size of $\mathcal{E}$ is o(x). If $n \not \in \mathcal{E}$ then $P^+(n) \leq t_n$ , and we may further split the sum with $n \not \in \mathcal{E}$ according to whether or not $P^+(n) \leq (x/\log x)^c$ . Hence

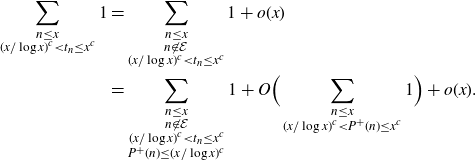\begin{align*}\sum_{\substack{n\leq x \\ (x/\log x)^c < t_n \leq x^c}} 1 &= \sum_{\substack{n\leq x \\ n \not \in \mathcal{E} \\ (x/\log x)^c < t_n \leq x^c}} 1+o(x)\\&= \sum_{\substack{n\leq x \\ n \not \in \mathcal{E} \\ (x/\log x)^c < t_n \leq x^c \\ P^+(n) \leq (x/\log x)^c}} 1 + O \Big(\sum_{\substack{n\leq x \\ (x/\log x)^c < P^+(n) \leq x^c}} 1 \Big)+o(x).\end{align*}

The O-term has size $\ll x({\log \log x}/{\log x})$ . For the other sum, we set $Y = (x/\log x)^c$ and note that

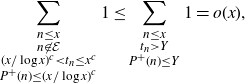\begin{align*}\sum_{\substack{n\leq x \\ n \not \in \mathcal{E} \\ (x/\log x)^c < t_n \leq x^c \\ P^+(n) \leq (x/\log x)^c}} 1 &\leq \sum_{\substack{n\leq x \\ t_n > Y \\ P^+(n) \leq Y}} 1 = o(x),\end{align*}

by the argument in the proof of Proposition 3·3.

Since we similarly have

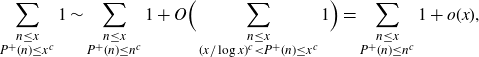\begin{align*}\sum_{\substack{n\leq x \\ P^+(n) \leq x^c}} 1 \sim \sum_{\substack{n\leq x \\ P^+(n) \leq n^c}} 1 + O\Big(\sum_{\substack{n\leq x \\ (x/\log x)^c < P^+(n) \leq x^c}} 1 \Big) = \sum_{\substack{n\leq x \\ P^+(n) \leq n^c}} 1 + o(x),\end{align*}

this completes the proof.

4. Small values of $t_n$ : Proof of Theorem 1·2

The proof of Theorem 1·2 uses estimates for smooth numbers and some elementary combinatorics. We introduce parameters $y < L \leq x^{o(1)}$ , and the first idea is to find many short intervals $I \subset [1,x]$ of length L which contain roughly the expected number of y–smooth numbers.

Lemma 4·1 (Many intervals with expected number of smooths). Let x be sufficiently large, and let $y < L \leq x^{o(1)}$ with $y \geq \exp\! ((\!\log x)^{1/100})$ . Then there are $\gg \Psi(x,y)L^{-1}$ disjoint intervals $I \subset [x/\log x,x]$ of length L such that

Proof. With y as in the statement of the lemma we have by [10, Theorem 1] that the number of smooth numbers in $(x/\log x,x]$ is $\geq (1-o(1)) \Psi(x,y)$ .

For k a positive integer write $I = I_k = (kL,(k+1)L]$ , and let $\mathcal{I}$ denote those I which are contained in $(x/\log x,x]$ . By trivial estimation $\# \mathcal{I} \asymp x/L$ . Let $\delta > 0$ be a sufficiently small positive constant, and write $\mathcal{I} = \mathcal{G}\cup \mathcal{G}^c$ , where $I \in \mathcal{G}$ if $\# \{y-\text{smooth integers in } I\} > \delta L \Psi(x,y)/x$ . If $\delta$ is sufficiently small the number of y-smooth integers in all of $\mathcal{G}^c$ is $O(\delta \Psi(x,y))$ . Since $\# \{y-\text{smooth integers in } I\} \leq L$ we find that $\#\mathcal{G} \gg {\Psi(x,y)}/{L}$ .

If a short interval contains sufficiently many y–smooth numbers, then we can construct an integer n with small $t_n$ .

Lemma 4·2 (Build small $t_n$ with many smooths). Let I be an interval of length L such that

\begin{align*}\#\{y-\text{smooth integers in } I\} > \pi(y).\end{align*}

Then there exists an integer $n \in I$ with $t_n \leq L$ .

Proof. Let $p_1 < \cdots < p_R$ be the primes $\leq y$ , so that $\pi(y) = R$ . A y–smooth integer n may be written as $n = \prod_{i=1}^R p_i^{e_i}$ , where $e_i$ is a nonnegative integer. By considering only the parity of $e_i$ we obtain a map $\theta\;:\; \{y-\text{smooth integers}\} \rightarrow \mathbb{F}_2^{R}$ given by

(1) \begin{align}\theta(n) = (e_1\ (\text{mod}\ 2),\ldots, e_R\ (\text{mod}\ 2)).\end{align}

Let $m_1,\ldots,m_M$ be the y–smooth integers in I. By assumption, we have $M > R$ . Given $J \subset \{1,\ldots,M\}$ , let $n_J = \prod_{j \in J} m_j$ . The number $2^M$ of subsets of $\{1,\ldots,M\}$ is greater than $2^R = \#\mathbb{F}_2^R$ , so by the pigeonhole principle there exist distinct subsets J, J ^′ of $\{1,\ldots,M\}$ such that $\theta(n_J) = \theta(n_{J'})$ . By the definition of $\theta$ this implies

\begin{align*}\prod_{m \in J}m \cdot \prod_{m \in J'} m = \square.\end{align*}

Since $J \neq J'$ we see that $J \Delta J' \neq \varnothing$ and $\prod_{m \in J \Delta J'} m = \square$ . The least element n of $J \Delta J'$ is then the desired integer.

Proof of Theorem 1·2. We define $y = \exp\!(\frac{\sqrt{2}}{2} \sqrt{\log x \log \log x})$ and

\begin{align*}L = \exp\! \left( \left(\sqrt{2} + (\!\log \log x)^{-1/2} \right)\sqrt{\log x \log \log x}\right).\end{align*}

By [10, Theorem 1] and Lemma 4·1 there are $\gg x L^{-1} \rho \big( {\log x}/{\log y}\big)$ intervals $I \subset [x/\log x,x]$ of length L such that each interval I contains $\gg L \rho \Big( {\log x}/{\log y}\Big)$ numbers which are y–smooth. By [11, Corollary 2·3], the number of y–smooth integers in each interval I of length L is therefore

\begin{align*}&\gg y \exp\! \left((\!\log x)^{1/2} (\!\log \log x)^{1/4} \right),\end{align*}

hence the number of y–smooth integers in each interval is $> \pi(y) \sim {y}/{\log y}$ . We conclude by applying Lemma 4·2.

We remark that our proof of Theorem 1·2 has some similarities to heuristic run-time analysis of factoring algorithms [13, p. 1477] (see also [2] and [8, section 1]).

5. Large integral points on hyperelliptic curves: Proof of Theorem 1·3

As mentioned in the introduction, the proof of Theorem 1·3 draws on ingredients in the proof of Theorem 1·2. We also need an additional lemma, which provides for the existence of sets with large symmetric difference provided we have sufficiently many sets upon which to draw.

Lemma 5·1 (Many subsets implies a large symmetric difference). Let N be large and let $S_1,\ldots,S_K$ be distinct subsets of $\{1,\ldots,N\}$ . If $K \geq 2^Q$ with $Q \geq N^{1/100}$ , then there exist $i\neq j$ such that

\begin{align*}|S_i \Delta S_j |> \frac{1}{6} \frac{Q}{\log N}.\end{align*}

Proof. Let A be an arbitrarily chosen (nonempty) subset $S_i$ . For any other subset S, we may uniquely write S as the disjoint union $S = S' \cup S_A$ , where $S' \cap A = \varnothing$ and $S_A \subset A$ . Observe that $A \Delta S = (A \backslash S) \cup (S \backslash A) = (A \backslash S_A) \cup S'$ . Let $\delta \geq {1}/{100}$ be a parameter. If $|A \Delta S |\leq \delta{Q}/{\log N}$ , then $|S'| \leq \delta{Q}/{\log N}$ and $|A \backslash S_A| \leq \delta{Q}/{\log N}$ .

The number of choices for the set S ^′ is

\begin{align*}\leq \sum_{0\leq k \leq \delta Q/\log N} \left(\substack{N\\[2pt] k}\right),\end{align*}

and this is also a bound on the number of choices for the set $S_A$ . By the upper bound $\left(\substack{N\\[2pt] k}\right) \leq (eN/k)^k$ , valid for $k\geq 1$ , we find

\begin{align*}\sum_{0\leq k \leq \delta Q/\log N} \left(\substack{N\\[2pt] k}\right) \leq 1 + (eN)^{\delta Q/\log N} \sum_{k\geq 1}k^{-k} \leq (3N)^{\delta Q/\log N}\leq \exp\! \left(2\delta Q \right).\end{align*}

It follows that the total number of choices of subset S such that $|A \Delta S| \leq \delta Q /\log N$ is $\leq \exp\!(4\delta Q) < 1.95^Q$ , the last inequality following if we choose $\delta = {1}/{6}$ , say. Since there are $K \geq 2^Q$ subsets, there must be some subset $S_i$ such that $|A \Delta S_i| > {Q}/(6\log N)$ .

Proof of Theorem 1·3. Let x be a large integer. As in the proof of Theorem 1·2, we set our smoothness parameter $y = \exp\! \Big(({\sqrt{2}}/{2}) \sqrt{\log x \log \log x} \Big)$ . Given a constant $C > \sqrt{2}$ , we also define a length parameter $L = y^{C\sqrt{2}}$ .

We may apply Lemma 4·1 to deduce the existence of many disjoint intervals $I \subset [x/\log x, x]$ of length L such that the number of y–smooth integers in I is $\gg L \Psi(x,y)/x$ . We fix one such interval I, and note that by the argument of Theorem 1·3 the number of y–smooth integers in I is $\geq \exp\! \big((C - {\sqrt{2}}/{2} - o(1) )\sqrt{\log x \log \log x} \big)$ . If we let M denote the number of y–smooth integers in I, and $R = \pi(y)$ , then we see that

\begin{align*}M - R &\geq \exp\! \bigg(\Big(C - \frac{\sqrt{2}}{2} - o(1) \Big)\sqrt{\log x \log \log x} \bigg)\geq L^{1 - \frac{\sqrt{2}}{2C} - o(1)}.\end{align*}

Let $n_1,\ldots,n_M$ be the y–smooth integers in I. Given a subset $S\subset\{1,\ldots,M\}$ we may construct the y–smooth integer $n_S = \prod_{s \in S} n_s$ , and then map $n_S$ to $\mathbb{F}_2^R$ using the map $\theta$ from (1). By the pigeonhole principle, there is some $v \in \mathbb{F}_2^R$ and $\geq 2^{M-R}$ subsets S of $\{1,\ldots,M\}$ such that $\theta(n_S)=v$ for every such S. We apply Lemma 5·1 to obtain the existence of two subsets, call them S and T, of $\{1,\ldots,M\}$ such that

\begin{align*}|S \Delta T| &\geq \frac{1}{6} \frac{M-R}{\log M}\geq L^{1 - \frac{\sqrt{2}}{2C} - o(1)}.\end{align*}

By construction we have $\prod_{s \in S \Delta T} n_s = \square$ . We may arrange the integers $n_s$ in increasing order and write them as $n,n+j_1,\ldots,n+j_V$ for some integer $n\in [x/\log x,x]$ and some integers $1\leq j_1 < j_2 < \cdots < j_V \leq L$ . It follows that $n(n+j_V)\prod_{i=1}^{V-1} (n+j_i)$ is a square.

We claim that setting $J = j_V$ gives rise to a J as in the statement of the theorem. First, note that $V-1\geq L^{1 - \frac{\sqrt{2}}{2C} - o(1)}-2 \geq J^{1-c}$ , the last inequality holding if we set $C = {\sqrt{2}}/{c}$ , say. Since $x\leq n(\!\log n)^2$ we see that $L \leq \exp\! \left((C+o(1))\sqrt{\log n \log \log n} \right)$ , which implies $\log n \geq \left(({1-o(1)})/({2C^2})\right)({(\!\log L)^2}/{\log \log L})$ . Recalling our choice for C and that $J\leq L$ we find

\begin{align*}n&\geq \exp\! \left(\frac{c^2}{5}\frac{(\!\log J)^2}{\log \log J} \right).\end{align*}

Since every large x gives rise to such a J, and since $J \geq L^{1/3}$ , say, which tends to infinity with x, we may take J to be arbitrarily large, as claimed.

We close this section with some comments on Theorem 1·3. In particular, it is worth comparing Theorem 1·3 with more trivial considerations.

First, we note that it is easy to obtain points (x, y) on a hyperelliptic curve of large genus if we allow $x=0$ (so that y is large). Indeed, consider the hyperelliptic curve $y^2 = P(x)= x^g + D^2$ , where $g\geq 5$ is large and D is a large positive integer. The point (0,D) clearly lies on the hyperelliptic curve and, since the height H of P is $D^2$ , we see the integral point (0,D) has height $\gg H^{1/2}$ . We might expect that all integral points on a hyperelliptic curve $y^2= P(x)$ have height $\ll H^{O(1)}$ , so this trivial construction is already fairly sharp.

Second, we consider hyperelliptic curves with integral points (x, y) where $x\neq 0$ . The hyperelliptic curve $y^2 =P(x)= \prod_{i=1}^J (x+j), J \geq 5$ , is similar to the curves constructed in Theorem 1·3, and this curve has the integral point $(\!-\!J,0)$ . The polynomial P has height $H=J!$ , so the point $(\!-\!J,0)$ on the curve has height $\gg \log H/\log \log H$ for large J. In contrast, Theorem 1·3 provides integral points (x, y) on curves $y^2 = P(x)$ with $xy\neq 0$ and

\begin{align*}x\gtrapprox (\!\log H)^{\frac{\log \log H}{\log \log \log H}} \gg_A (\!\log H)^A,\end{align*}

where H is the height of P.

It would be very interesting to construct hyperelliptic curves of large genus having integral points (x, y) with $x\geq H^c$ , for $c>0$ some fixed constant.

6. Lower bounds on $t_n$ : Proof of Theorem 1·4

If n is a large non-square integer, then by definition $n(n+t_n)\prod_{i=1}^s (n+j_i) = \square$ , where $1\leq j_1 < \cdots < j_s < t_n$ are integers (obviously we must have $s < t_n$ ). If $t_n$ is very small compared to n, then the curve

(2) \begin{align}y^2 = x(x+J)\prod_{i=1}^s(x+j_i)\end{align}

contains an integral point with x extremely large (here and throughout the section we write $J = t_n$ in keeping with the notation of our other theorems). We rely on a uniform bound for the height of integral points on hyperelliptic curves due to Bérczes, Evertse and Győry [1]. Their method utilises linear forms in logarithms.

We use different arguments depending on the size of s, with s as in (2). When $s=0$ trivial arguments suffice to bound the size of x. If $s\geq 1$ but is smaller than a small power of J, then we consider the hyperelliptic equation (2) directly and apply the result of Bérczes, Evertse and Győry. When s is larger than a small power of J it is more efficient to extract a suitable system of generalised Pell equations from (2) and bound the size of solutions to these Pell equations. The coefficients of the Pell equations have size controlled by prime divisors $\leq J$ , and we can use some elementary arguments to find a system with coefficients that are smaller than what a trivial bound would give. The final bound results from balancing the arguments coming from small s and large s.

Lemma 6·1 (Trivial case, $s=0$ ). Let $J\geq 1$ be an integer. If x and y are positive integers with $y^2 = x(x+J)$ , then $x\leq J^2$ .

Proof. If x and $x+J$ have greatest common divisor $d\geq 1$ , then $d \mid J$ . We change variables $x = dz$ and find $(y/d)^2 = z(z+J/d)$ , where $(z,z+J/d)=1$ . Then $z=a^2$ and $z+J/d = b^2$ for some positive integers $b>a$ . Then

\begin{align*}J/d = b^2-a^2 = (b+a)(b-a) \geq b+a,\end{align*}

so $a,b\leq J/d$ . Then $z=a^2\leq J^2/d^2$ and $x=dz \leq J^2/d\leq J^2$ .

The next lemma is the theorem of Bérczes, Evertse and Győry [1] in the special case we require.

Lemma 6·2 (Height of integral points). Let $P(x) = \sum_{i=0}^n a_i x^i \in \mathbb{Z}[x]$ with $\deg(P)\geq 3$ and no repeated roots. Write $\max_i |a_i| =H$ . If x and y are positive integers with $y^2 = P(x)$ then

\begin{align*}\max(\!\log x, \log y) &\leq (4n)^{212n^4}H^{50n^4}.\end{align*}

Proof. This is [1, Theorem 2·2] with $K = \mathbb{Q}$ and S equal to the infinite place of $\mathbb{Q}$ , where $b=1$ in [1, (2·5)].

The following lemma is useful when s is small.

Lemma 6·3 (Bound on height when is small). Let $J\geq 2$ be an integer, and let $1\leq j_1 < \cdots < j_s < J$ be integers, where $s\geq 1$ . If x and y are positive integers with $y^2 = x(x+J)\prod_{i=1}^s (x+j_i)$ then $\log x \leq \exp\! \big(O(s^5 \log J) \big)$ .

Proof. The integer polynomial $x(x+J)\prod_{i=1}^s (x+j_i)$ has degree $s+2$ and clearly has no repeated roots. The coefficients of the polynomial all have size $\leq J^{s+1}$ , so by Lemma 6·2 we see any solution to $y^2 = x(x+J)\prod_{i=1}^s (x+j_i)$ satisfies

\begin{align*}\log x &\leq\big (4(s+2)\big)^{212(s+2)^4} (J^{s+1})^{50(s+2)^4}\leq \exp\! \big(O(s^5 \log J) \big).\end{align*}

When s is large we argue more carefully. We use the following lemma to control the coefficients of an auxiliary hyperelliptic equation.

Lemma 6·4 (Finding numbers with fewer prime factors). Let J be a sufficiently large positive integer, and let $b_1,\ldots,b_t$ be positive integers all of whose prime factors are $\leq J$ . If $100\leq t \leq J^{1/2}/\log J$ and for all $i\neq j$ , then there exist distinct $b_i,b_j,b_k$ with

\begin{align*}\omega(b_i),\omega(b_j),\omega(b_k) \ll \frac{J}{t\log J}.\end{align*}

Proof. We observe that, by the prime number theorem, any distinct $b_i$ and $b_j$ have $\ll \log J/\log \log J\leq \log J$ prime factors in common, since $\text{gcd}(b_i,b_j)\leq J$ . Let $s_i$ denote the set of prime factors of $b_i$ . Note that $|s_i \cap s_j| \leq \log J$ for any $i\neq j$ , and that each $s_i$ is contained in the set of all primes $\leq J$ .

Without loss of generality we may assume $|s_1| \geq |s_2| \geq \cdots \geq |s_t|$ . We claim that

(3) \begin{align}|s_1 \cup \cdots \cup s_r| \geq r|s_r| - \frac{r(r-1)}{2}\log J\end{align}

for each $1\leq r \leq t$ . This inequality trivially holds for $r=1$ , which provides the base case for an inductive argument. Let $A = s_1 \cup \cdots \cup s_r$ , so that by inclusion-exclusion and the induction hypothesis

\begin{align*}|s_1 \cup \cdots \cup s_{r+1}| &\geq r|s_r| - \frac{r(r-1)}{2}\log J + |s_{r+1}| - \sum_{i=1}^r |s_i \cap s_{r+1}|.\end{align*}

Since $|s_i \cap s_{r+1}| \leq \log J$ and $|s_r| \geq |s_{r+1}|$ , we obtain $|A \cap s_{r+1}| \geq (r+1)|s_{r+1}| - ({r(r+1)}/{2})\log J$ , as desired. This completes the proof of the claim.

Applying (3) yields $|s_r| \leq ({1}/{r})|s_1 \cup \cdots \cup s_r| + ({r-1})\log J/{2}$ for any $1\leq r \leq t$ . Since each set $s_i$ is contained in the set of all primes $\leq J$ we have $|s_r| \ll {J}/{r\log J} + r\log J$ , and since $r\leq t\leq J^{1/2}/\log J$ we have $|s_r| \ll {J}/{r\log J}$ . We finish the proof by taking $i=t-2,j=t-1$ , and $k=t$ .

We are now ready to obtain a bound when s is large.

Lemma 6·5 (Bound on height when is large). Let J be a sufficiently large positive integer, and let $1\leq j_1 < \cdots < j_s < J$ be integers, where $J^{1/100}\leq s < J$ . If x and y are positive integers with $y^2 = x(x+J)\prod_{i=1}^s (x+j_i)$ then

\begin{align*}\log x &\leq \exp\! \bigg(O \Big(\frac{J}{t\log J} \Big) \bigg),\end{align*}

where t is any integer satisfying $J^{1/100} \leq t \leq \min (s, J^{1/2}/\log J)$ .

Proof. We write $j_0 = 0$ and $j_{s+1} = J$ , so that the hyperelliptic equation is $y^2 = \prod_{i=0}^{s+2} (x+j_i)$ . If $d \mid( x+j_i)$ and $d\mid (x+j_{i'})$ then $d\mid |j_i - j_{i'}| \leq J$ , so the greatest common divisor of any two distinct $x+j_i$ is $\leq J$ . We may therefore uniquely write $x+j_i = b_i z_i^2$ , where $b_i$ is squarefree and divisible only by primes $\leq J$ . Observe that $\text{gcd}(b_i,b_{i'}) \leq J$ for $i\neq i'$ .

Choose any t of the $b_i$ , with t as in statement of the lemma. By Lemma 6·4 there exist three distinct $b_i,b_k$ , and $b_\ell$ with $\omega(b_i),\omega(b_k),\omega(b_\ell) \ll {J}/{t\log J}$ . From the equations

\begin{align*}x+j_i &= b_i z_i^2, \ \ \ \ \ x+j_k = b_k z_k^2, \ \ \ \ \ x+j_\ell = b_\ell z_\ell^2,\end{align*}

we deduce

(4) \begin{align}(b_kb_\ell z_kz_\ell)^2 &= b_kb_\ell(x+j_k)(x+j_\ell) = b_kb_\ell(b_iz_i^2+j_k-j_i)(b_iz_i^2+j_\ell-j_i).\end{align}

The quartic polynomial $b_kb_\ell(b_iz_i^2+j_k-j_i)(b_iz_i^2+j_\ell-j_i)$ has no repeated roots (since $j_k \neq j_\ell$ ) and has coefficients with absolute value

\begin{align*}\leq J^2 b_ib_kb_\ell \leq J^{2+\omega(b_i)+\omega(b_k)+\omega(b_\ell)}\leq \exp\!\big( O \left( J/t\right) \big).\end{align*}

We apply Lemma 6·2 to the hyperelliptic equation (4) to find

\begin{align*}\log z_i \leq 16^{212\cdot 4^4} \exp\!\big( O \left( J/t\right) \big)^{50\cdot 4^4}\ll \exp\!\big( O \left( J/t\right) \big).\end{align*}

Since $x+j_i = b_i z_i^2$ this implies $\log x \leq \exp\!\left( O \left( J/t\right) \right)$ .

Proof of Theorem 1·4. Let n be a large non-square integer. Write $J = t_n$ so that by definition we have $y^2 = n(n+J) \prod_{i=1}^s (n+j_i)$ for some integers $1\leq j_i < \cdots < j_s< J$ and $s\geq 0$ . If $s=0$ then Lemma 6·1 implies $n\leq J^2$ . We may therefore assume $s\geq 1$ .

If J is bounded then by Lemma 6·2 we see n is effectively bounded in terms of J, so we may assume J is sufficiently large. We define $t = \lfloor (J/\log J)^{1/6}\rfloor$ . If $1\leq s\leq t$ then Lemma 6·3 gives

\begin{align*}\log n &\leq \exp\! \big(O(t^5\log J)\big) = \exp\! \Big(O\big(J^{5/6}(\!\log J)^{1/6} \big) \Big).\end{align*}

If $t\leq s < J$ then applying Lemma 6·5 gives

\begin{align*}\log n &\leq \exp\! \big(O(J/t)\big) = \exp\! \Big(O\big(J^{5/6}(\!\log J)^{1/6} \big) \Big).\end{align*}

Therefore, in any case $\log n \leq \exp\! \Big(O\big(J^{5/6}(\!\log J)^{1/6} \big) \Big)$ , which implies $\log \log n \ll J^{5/6} (\!\log J)^{1/6}$ . This last inequality implies in turn that $J \gg (\!\log \log n)^{6/5}(\!\log \log \log n)^{-1/5}$ .

One can likely obtain improvements to Theorem 1·4 by working with a version of Lemma 6·2 which exploits particular features of the hyperelliptic equation (2).

We expect that one can obtain a stronger result than Theorem 1·4.

Conjecture 1. Let $c \in (0,1)$ be a fixed constant, and assume n is a non-square integer which is sufficiently large in terms of c. Then $t_n \geq (\!\log n)^{1-c}$ .