Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T18:00:42.143Z Has data issue: false hasContentIssue false
  • English
  • Français

Primitive prime divisors in the critical orbits of one-parameter families of rational polynomials

Part of: Sequences and sets Elementary number theory Complex dynamical systems

Published online by Cambridge University Press:  25 January 2021

RUFEI REN
RUFEI REN*
Affiliation:
Department of Mathematics, Fudan University, 220 Handan Rd., Yangpu District, Shanghai200433, China. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a polynomial 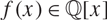$f(x)\in\mathbb{Q}[x]$ and rational numbers c, u, we put 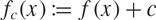$f_c(x)\coloneqq f(x)+c$, and consider the Zsigmondy set 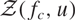$\calZ(f_c,u)$ associated to the sequence 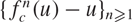$\{f_c^n(u)-u\}_{n\geq 1}$, see Definition 1.1, where 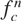$f_c^n$ is the n-st iteration of fc. In this paper, we prove that if u is a rational critical point of f, then there exists an Mf > 0 such that 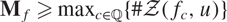$\mathbf M_f\geq \max_{c\in \mathbb{Q}}\{\#\calZ(f_c,u)\}$.

MSC classification

Primary: 11B37: Recurrences
Secondary: 37F10: Polynomials; rational maps; entire and meromorphic functions 11A41: Primes
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 171 , Issue 3 , November 2021 , pp. 569 - 584
Copyright
© Cambridge Philosophical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bang, A. S.. Talteoretiske undersøgelser. Tidsskrift Mat. (5) 4 (1886), 70–80; 130–137.Google Scholar
Carmichael, R. D.. On the numerical factors of the arithmetic forms αn ± βn. Ann. of Math. (1/4) 15 (1913), 49–70.CrossRefGoogle Scholar
Doerksen, K. and Haensch, A.. Primitive prime divisors in zero orbits of polynomials. Integers (3) 12 (2011), 465–473.Google Scholar
Gratton, C., Nguyen, K. and Tucker, T. J.. ABC implies primitive prime divisors in arithmetic dynamic. Bull. Lond. Math. Soc. (6) 45 (2013), 1194–1208.CrossRefGoogle Scholar
Ingram, P. and Silverman, J.. Primitive divisors in arithmetic dynamics. Math. Proc. Camb. Phil. Soc. (2) 146 (2009), 289–302.CrossRefGoogle Scholar
Krieger, H.. Primitive prime divisors in the critical orbit of zd + c. Int. Math. Res. Not. IMRN 23 (2013), 5498–5525.CrossRefGoogle Scholar
Rice, B.. Primitive prime divisors in polynomial arithmetic dynamics. Integers (1) 7 (2007), A26, 1–16.Google Scholar
Schinzel, A.. Primitive divisors of the expression an − bn in algebraic number fields. J. Reine Angew. Math. 268/269 (1974), 27–33.Google Scholar
Zsigmondy, K.. Zur Theorie der Potenzreste. Monatsh. Math. Phys. (1) 3 (1892), 265–284.CrossRefGoogle Scholar
Evertse, J. H.. The number of algebraic numbers of given degree approximating a given algebraic number. Analytic Number Theory, Motohashi, Y. (ed.), London Math. Soc. Lecture Notes Ser. 247, (Cambridge University Press 1998), 53–83.Google Scholar