Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T01:33:55.933Z Has data issue: false hasContentIssue false
  • English
  • Français

Popular differences for corners in Abelian groups

Part of: Sequences and sets

Published online by Cambridge University Press:  07 October 2020

AARON BERGER
AARON BERGER*
Affiliation:
Department of Mathematics, MIT, 182 Memorial Drive, Cambridge, MA02142, U.S.A., e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a compact abelian group G, a corner in G × G is a triple of points (x, y), (x, y+d), (x+d, y). The classical corners theorem of Ajtai and Szemerédi implies that for every α > 0, there is some δ > 0 such that every subset A ⊂ G × G of density α contains a δ fraction of all corners in G × G, as x, y, d range over G.

Recently, Mandache proved a “popular differences” version of this result in the finite field case 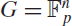$G = {\mathbb{F}}_p^n$, showing that for any subset A ⊂ G × G of density α, one can fix d ≠ 0 such that A contains a large fraction, now known to be approximately α4, of all corners with difference d, as x, y vary over G. We generalise Mandache’s result to all compact abelian groups G, as well as the case of corners in 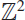$\mathbb{Z}^2$.

MSC classification

Primary: 11B30: Arithmetic combinatorics; higher degree uniformity
Secondary: 11B25: Arithmetic progressions
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 171 , Issue 1 , July 2021 , pp. 207 - 225
Copyright
© Cambridge Philosophical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ajtai, M. and Szemerédi, E.. Sets of lattice points that form no squares. Stud. Sci. Math. Hungar 9, 1975 (1974), 9–11.Google Scholar
Bergelson, V., Host, B. and Kra, B.. Multiple recurrence and nilsequences. Invent. Math. 160, 2 (2005), 261–303. With an appendix by Imre Rusza.CrossRefGoogle Scholar
Bourgain, J.. On triples in arithmetic progression. Geom. Funct. Anal. 9 (1999), 968–984.CrossRefGoogle Scholar
Fox, J., Sah, A., Sawhney, M., Stoner, D. and Zhao, Y.. Triforce and corners. Math. Proc. Cambridge Philos. Soc., 1–15.Google Scholar
Green, B.. A Szemerédi-type regularity lemma in abelian groups, with applications. Geom. Funct. Anal. 15, 2 (2005), 340–376.CrossRefGoogle Scholar
Green, B. and Tao, T.. An arithmetic regularity lemma, an associated counting lemma, and applications. In An Irregular Mind (Szemerédi is 70) ed. Bárány, I., Solymosi, J., Sági, G.. (Springer, 2010), pp. 261–334.CrossRefGoogle Scholar
Lovász, L. and Szegedy, B.. Limits of dense graph sequences. J. Combin. Theory Ser. B 96, 6 (2006), 933–957.CrossRefGoogle Scholar
Lovász, L. and Szegedy, B.. Szemerédi’s lemma for the analyst. Geom. Funct. Anal. 17, 1 (2007), 252–270.CrossRefGoogle Scholar
Mandache, M.. A variant of the corners theorem. arXiv preprint arXiv:1804.03972 (2018).Google Scholar
Tao, T.. A proof of Roth’s theorem. https://terrytao.wordpress.com/2014/04/24/a-proof-of-roths-theorem/ (2014). Accessed: 2019-8-21.Google Scholar