Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-14T07:26:54.646Z Has data issue: false hasContentIssue false
  • English
  • Français

The polarization constant of finite dimensional complex spaces is one

Part of: Basic linear algebra Measures, integration, derivative, holomorphy General theory of linear operators Nonlinear functional analysis

Published online by Cambridge University Press:  04 March 2021

VERÓNICA DIMANT ,
DANIEL GALICER  and
JORGE TOMÁS RODRÍGUEZ
VERÓNICA DIMANT
Affiliation:
Departamento de Matemática y Ciencias, Universidad de San Andrés, Vito Dumas 284, (B 1644BID) Victoria, Buenos Aires, Argentina and CONICET. e-mail : [email protected]
DANIEL GALICER
Affiliation:
Departamento de Matemática, Facultad de Ciencias Exactas y Naturales, Universidad de Buenos Aires, Intendente Güiraldes 2160, (1428) Buenos Aires, Argentina and CONICET. e-mail : [email protected]
JORGE TOMÁS RODRÍGUEZ
Affiliation:
Departamento de Matemática and NUCOMPA, Facultad de Cs. Exactas, Universidad Nacional del Centro de la Provincia de Buenos Aires, Pinto 399, (7000) Tandil, Argentina and CONICET. e-mail : [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The polarization constant of a Banach space X is defined as

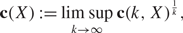\[{\text{c}}(X){\text{ }}{\text{ }}\mathop {\lim }\limits_{k \to \infty } {\text{ }}\sup {\text{c}}{(k,X)^{\frac{1}{k}}},\]

where 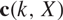\[{\text{c}}(k,X)\] stands for the best constant 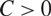\[C > 0\] such that 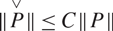\[\mathop P\limits^ \vee \leqslant CP\] for every k-homogeneous polynomial 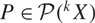\[P \in \mathcal{P}{(^k}X)\]. We show that if X is a finite dimensional complex space then 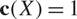\[{\text{c}}(X) = 1\]. We derive some consequences of this fact regarding the convergence of analytic functions on such spaces.

The result is no longer true in the real setting. Here we relate this constant with the so-called Bochnak’s complexification procedure.

We also study some other properties connected with polarization. Namely, we provide necessary conditions related to the geometry of X for 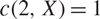\[c(2,X) = 1\] to hold. Additionally we link polarization constants with certain estimates of the nuclear norm of the product of polynomials.

MSC classification

Primary: 46G25: (Spaces of) multilinear mappings, polynomials 47A07: Forms (bilinear, sesquilinear, multilinear)
Secondary: 15A69: Multilinear algebra, tensor products 46T25: Holomorphic maps
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 172 , Issue 1 , January 2022 , pp. 105 - 123
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abuabara, T.. A version of the Paley–Wiener–Schwartz theorem in infinite dimensions. North-Holland Math. Stud., 34 (1979), 1–29.CrossRefGoogle Scholar
Anagnostopoulos, V. and Revesz, S. G., Polarisation constants for products of linear functionals over 2 and ℂ2 and Chebyshev constants of the unit sphere. Publ. Math. Debrecen. 68(1-2), (2006), 75–83.Google Scholar
Aron, R. M. and Berner, P. D.. A Hahn–Banach extension theorem for analytic mappings. Bull. Soc. Math. France., 106, (1978), 3–24.CrossRefGoogle Scholar
Banach, S.. Über homogene polynome in (L 2). Studia Math., 7(1), (1938), 36–44.CrossRefGoogle Scholar
Bayart, F.. Weak-closure and polarisation constant by Gaussian measure. Math. Z., 264(2), (2010), 459–468.CrossRefGoogle Scholar
Bentez, C. and Sarantopoulos, Y.. Characterisation of real inner product spaces by means of symmetrical bilinear forms. J. Math. Anal. Appl., 180(1), (1993), 207–220.CrossRefGoogle Scholar
Bentez, C., Sarantopoulos, Y., and Tonge, A.. Lower bounds for norms of products of polynomials. Math. Proc. Camb. Phil. Soc., 124(3), (1998), 395–408.CrossRefGoogle Scholar
Bergh, J. and Löfström, J.. Interpolation Spaces: an Introduction, vol. 223 (Springer-Verlag, 1976).CrossRefGoogle Scholar
Carando, D., Pinasco, D. and Rodrguez, J. T.. On the linear polarisation constants of finite dimensional spaces. Math. Nachr., 290(16), (2017), 2547–2559.CrossRefGoogle Scholar
Carando, D. and Rodrguez, J. T.. Symmetric multilinear forms on Hilbert spaces: Where do they attain their norm? Linear Algebra Appl., 563, (2019), 178–192.CrossRefGoogle Scholar
Dineen, S.. Holomorphy types on a Banach spaces. Studia Math., 39(3), (1971), 241–288.CrossRefGoogle Scholar
Dineen, S.. Complex analysis on infinite dimensional spaces. Springer Monographs in Mathematics (London, Springer, 1999).CrossRefGoogle Scholar
Floret, K.. Natural norms on symmetric tensor products of normed spaces. Note Mat., 17, (1997), 153–188.Google Scholar
Harris, L. A.. Bounds on the derivatives of holomorphic functions of vectors. In Proc. Colloq. Analysis, Rio de Janeiro (1972), pages 145–163.Google Scholar
Kim, S. G.. Polarisation and unconditional constants of \[\mathcal{P}{(^2}{d_*}{(1,w)^2})\]. Commun. Korean Math. Soc., 29(3), (2014), 421–428.CrossRefGoogle Scholar
Kwapień, S.. Isomorphic characterisations of inner product spaces by orthogonal series with vector valued coefficients. Studia Math., 44(6), (1972), 583–595.CrossRefGoogle Scholar
Maurey, B.. Type, cotype and k-convexity. Handbook of the Geometry of Banach Spaces, 2, (2003), 1299–1332.CrossRefGoogle Scholar
Mujica, J.. Complex analysis in Banach spaces , volume 120. North-Holland Math. Stud., (1986).Google Scholar
Muñoz, G. A., Sarantopoulos, Y. and Tonge, A.. Complexifications of real Banach spaces, polynomials and multilinear maps. Studia Math., 134(1), (1999), 1–33.CrossRefGoogle Scholar
Nicodemi, O.. Homomorphisms of algebras of germs of holomorphic functions. Funct. Anal. Holomorphy and Approximation Theory 843, (1981), 534–546.CrossRefGoogle Scholar
Papadiamantis, M. K. and Sarantopoulos, Y.. Polynomial estimates on real and complex L p (μ) spaces. Studia Math., 235, (2016), 31–45.Google Scholar
Pappas, A. and Révész, S. G.. Linear polarization constants of Hilbert spaces. J. Math. Anal. Appl., 300(1), (2004), 129–146.CrossRefGoogle Scholar
Pelczynski, A. and Rosenthal, H. P.. Localisation techniques in L p spaces. Studia Math., 52(3), (1974), 263–289.Google Scholar
Revesz, S. G. and Sarantopoulos, Y.. Plank problems, polarisation and Chebyshev constants. J. Korean Math. Soc., 41(1), (2004), 157–174.CrossRefGoogle Scholar
Sarantopoulos, Y.. Estimates for polynomial norms on L p (μ) spaces. Math. Proc. Camb. Phil. Soc., 99(2), (1986), 263–271.CrossRefGoogle Scholar
Sarantopoulos, Y.. Polynomials on certain Banach spaces. Bull. Soc. Math. Greece, 28, (1987), 89–102.Google Scholar
Tomczak-Jaegermann, N.. Banach–Mazur Distances and Finite-Dimensional Operator Ideals, volume 38 (Longman Scientific & Technical, 1989).Google Scholar
Tonge, A.. Polarisation and the two-dimensional Grothendieck inequality. Math. Proc. of Camb. Phil. Soc., 95(2), (1984), 313–318.CrossRefGoogle Scholar
Varopoulos, N. T.. On an inequality of von Neumann and an application of the metric theory of tensor products to operators theory. J. Funct. Anal., 16(1), (1974), 83–100.CrossRefGoogle Scholar