Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T19:14:34.068Z Has data issue: false hasContentIssue false
  • English
  • Français

Points of egress in problems of Hamiltonian dynamics

Published online by Cambridge University Press:  24 October 2008

C. J. Amick  and
J. F. Toland
C. J. Amick
Affiliation:
Department of Mathematics, University of Chicago, Chicago, Illinois 60637, U.S.A.
J. F. Toland
Affiliation:
School of Mathematical Sciences, University of Bath, Bath, BA2 7AY
Get access Rights & Permissions [Opens in a new window]

Extract

First we consider an elementary though delicate question about the trajectory in ℝn of a particle in a conservative field of force whose dynamics are governed by the equation

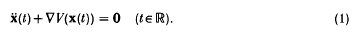
Here the potential function V is supposed to have Lipschitz continuous first derivative at every point of ℝn. This is a natural assumption which ensures that the initial-value problem is well-posed. We suppose also that there is a closed convex set C with non-empty interior C° such that V ≥ 0 in C and V = 0 on the boundary ∂C of C. It is noteworthy that we make no assumptions about the degeneracy (or otherwise) of V on ∂C (i.e. whether ∇V = 0 on ∂C, or not); thus ∂C is a Lipschitz boundary because of its convexity but not necessarily any smoother in general. We remark also that there are no convexity assumptions about V and nothing is known about the behaviour of V outside C.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 109 , Issue 2 , March 1991 , pp. 405 - 417
Copyright
Copyright © Cambridge Philosophical Society 1991

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Ekeland, I. and Aubin, J. P.. Applied Nonlinear Analysis (John Wiley, 1985).Google Scholar
[2]Hofer, H. and Toland, J. F.. Homoclinic heteroclinic and periodic orbits for a class of indefinite Hamiltonian systems. Math. Ann. 268 (1984), 387–403.CrossRefGoogle Scholar
[3]Hofer, H. and Toland, J. F.. Free oscillations of prescribed energy at a saddle-point of the potential in Hamiltonian dynamics. Delft Prog. Rep. 10 (1985), 238–249.Google Scholar
[4]Kozlov, V. V.. Calculus of variations in the large and classical mechanics. Russian Math. Surveys 40 (1985), 37–71.CrossRefGoogle Scholar
[5]Kruskal, M. and Segur, H.. Asymptotics beyond all orders in a model of crystal growth. To appear in Studies in Applied Math.Google Scholar
[6]Toland, J. F.. Periodic solutions for a class of Lorenz–Lagrangian systems. Ann. Inst. H. Poincaré Anal. Non Linéaire 5 (1988), 211–220.CrossRefGoogle Scholar