Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T05:10:50.616Z Has data issue: false hasContentIssue false
  • English
  • Français

Planar threefolds in space of four dimensions

Published online by Cambridge University Press:  24 October 2008

W. G. Welchman
W. G. Welchman
Affiliation:
Sidney Sussex College
Get access Rights & Permissions [Opens in a new window]

Extract

1. It is known that, in [3], a ruled surface of order n and genus p has in general a double curve of order ½ (n − 1) (n − 2) − p and genus ½ (n − 5) (n + 2p − 2) + 1, 2(n + 2p − 2) torsal generators, 2(n − 2)(n − 3) − 2(n − 6)p generators which touch the double curve, and 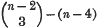triple points.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 29 , Issue 1 , January 1933 , pp. 103 - 115
Copyright
Copyright © Cambridge Philosophical Society 1933

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* See, for instance, Edge, , Ruled Surfaces, 28–31.Google Scholar

* Roth, L., Proc. London Math. Soc. (2), 33 (1932), 115–144.CrossRefGoogle Scholar

† See Edge, loc. cit.

* For a complete discussion of tangent spaces of manifolds generated by spaces see Segre, , Rend. Palermo, 30 (1910), 87.CrossRefGoogle Scholar

† See, for instance, Segre, , Encykl. Math. Wiss., iii c 7, 913Google Scholar. See also § 8.

‡ Rend. Palermo, 3 (1889), 27Google Scholar. See also § 9.

§ For the results dual to these see Todd, , Proc. Lond. Math. Soc. (2), 30 (1930), 513–550 (530).CrossRefGoogle Scholar

* This shows again that each plane of meets Γ in points.

* See, for instance, Seven, , Geometria algebrica, i, 1, Bologna (1926), 228.Google Scholar

† I.e. if the fourfold point is not a torsal point or a point of contact of a tangent plane.

* See § 3.

† A focus of order λ is a point of intersection of λ + 1 consecutive generating spaces.

* For a complete discussion see Edge, Ruled Surfaces, p. 36. Non-rational ruled surfaces are discussed by Segre, , Math. Ann. 34 (1889), 1.CrossRefGoogle Scholar

* These results are proved by Segre, , Atti Acc. Torino, 21 (1885), 95Google Scholar. Non-rational manifolds generated by ∞1 planes are discussed by Pagliano, , Annali di Mat. (3), 5 (1901), 77.CrossRefGoogle Scholar

† This is the well-known of [5] generated by the planes which meet four lines.

* See Segre, loc. cit.