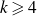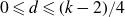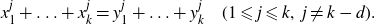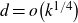1. Introduction
Recent progress on Vinogradov’s mean value theorem has resolved the main conjecture in the subject. Thus, writing
![]() $J_{s,k}(X)$
for the number of integral solutions of the system of equations
$J_{s,k}(X)$
for the number of integral solutions of the system of equations
with
![]() $1\leqslant x_i,y_i\leqslant X$
$1\leqslant x_i,y_i\leqslant X$
![]() $(1\leqslant i\leqslant s)$
, it is now known that whenever
$(1\leqslant i\leqslant s)$
, it is now known that whenever
![]() $\varepsilon>0$
, one has
$\varepsilon>0$
, one has
(see [
Reference Bourgain, Demeter and Guth1
] or [
Reference Wooley13
,
Reference Wooley14
]). Denote by
![]() $T_s(X)$
the number of s-tuples
$T_s(X)$
the number of s-tuples
![]() ${{\textbf{x}}}$
and
${{\textbf{x}}}$
and
![]() ${\textbf{y}}$
in which
${\textbf{y}}$
in which
![]() $1\leqslant x_i,y_i\leqslant X$
$1\leqslant x_i,y_i\leqslant X$
![]() $(1\leqslant i\leqslant s)$
, and
$(1\leqslant i\leqslant s)$
, and
![]() $(x_1,\ldots ,x_s)$
is a permutation of
$(x_1,\ldots ,x_s)$
is a permutation of
![]() $(y_1,\ldots ,y_s)$
. Thus
$(y_1,\ldots ,y_s)$
. Thus
![]() $T_s(X)=s!X^s+O(X^{s-1})$
. A conjecture going beyond the main conjecture (1·2) asserts that when
$T_s(X)=s!X^s+O(X^{s-1})$
. A conjecture going beyond the main conjecture (1·2) asserts that when
![]() $1\leqslant s<\tfrac{1}{2}k(k+1)$
, one should have
$1\leqslant s<\tfrac{1}{2}k(k+1)$
, one should have
This conclusion is essentially trivial for
![]() $1\leqslant s\leqslant k$
, in which circumstances one has the definitive statement
$1\leqslant s\leqslant k$
, in which circumstances one has the definitive statement
![]() $J_{s,k}(X)=T_s(X)$
. When
$J_{s,k}(X)=T_s(X)$
. When
![]() $s\geqslant k+2$
, meanwhile, the conclusion (1·3) is at present far beyond our grasp. This leaves the special case
$s\geqslant k+2$
, meanwhile, the conclusion (1·3) is at present far beyond our grasp. This leaves the special case
![]() $s=k+1$
. Here, one has the asymptotic relation
$s=k+1$
. Here, one has the asymptotic relation
established in joint work of the author with Vaughan [
Reference Vaughan and Wooley10
, theorem 1]. An analogous conclusion is available when the equation of degree
![]() $k-1$
in the system (1·1) is removed, but in no other close relative of Vinogradov’s mean value theorem has such a conclusion been obtained hitherto. Our purpose in this paper is to derive estimates of strength paralleling (1·4) in systems of the shape (1·1) in which a large degree equation is removed.
$k-1$
in the system (1·1) is removed, but in no other close relative of Vinogradov’s mean value theorem has such a conclusion been obtained hitherto. Our purpose in this paper is to derive estimates of strength paralleling (1·4) in systems of the shape (1·1) in which a large degree equation is removed.
In order to describe our conclusions, we must introduce some notation. When
![]() $k\geqslant 2$
and
$k\geqslant 2$
and
![]() $0\leqslant d<k$
, we denote by
$0\leqslant d<k$
, we denote by
![]() $I_{k,d}(X)$
the number of integral solutions of the system of equations
$I_{k,d}(X)$
the number of integral solutions of the system of equations
with
![]() $1\leqslant x_i,y_i\leqslant X$
$1\leqslant x_i,y_i\leqslant X$
![]() $(1\leqslant i\leqslant k)$
. Also, when
$(1\leqslant i\leqslant k)$
. Also, when
![]() $k\geqslant 3$
and
$k\geqslant 3$
and
![]() $d\geqslant 0$
, we define the exponent
$d\geqslant 0$
, we define the exponent
Theorem 1·1.
Suppose that
![]() $k\geqslant 3$
and
$k\geqslant 3$
and
![]() $0\leqslant d<k/2$
. Then, for each
$0\leqslant d<k/2$
. Then, for each
![]() $\varepsilon>0$
, one has
$\varepsilon>0$
, one has
When k is large and d is small compared to k, the conclusion of this theorem provides strikingly powerful paucity estimates.
Corollary 1·2.
Suppose that
![]() $d\leqslant \sqrt{k}$
. Then
$d\leqslant \sqrt{k}$
. Then
In particular, when
![]() $d=o\!\left(k^{1/4}\right)$
, one has
$d=o\!\left(k^{1/4}\right)$
, one has
Although for larger values of d our paucity estimates become weaker, they remain non-trivial whenever
![]() $d<(k-2)/4$
.
$d<(k-2)/4$
.
Corollary 1·3.
Provided that
![]() $d\geqslant 1$
and
$d\geqslant 1$
and
![]() $k\geqslant 4d+3$
, one has
$k\geqslant 4d+3$
, one has
Moreover, when
![]() $1\leqslant d\leqslant k/4$
, one has
$1\leqslant d\leqslant k/4$
, one has
so that whenever
![]() $\eta$
is small and positive, and
$\eta$
is small and positive, and
![]() $1\leqslant d\leqslant \eta^2 k$
, then
$1\leqslant d\leqslant \eta^2 k$
, then
Previous work on this problem is confined to the two cases considered by Hua [
Reference Hua4
, lemmata 5·2 and 5·4]. Thus, the asymptotic formula (1·4) derived by the author jointly with Vaughan [
Reference Vaughan and Wooley10
, theorem 1] is tantamount to the case
![]() $d=0$
of Theorem 1·1. Meanwhile, it follows from [
Reference Vaughan and Wooley10
, theorem 2] that
$d=0$
of Theorem 1·1. Meanwhile, it follows from [
Reference Vaughan and Wooley10
, theorem 2] that
and the error term here is slightly sharper than that provided by the case
![]() $d=1$
of Theorem 1·1. The conclusion of Theorem 1·1 is new whenever
$d=1$
of Theorem 1·1. The conclusion of Theorem 1·1 is new whenever
![]() $d\geqslant 2$
. It would be interesting to derive analogues of Theorem 1·1 in which more than one equation is removed from the Vinogradov system (1·1), or indeed to derive analogues in which the number of variables is increased and yet one is able nonetheless to confirm the paucity of non-diagonal solutions. We have more to say on such matters in Section 5 of this paper. For now, we confine ourselves to remarking that when many, or even most, lower degree equations are removed, then approaches based on the determinant method are available. Consider, for example, natural numbers
$d\geqslant 2$
. It would be interesting to derive analogues of Theorem 1·1 in which more than one equation is removed from the Vinogradov system (1·1), or indeed to derive analogues in which the number of variables is increased and yet one is able nonetheless to confirm the paucity of non-diagonal solutions. We have more to say on such matters in Section 5 of this paper. For now, we confine ourselves to remarking that when many, or even most, lower degree equations are removed, then approaches based on the determinant method are available. Consider, for example, natural numbers
![]() $d_1,\ldots ,d_k$
with
$d_1,\ldots ,d_k$
with
![]() $1\leqslant d_1<d_2<\ldots <d_k$
and
$1\leqslant d_1<d_2<\ldots <d_k$
and
![]() $d_k\geqslant 2s-1$
. Also, denote by
$d_k\geqslant 2s-1$
. Also, denote by
![]() $M_{{{\textbf{d}}},s}(X)$
the number of integral solutions of the system of equations
$M_{{{\textbf{d}}},s}(X)$
the number of integral solutions of the system of equations
with
![]() $1\leqslant x_i,y_i\leqslant X$
$1\leqslant x_i,y_i\leqslant X$
![]() $(1\leqslant i\leqslant s)$
. Then it follows from [
Reference Salberger and Wooley7
, theorem 5·2] that whenever
$(1\leqslant i\leqslant s)$
. Then it follows from [
Reference Salberger and Wooley7
, theorem 5·2] that whenever
![]() $d_1\cdots d_k\geqslant (2s-k)^{4s-2k}$
, one has
$d_1\cdots d_k\geqslant (2s-k)^{4s-2k}$
, one has
The proof of Theorem 1·1, in common with our earlier treatment in [
Reference Vaughan and Wooley10
] of the Vinogradov system (1·1), is based on the application of multiplicative polynomial identities amongst variables in pursuit of parametrisations that these days would be described as being of torsorial type. The key innovation of [
Reference Vaughan and Wooley10
] was to relate not merely two product polynomials, but instead
![]() $r\geqslant 2$
such polynomials, leading to a decomposition of the variables into
$r\geqslant 2$
such polynomials, leading to a decomposition of the variables into
![]() $(k+1)^r$
parameters. Large numbers of these parameters may be determined via divisor function estimates, and thereby one obtains powerful bounds for the difference
$(k+1)^r$
parameters. Large numbers of these parameters may be determined via divisor function estimates, and thereby one obtains powerful bounds for the difference
![]() $J_{k+1,k}(X)-T_{k+1}(X)$
. In the present situation, the polynomial identities are more novel, and sacrifices must be made in order to bring an analogous plan to fruition. Nonetheless, when
$J_{k+1,k}(X)-T_{k+1}(X)$
. In the present situation, the polynomial identities are more novel, and sacrifices must be made in order to bring an analogous plan to fruition. Nonetheless, when
![]() $d<k/2$
, the kind of multiplicative relations of [
Reference Vaughan and Wooley10
] may still be derived in a useful form.
$d<k/2$
, the kind of multiplicative relations of [
Reference Vaughan and Wooley10
] may still be derived in a useful form.
This paper is organised as follows. We begin in Section 2 of this paper by deriving the polynomial identities required for our subsequent analysis. In Section 3 we refine this infrastructure so that appropriate multiplicative relations are obtained involving few auxiliary variables. A complication for us here is the problem of bounding the number of choices for these auxiliary variables, since they are of no advantage to us in the ensuing analysis of multiplicative relations. In Section 4, we exploit the multiplicative relations by extracting common divisors between tuples of variables, following the path laid down in our earlier work with Vaughan [ Reference Vaughan and Wooley10 ]. This leads to the proof of Theorem 1·1. Finally, in Section 5, we discuss the corollaries to Theorem 1·1 and consider also refinements and potential generalisations of our main results.
Our basic parameter is X, a sufficiently large positive number. Whenever
![]() $\varepsilon$
appears in a statement, either implicitly or explicitly, we assert that the statement holds for each
$\varepsilon$
appears in a statement, either implicitly or explicitly, we assert that the statement holds for each
![]() $\varepsilon>0$
. In this paper, implicit constants in Vinogradov’s notation
$\varepsilon>0$
. In this paper, implicit constants in Vinogradov’s notation
![]() $\ll$
and
$\ll$
and
![]() $\gg$
may depend on
$\gg$
may depend on
![]() $\varepsilon$
, k, and s. We make frequent use of vector notation in the form
$\varepsilon$
, k, and s. We make frequent use of vector notation in the form
![]() ${{\textbf{x}}}=(x_1,\ldots,x_r)$
. Here, the dimension r depends on the course of the argument. We also write
${{\textbf{x}}}=(x_1,\ldots,x_r)$
. Here, the dimension r depends on the course of the argument. We also write
![]() $(a_1,\ldots ,a_s)$
for the greatest common divisor of the integers
$(a_1,\ldots ,a_s)$
for the greatest common divisor of the integers
![]() $a_1,\ldots ,a_s$
. Any ambiguity between ordered s-tuples and corresponding greatest common divisors will be easily resolved by context. Finally, as usual, we write e(z) for
$a_1,\ldots ,a_s$
. Any ambiguity between ordered s-tuples and corresponding greatest common divisors will be easily resolved by context. Finally, as usual, we write e(z) for
![]() $e^{2\pi iz}$
.
$e^{2\pi iz}$
.
2. Polynomial identities
We begin by introducing the power sum polynomials
On recalling (1·5), we see that
![]() $I_{k,d}(X)$
counts the number of integral solutions of the system of equations
$I_{k,d}(X)$
counts the number of integral solutions of the system of equations
 \begin{equation}\left.\begin{aligned}s_j({{\textbf{x}}})&=s_j({\textbf{y}})\quad (1\leqslant j\leqslant k,\, j\ne k-d)\\s_{k-d}({{\textbf{x}}})&=s_{k-d}({\textbf{y}})+h,\end{aligned}\right\}\end{equation}
\begin{equation}\left.\begin{aligned}s_j({{\textbf{x}}})&=s_j({\textbf{y}})\quad (1\leqslant j\leqslant k,\, j\ne k-d)\\s_{k-d}({{\textbf{x}}})&=s_{k-d}({\textbf{y}})+h,\end{aligned}\right\}\end{equation}
with
![]() $1\leqslant {{\textbf{x}}},{\textbf{y}}\leqslant X$
and
$1\leqslant {{\textbf{x}}},{\textbf{y}}\leqslant X$
and
![]() $|h|\leqslant kX^{k-d}$
. Our first task is to reinterpret this system in terms of elementary symmetric polynomials, so that our first multiplicative relations may be extracted.
$|h|\leqslant kX^{k-d}$
. Our first task is to reinterpret this system in terms of elementary symmetric polynomials, so that our first multiplicative relations may be extracted.
The elementary symmetric polynomials
![]() ${\sigma}_j({{\textbf{z}}})\in {\mathbb Z}[z_1,\ldots ,z_k]$
may be defined by means of the generating function identity
${\sigma}_j({{\textbf{z}}})\in {\mathbb Z}[z_1,\ldots ,z_k]$
may be defined by means of the generating function identity
 \begin{align*}1+\sum_{j=1}^k{\sigma}_j({{\textbf{z}}})({-}t)^j=\prod_{i=1}^k(1-tz_i).\end{align*}
\begin{align*}1+\sum_{j=1}^k{\sigma}_j({{\textbf{z}}})({-}t)^j=\prod_{i=1}^k(1-tz_i).\end{align*}
Since
 \begin{align*}\sum_{i=1}^k\log\! (1-tz_i)=-\sum_{j=1}^\infty s_j({{\textbf{z}}})\frac{t^j}{j},\end{align*}
\begin{align*}\sum_{i=1}^k\log\! (1-tz_i)=-\sum_{j=1}^\infty s_j({{\textbf{z}}})\frac{t^j}{j},\end{align*}
we deduce that
 \begin{align*}1+\sum_{j=1}^k{\sigma}_j({{\textbf{z}}})({-}t)^j=\exp \!\left( -\sum_{j=1}^\infty s_j({{\textbf{z}}})\frac{t^j}{j}\right) .\end{align*}
\begin{align*}1+\sum_{j=1}^k{\sigma}_j({{\textbf{z}}})({-}t)^j=\exp \!\left( -\sum_{j=1}^\infty s_j({{\textbf{z}}})\frac{t^j}{j}\right) .\end{align*}
When
![]() $n\geqslant 1$
, the formula
$n\geqslant 1$
, the formula
 \begin{equation}{\sigma}_n({{\textbf{z}}})=({-}1)^n\sum_{\substack{m_1+2m_2+\ldots +nm_n=n\\ m_i\geqslant 0}}\,\prod_{i=1}^n \frac{({-}s_i({{\textbf{z}}}))^{m_i}}{i^{m_i}m_i!}\end{equation}
\begin{equation}{\sigma}_n({{\textbf{z}}})=({-}1)^n\sum_{\substack{m_1+2m_2+\ldots +nm_n=n\\ m_i\geqslant 0}}\,\prod_{i=1}^n \frac{({-}s_i({{\textbf{z}}}))^{m_i}}{i^{m_i}m_i!}\end{equation}
then follows via an application of Faà di Bruno’s formula. By convention, we put
![]() ${\sigma}_0({{\textbf{z}}})=1$
. We refer the reader to [
Reference MacDonald5
, equation (2·14
${\sigma}_0({{\textbf{z}}})=1$
. We refer the reader to [
Reference MacDonald5
, equation (2·14
![]() $^\prime$
)] for a self-contained account of the relation (2·2).
$^\prime$
)] for a self-contained account of the relation (2·2).
Suppose now that
![]() $0\leqslant d<k/2$
, and that the integers
$0\leqslant d<k/2$
, and that the integers
![]() ${{\textbf{x}}},{\textbf{y}},h$
satisfy (2·1). When
${{\textbf{x}}},{\textbf{y}},h$
satisfy (2·1). When
![]() $1\leqslant n<k-d$
, it follows from (2·2) that
$1\leqslant n<k-d$
, it follows from (2·2) that
 \begin{equation}{\sigma}_n({{\textbf{x}}})=({-}1)^n\sum_{\substack{m_1+2m_2+\ldots +nm_n=n\\ m_i\geqslant 0}}\,\prod_{i=1}^n \frac{({-}s_i({\textbf{y}}))^{m_i}}{i^{m_i}m_i!}={\sigma}_n({\textbf{y}}).\end{equation}
\begin{equation}{\sigma}_n({{\textbf{x}}})=({-}1)^n\sum_{\substack{m_1+2m_2+\ldots +nm_n=n\\ m_i\geqslant 0}}\,\prod_{i=1}^n \frac{({-}s_i({\textbf{y}}))^{m_i}}{i^{m_i}m_i!}={\sigma}_n({\textbf{y}}).\end{equation}
When
![]() $k-d\leqslant n\leqslant k$
, on the other hand, we instead obtain the relation
$k-d\leqslant n\leqslant k$
, on the other hand, we instead obtain the relation
 \begin{align*}{\sigma}_n({{\textbf{x}}})=({-}1)^n\sum_{\substack{m_1+2m_2+\ldots +nm_n=n\\ m_i\geqslant 0}}\,\frac{({-}s_{k-d}({\textbf{y}})-h)^{m_{k-d}}}{(k-d)^{m_{k-d}}m_{k-d}!}\prod_{\substack{1\leqslant i\leqslant n\\ i\ne k-d}}\frac{({-}s_i({\textbf{y}}))^{m_i}}{i^{m_i}m_i!} .\end{align*}
\begin{align*}{\sigma}_n({{\textbf{x}}})=({-}1)^n\sum_{\substack{m_1+2m_2+\ldots +nm_n=n\\ m_i\geqslant 0}}\,\frac{({-}s_{k-d}({\textbf{y}})-h)^{m_{k-d}}}{(k-d)^{m_{k-d}}m_{k-d}!}\prod_{\substack{1\leqslant i\leqslant n\\ i\ne k-d}}\frac{({-}s_i({\textbf{y}}))^{m_i}}{i^{m_i}m_i!} .\end{align*}
Since
![]() $d<k/2$
, the summation condition on
$d<k/2$
, the summation condition on
![]() ${{\textbf{m}}}$
ensures that
${{\textbf{m}}}$
ensures that
![]() $m_{k-d}\in \{0,1\}$
. Thus, by isolating the term in which
$m_{k-d}\in \{0,1\}$
. Thus, by isolating the term in which
![]() $m_{k-d}=1$
, we see that
$m_{k-d}=1$
, we see that
where, by (2·2),
 \begin{align*}\psi_n({\textbf{y}})&=\frac{({-}1)^{n+1}}{k-d}\sum_{\substack{m_1+2m_2+\ldots +(n-k+d)m_{n-k+d}=n-k+d\\ m_i\geqslant 0}}\prod_{i=1}^{n-k+d}\frac{({-}s_i({\textbf{y}}))^{m_i}}{i^{m_i}m_i!}\\&=\frac{({-}1)^{k-d+1}}{k-d}{\sigma}_{n-k+d}({\textbf{y}}).\end{align*}
\begin{align*}\psi_n({\textbf{y}})&=\frac{({-}1)^{n+1}}{k-d}\sum_{\substack{m_1+2m_2+\ldots +(n-k+d)m_{n-k+d}=n-k+d\\ m_i\geqslant 0}}\prod_{i=1}^{n-k+d}\frac{({-}s_i({\textbf{y}}))^{m_i}}{i^{m_i}m_i!}\\&=\frac{({-}1)^{k-d+1}}{k-d}{\sigma}_{n-k+d}({\textbf{y}}).\end{align*}
We deduce from (2·3) and (2·4) that
 \begin{align}\prod_{i=1}^k(t-x_i)-\prod_{i=1}^k(t-y_i)&=({-}1)^k\sum_{n=0}^k({\sigma}_n({{\textbf{x}}})-{\sigma}_n({\textbf{y}}))({-}t)^{k-n}\notag \\&=({-}1)^{d-1}\frac{h}{k-d}\sum_{m=0}^d{\sigma}_m({\textbf{y}})({-}t)^{d-m}.\end{align}
\begin{align}\prod_{i=1}^k(t-x_i)-\prod_{i=1}^k(t-y_i)&=({-}1)^k\sum_{n=0}^k({\sigma}_n({{\textbf{x}}})-{\sigma}_n({\textbf{y}}))({-}t)^{k-n}\notag \\&=({-}1)^{d-1}\frac{h}{k-d}\sum_{m=0}^d{\sigma}_m({\textbf{y}})({-}t)^{d-m}.\end{align}
Define the polynomial
 \begin{equation}\tau_d({\textbf{y}};\,w)=({-}1)^{d-1}\sum_{m=0}^d{\sigma}_m({\textbf{y}})({-}w)^{d-m}.\end{equation}
\begin{equation}\tau_d({\textbf{y}};\,w)=({-}1)^{d-1}\sum_{m=0}^d{\sigma}_m({\textbf{y}})({-}w)^{d-m}.\end{equation}
Then we deduce from (2·5) that for
![]() $1\leqslant j\leqslant k$
, one has the relation
$1\leqslant j\leqslant k$
, one has the relation
 \begin{equation}(k-d)\prod_{i=1}^k(y_j-x_i)=\tau_d({\textbf{y}};\,y_j)h.\end{equation}
\begin{equation}(k-d)\prod_{i=1}^k(y_j-x_i)=\tau_d({\textbf{y}};\,y_j)h.\end{equation}
By comparing the relation (2·7) with
![]() $j=s$
and
$j=s$
and
![]() $j=t$
for two distinct indices s and t satisfying
$j=t$
for two distinct indices s and t satisfying
![]() $1\leqslant s<t\leqslant k$
, it is apparent that
$1\leqslant s<t\leqslant k$
, it is apparent that
 \begin{equation}\tau_d({\textbf{y}};\,y_t)\prod_{i=1}^k(y_s-x_i)=\tau_d({\textbf{y}};\,y_s)\prod_{i=1}^k(y_t-x_i).\end{equation}
\begin{equation}\tau_d({\textbf{y}};\,y_t)\prod_{i=1}^k(y_s-x_i)=\tau_d({\textbf{y}};\,y_s)\prod_{i=1}^k(y_t-x_i).\end{equation}
Furthermore, by applying the relations (2·3), we see that
![]() ${\sigma}_m({\textbf{y}})={\sigma}_m({{\textbf{x}}})$
for
${\sigma}_m({\textbf{y}})={\sigma}_m({{\textbf{x}}})$
for
![]() $1\leqslant m\leqslant d$
, and thus it is a consequence of (2·6) that
$1\leqslant m\leqslant d$
, and thus it is a consequence of (2·6) that
We therefore deduce from (2·8) that for
![]() $1\leqslant s<t\leqslant k$
, one has
$1\leqslant s<t\leqslant k$
, one has
 \begin{equation}\tau_d({{\textbf{x}}};\,y_t)\prod_{i=1}^k(y_s-x_i)=\tau_d({{\textbf{x}}};\,y_s)\prod_{i=1}^k(y_t-x_i).\end{equation}
\begin{equation}\tau_d({{\textbf{x}}};\,y_t)\prod_{i=1}^k(y_s-x_i)=\tau_d({{\textbf{x}}};\,y_s)\prod_{i=1}^k(y_t-x_i).\end{equation}
These are the multiplicative relations that provide the foundation for our analysis. One additional detail shall detain us temporarily, however, for to be useful we must ensure that all of the factors on left- and right-hand sides of (2·8) and (2·10) are non-zero.
Suppose temporarily that there are indices l and m with
![]() $1\leqslant l,m\leqslant k$
for which
$1\leqslant l,m\leqslant k$
for which
![]() $x_l=y_m$
. By relabelling variables, if necessary, we may suppose that
$x_l=y_m$
. By relabelling variables, if necessary, we may suppose that
![]() $l=m=k$
, and then it follows from (2·1) that
$l=m=k$
, and then it follows from (2·1) that
There are
![]() $k-1$
equations here in
$k-1$
equations here in
![]() $k-1$
pairs of variables
$k-1$
pairs of variables
![]() $x_i,y_i$
, and thus it follows from [
Reference Steinig9
] that
$x_i,y_i$
, and thus it follows from [
Reference Steinig9
] that
![]() $(x_1,\ldots ,x_{k-1})$
is a permutation of
$(x_1,\ldots ,x_{k-1})$
is a permutation of
![]() $(y_1,\ldots ,y_{k-1})$
. We may therefore conclude that in the situation contemplated at the beginning of this paragraph, the solution
$(y_1,\ldots ,y_{k-1})$
. We may therefore conclude that in the situation contemplated at the beginning of this paragraph, the solution
![]() ${{\textbf{x}}},{\textbf{y}}$
of (2·1) is counted by
${{\textbf{x}}},{\textbf{y}}$
of (2·1) is counted by
![]() $T_k(X)$
, with
$T_k(X)$
, with
![]() $(x_1,\ldots ,x_k)$
a permutation of
$(x_1,\ldots ,x_k)$
a permutation of
![]() $(y_1,\ldots ,y_k)$
. In particular, in any solution
$(y_1,\ldots ,y_k)$
. In particular, in any solution
![]() ${{\textbf{x}}},{\textbf{y}}$
of (2·1) counted by
${{\textbf{x}}},{\textbf{y}}$
of (2·1) counted by
![]() $I_{k,d}(X)-T_k(X)$
, it follows that
$I_{k,d}(X)-T_k(X)$
, it follows that
![]() $x_l=y_m$
for no indices l and m satisfying
$x_l=y_m$
for no indices l and m satisfying
![]() $1\leqslant l,m\leqslant k$
. In view of (2·7) and (2·9), such solutions also satisfy the conditions
$1\leqslant l,m\leqslant k$
. In view of (2·7) and (2·9), such solutions also satisfy the conditions
We summarise the deliberations of this section in the form of a lemma.
3. Reduction to efficient multiplicative relations
We seek to estimate the number
![]() $I_{k,d}(X)-T_k(X)$
of solutions of the system (2·1), with
$I_{k,d}(X)-T_k(X)$
of solutions of the system (2·1), with
![]() $1\leqslant {{\textbf{x}}},{\textbf{y}}\leqslant X$
and
$1\leqslant {{\textbf{x}}},{\textbf{y}}\leqslant X$
and
![]() $|h|\leqslant kX^{k-d}$
, for which
$|h|\leqslant kX^{k-d}$
, for which
![]() $(x_1,\ldots ,x_k)$
is not a permutation of
$(x_1,\ldots ,x_k)$
is not a permutation of
![]() $(y_1,\ldots ,y_k)$
. We divide these solutions into two types according to a parameter r with
$(y_1,\ldots ,y_k)$
. We divide these solutions into two types according to a parameter r with
![]() $1<r\leqslant k$
. Let
$1<r\leqslant k$
. Let
![]() $V_{1,r}(X)$
denote the number of such solutions in which there are fewer than r distinct values amongst
$V_{1,r}(X)$
denote the number of such solutions in which there are fewer than r distinct values amongst
![]() $x_1,\ldots ,x_k$
, and likewise fewer than r distinct values amongst
$x_1,\ldots ,x_k$
, and likewise fewer than r distinct values amongst
![]() $y_1,\ldots ,y_k$
. Also, let
$y_1,\ldots ,y_k$
. Also, let
![]() $V_{2,r}(X)$
denote the corresponding number of solutions in which there are either at least r distinct values amongst
$V_{2,r}(X)$
denote the corresponding number of solutions in which there are either at least r distinct values amongst
![]() $x_1,\ldots ,x_k$
, or at least r distinct values amongst
$x_1,\ldots ,x_k$
, or at least r distinct values amongst
![]() $y_1,\ldots ,y_k$
. Then one has
$y_1,\ldots ,y_k$
. Then one has
The solutions counted by
![]() $V_{1,r}(X)$
are easily handled via an expedient argument of circle method flavour.
$V_{1,r}(X)$
are easily handled via an expedient argument of circle method flavour.
Lemma 3·1.
One has
![]() $V_{1,r}(X)\ll X^{r-1}$
.
$V_{1,r}(X)\ll X^{r-1}$
.
Proof. It is convenient to introduce the exponential sum
 \begin{align*}f({\boldsymbol \alpha})=\sum_{1\leqslant x\leqslant X}e\!\left( \sum_{\substack{1\leqslant j\leqslant k\\ j\ne k-d}}{\alpha}_jx^j\right) .\end{align*}
\begin{align*}f({\boldsymbol \alpha})=\sum_{1\leqslant x\leqslant X}e\!\left( \sum_{\substack{1\leqslant j\leqslant k\\ j\ne k-d}}{\alpha}_jx^j\right) .\end{align*}
In a typical solution
![]() ${{\textbf{x}}},{\textbf{y}}$
of (2·1) counted by
${{\textbf{x}}},{\textbf{y}}$
of (2·1) counted by
![]() $V_{1,r}(X)$
, we may relabel indices in such a manner that
$V_{1,r}(X)$
, we may relabel indices in such a manner that
![]() $x_j\in \{x_1,\ldots ,x_{r-1}\}$
for
$x_j\in \{x_1,\ldots ,x_{r-1}\}$
for
![]() $1\leqslant j\leqslant k$
, and likewise
$1\leqslant j\leqslant k$
, and likewise
![]() $y_j\in \{y_1,\ldots ,y_{r-1}\}$
for
$y_j\in \{y_1,\ldots ,y_{r-1}\}$
for
![]() $1\leqslant j\leqslant k$
. On absorbing combinatorial factors into the constant implicit in the notation of Vinogradov, therefore, we discern via orthogonality that there are integers
$1\leqslant j\leqslant k$
. On absorbing combinatorial factors into the constant implicit in the notation of Vinogradov, therefore, we discern via orthogonality that there are integers
![]() $a_i,b_i$
$a_i,b_i$
![]() $(1\leqslant i\leqslant r-1)$
, with
$(1\leqslant i\leqslant r-1)$
, with
![]() $1\leqslant a_i,b_i\leqslant k$
, for which one has
$1\leqslant a_i,b_i\leqslant k$
, for which one has
 \begin{align*}V_{1,r}(X)\ll \int_{[0,1)^{k-1}}\Biggl( \prod_{i=1}^{r-1}f(a_i{\boldsymbol \alpha})f({-}b_i{\boldsymbol \alpha})\Biggr){\,{\text{d}}}{\boldsymbol \alpha} .\end{align*}
\begin{align*}V_{1,r}(X)\ll \int_{[0,1)^{k-1}}\Biggl( \prod_{i=1}^{r-1}f(a_i{\boldsymbol \alpha})f({-}b_i{\boldsymbol \alpha})\Biggr){\,{\text{d}}}{\boldsymbol \alpha} .\end{align*}
An application of Hölder’s inequality shows that
 \begin{align*}V_{1,r}(X)\ll \prod_{i=1}^{r-1}I(a_i)^{1/(2r-2)}I(b_i)^{1/(2r-2)},\end{align*}
\begin{align*}V_{1,r}(X)\ll \prod_{i=1}^{r-1}I(a_i)^{1/(2r-2)}I(b_i)^{1/(2r-2)},\end{align*}
where we write
Thus, by making a change of variables, we discern that
By orthogonality, the latter mean value counts the integral solutions of the system
with
![]() $1\leqslant {{\textbf{x}}},{\textbf{y}}\leqslant X$
. Since the number of equations here is
$1\leqslant {{\textbf{x}}},{\textbf{y}}\leqslant X$
. Since the number of equations here is
![]() $k-1$
, and the number of pairs of variables is
$k-1$
, and the number of pairs of variables is
![]() $r-1\leqslant k-1$
, it follows from [
Reference Steinig9
] that
$r-1\leqslant k-1$
, it follows from [
Reference Steinig9
] that
![]() $(x_1,\ldots ,x_{r-1})$
is a permutation of
$(x_1,\ldots ,x_{r-1})$
is a permutation of
![]() $(y_1,\ldots ,y_{r-1})$
, and hence we deduce that
$(y_1,\ldots ,y_{r-1})$
, and hence we deduce that
This establishes the upper bound claimed in the statement of the lemma.
We next consider the solutions
![]() ${{\textbf{x}}},{\textbf{y}},h$
of the system (2·1) counted by
${{\textbf{x}}},{\textbf{y}},h$
of the system (2·1) counted by
![]() $V_{2,r}(X)$
. Here, by taking advantage of the symmetry between
$V_{2,r}(X)$
. Here, by taking advantage of the symmetry between
![]() ${{\textbf{x}}}$
and
${{\textbf{x}}}$
and
![]() ${\textbf{y}}$
, and if necessary relabelling indices, we may suppose that
${\textbf{y}}$
, and if necessary relabelling indices, we may suppose that
![]() $y_1,\ldots ,y_r$
are distinct. Suppose temporarily that the integers
$y_1,\ldots ,y_r$
are distinct. Suppose temporarily that the integers
![]() $y_t$
and
$y_t$
and
![]() $x_i-y_t$
have been determined for
$x_i-y_t$
have been determined for
![]() $1\leqslant i\leqslant k$
and
$1\leqslant i\leqslant k$
and
![]() $1\leqslant t\leqslant r$
. It follows that
$1\leqslant t\leqslant r$
. It follows that
![]() $y_t$
and
$y_t$
and
![]() $x_i$
are determined for
$x_i$
are determined for
![]() $1\leqslant i\leqslant k$
and
$1\leqslant i\leqslant k$
and
![]() $1\leqslant t\leqslant r$
, and hence also that the coefficients
$1\leqslant t\leqslant r$
, and hence also that the coefficients
![]() ${\sigma}_m({{\textbf{x}}})$
of the polynomial
${\sigma}_m({{\textbf{x}}})$
of the polynomial
![]() $\tau_d({{\textbf{x}}};\,w)$
are fixed for
$\tau_d({{\textbf{x}}};\,w)$
are fixed for
![]() $0\leqslant m\leqslant d$
. The integers
$0\leqslant m\leqslant d$
. The integers
![]() $y_s$
for
$y_s$
for
![]() $r<s\leqslant k$
may consequently be determined from the polynomial equations (2·10) with
$r<s\leqslant k$
may consequently be determined from the polynomial equations (2·10) with
![]() $t=1$
. Here, it is useful to observe that with
$t=1$
. Here, it is useful to observe that with
![]() $y_1$
and
$y_1$
and
![]() $x_1,\ldots ,x_k$
already fixed, and all the factors on the left- and right-hand side of (2·10) non-zero, the equation (2·10) becomes a polynomial in the single variable
$x_1,\ldots ,x_k$
already fixed, and all the factors on the left- and right-hand side of (2·10) non-zero, the equation (2·10) becomes a polynomial in the single variable
![]() $y_s$
. On the left-hand side one has a polynomial of degree k, whilst on the right-hand side the polynomial has degree
$y_s$
. On the left-hand side one has a polynomial of degree k, whilst on the right-hand side the polynomial has degree
![]() $d=\text{deg}_y(\tau_d({{\textbf{x}}};\,y))<k$
. Thus
$d=\text{deg}_y(\tau_d({{\textbf{x}}};\,y))<k$
. Thus
![]() $y_s$
is determined by a polynomial of degree k to which there are at most k solutions. Given fixed choices for
$y_s$
is determined by a polynomial of degree k to which there are at most k solutions. Given fixed choices for
![]() $y_t$
and
$y_t$
and
![]() $x_i-y_t$
for
$x_i-y_t$
for
![]() $1\leqslant i\leqslant k$
and
$1\leqslant i\leqslant k$
and
![]() $1\leqslant t\leqslant r$
, therefore, there are O(1) possible choices for
$1\leqslant t\leqslant r$
, therefore, there are O(1) possible choices for
![]() $y_{r+1},\ldots ,y_k$
.
$y_{r+1},\ldots ,y_k$
.
Let
![]() $M_r(X;\,{\textbf{y}})$
denote the number of integral solutions
$M_r(X;\,{\textbf{y}})$
denote the number of integral solutions
![]() ${{\textbf{x}}}$
of the system of equations (2·10)
${{\textbf{x}}}$
of the system of equations (2·10)
![]() $(1\leqslant s<t\leqslant r)$
, satisfying
$(1\leqslant s<t\leqslant r)$
, satisfying
![]() $1\leqslant {{\textbf{x}}}\leqslant X$
, wherein
$1\leqslant {{\textbf{x}}}\leqslant X$
, wherein
![]() ${\textbf{y}}=(y_1,\ldots ,y_r)$
is fixed with
${\textbf{y}}=(y_1,\ldots ,y_r)$
is fixed with
![]() $1\leqslant {\textbf{y}}\leqslant X$
and satisfies (2·11). Then it follows from the above discussion in combination with Lemma 2·1 that
$1\leqslant {\textbf{y}}\leqslant X$
and satisfies (2·11). Then it follows from the above discussion in combination with Lemma 2·1 that
in which the maximum is taken over distinct
![]() $y_1,\ldots ,y_r$
with
$y_1,\ldots ,y_r$
with
![]() $1\leqslant {\textbf{y}}\leqslant X$
.
$1\leqslant {\textbf{y}}\leqslant X$
.
Consider fixed values of
![]() $y_1,\ldots ,y_r$
with
$y_1,\ldots ,y_r$
with
![]() $1\leqslant y_i\leqslant X$
$1\leqslant y_i\leqslant X$
![]() $(1\leqslant i\leqslant r)$
. We write
$(1\leqslant i\leqslant r)$
. We write
![]() $N_r(X;\,{\textbf{y}})$
for the number of r-tuples
$N_r(X;\,{\textbf{y}})$
for the number of r-tuples
with
![]() $1\leqslant y_j\leqslant X$
$1\leqslant y_j\leqslant X$
![]() $(r<j\leqslant k)$
. It is apparent from (2·6) and (2·11) that in each such r-tuple, one has
$(r<j\leqslant k)$
. It is apparent from (2·6) and (2·11) that in each such r-tuple, one has
and thus a trivial estimate yields the bound
On the other hand, we may consider the number of d-tuples
with
![]() $1\leqslant y_j\leqslant X$
$1\leqslant y_j\leqslant X$
![]() $(1\leqslant j\leqslant k)$
. Since
$(1\leqslant j\leqslant k)$
. Since
![]() $|{\sigma}_m({\textbf{y}})|\ll X^m$
$|{\sigma}_m({\textbf{y}})|\ll X^m$
![]() $(1\leqslant m\leqslant d)$
, the number of such d-tuples is plainly
$(1\leqslant m\leqslant d)$
, the number of such d-tuples is plainly
![]() $O(X^{d(d+1)/2})$
. Recall that
$O(X^{d(d+1)/2})$
. Recall that
![]() ${\sigma}_0({\textbf{y}})=1$
. Then for each fixed choice of this d-tuple, and for each fixed index j, it follows from (2·6) that the value of
${\sigma}_0({\textbf{y}})=1$
. Then for each fixed choice of this d-tuple, and for each fixed index j, it follows from (2·6) that the value of
![]() $\tau_d(y_1,\ldots,y_k;\,y_j)$
is determined. We therefore infer that
$\tau_d(y_1,\ldots,y_k;\,y_j)$
is determined. We therefore infer that
These simple estimates are already sufficient for many purposes. However, by working harder, one may obtain an estimate that is oftentimes superior to both (3·5) and (3·6). This we establish in Lemma 3·3 below. For the time being we choose not to interrupt our main narrative, and instead explain how bounds for
![]() $N_r(X;\,{\textbf{y}})$
may be applied to estimate
$N_r(X;\,{\textbf{y}})$
may be applied to estimate
![]() $V_{2,r}(X)$
.
$V_{2,r}(X)$
.
When
![]() $1\leqslant j\leqslant r$
, we substitute
$1\leqslant j\leqslant r$
, we substitute
Observe that there are at most
![]() $N_r(X;\,{\textbf{y}})$
distinct values for the integral r-tuple
$N_r(X;\,{\textbf{y}})$
distinct values for the integral r-tuple
![]() $(u_{01},\ldots ,u_{0r})$
. Moreover, in any such r-tuple it follows from (3·4) that
$(u_{01},\ldots ,u_{0r})$
. Moreover, in any such r-tuple it follows from (3·4) that
![]() $1\leqslant |u_{0j}|\ll X^{d(r-1)}$
. There is consequently a positive integer
$1\leqslant |u_{0j}|\ll X^{d(r-1)}$
. There is consequently a positive integer
![]() $C=C(k)$
with the property that, in any solution
$C=C(k)$
with the property that, in any solution
![]() ${{\textbf{x}}},{\textbf{y}}$
counted by
${{\textbf{x}}},{\textbf{y}}$
counted by
![]() $M_r(X;\,{\textbf{y}})$
, one has
$M_r(X;\,{\textbf{y}})$
, one has
![]() $1\leqslant |u_{0j}|\leqslant CX^{d(r-1)}$
.
$1\leqslant |u_{0j}|\leqslant CX^{d(r-1)}$
.
Next we substitute
Then from (2·10) we see that
![]() $M_r(X;\,{\textbf{y}})$
is bounded above by the number of integral solutions of the system
$M_r(X;\,{\textbf{y}})$
is bounded above by the number of integral solutions of the system
 \begin{equation}\prod_{i_1=0}^ku_{i_11}=\prod_{i_2=0}^ku_{i_22}=\ldots =\prod_{i_r=0}^ku_{i_rr},\end{equation}
\begin{equation}\prod_{i_1=0}^ku_{i_11}=\prod_{i_2=0}^ku_{i_22}=\ldots =\prod_{i_r=0}^ku_{i_rr},\end{equation}
with
and with
![]() $u_{0j}$
given by (3·7) for
$u_{0j}$
given by (3·7) for
![]() $1\leqslant j\leqslant r$
. Denote by
$1\leqslant j\leqslant r$
. Denote by
![]() $W(X;\,{\textbf{y}},{{\textbf{u}}}_0)$
the number of integral solutions of the system (3·8) subject to (3·9) and (3·10). Then on recalling (3·2), we may summarise our deliberations thus far concerning
$W(X;\,{\textbf{y}},{{\textbf{u}}}_0)$
the number of integral solutions of the system (3·8) subject to (3·9) and (3·10). Then on recalling (3·2), we may summarise our deliberations thus far concerning
![]() $V_{2,r}(X)$
as follows.
$V_{2,r}(X)$
as follows.
Lemma 3·2. One has
where the maximum with respect to
![]() ${\textbf{y}}=(y_1,\ldots ,y_r)$
is taken over
${\textbf{y}}=(y_1,\ldots ,y_r)$
is taken over
![]() $y_1,\ldots ,y_r$
distinct with
$y_1,\ldots ,y_r$
distinct with
![]() $1\leqslant y_j\leqslant X$
$1\leqslant y_j\leqslant X$
![]() $(1\leqslant j\leqslant r)$
, and the maximum over r-tuples
$(1\leqslant j\leqslant r)$
, and the maximum over r-tuples
![]() ${{\textbf{u}}}_0=(u_{01},\ldots ,u_{0r})$
is taken over
${{\textbf{u}}}_0=(u_{01},\ldots ,u_{0r})$
is taken over
Before fulfilling our commitment to establish an estimate for
![]() $N_r(X;\,{\textbf{y}})$
sharper than the pedestrian bounds already obtained, we introduce the exponent
$N_r(X;\,{\textbf{y}})$
sharper than the pedestrian bounds already obtained, we introduce the exponent
Lemma 3·3.
Let d and r be non-negative integers and let
![]() $C\geqslant 1$
be fixed. Also, let
$C\geqslant 1$
be fixed. Also, let
Finally, when
![]() ${\textbf{a}}\in {\mathcal A}_d$
, define
${\textbf{a}}\in {\mathcal A}_d$
, define
Suppose that
![]() $y_1,\ldots ,y_r$
are fixed integers with
$y_1,\ldots ,y_r$
are fixed integers with
![]() $1\leqslant y_i\leqslant X$
$1\leqslant y_i\leqslant X$
![]() $(1\leqslant i\leqslant r)$
. Then one has
$(1\leqslant i\leqslant r)$
. Then one has
Proof. We proceed by induction on d. Note first that when
![]() $d=0$
, the polynomials
$d=0$
, the polynomials
![]() $f_{\textbf{a}}(t)$
are necessarily constant with
$f_{\textbf{a}}(t)$
are necessarily constant with
![]() $|a_0|\leqslant C$
, and thus
$|a_0|\leqslant C$
, and thus
Since
![]() ${\theta}_{0,r}=0$
, the conclusion of the lemma follows for
${\theta}_{0,r}=0$
, the conclusion of the lemma follows for
![]() $d=0$
. Observe also that when
$d=0$
. Observe also that when
![]() $r=0$
the conclusion of the lemma is trivial, for then one has
$r=0$
the conclusion of the lemma is trivial, for then one has
![]() ${\theta}_{d,0}=0$
and the set of values in question is empty.
${\theta}_{d,0}=0$
and the set of values in question is empty.
Having established the base of the induction, we proceed under the assumption that the conclusion of the lemma holds whenever
![]() $d<D$
, for some integer D with
$d<D$
, for some integer D with
![]() $D\geqslant 1$
. In view of the discussion of the previous paragraph, we may now restrict attention to the situation with
$D\geqslant 1$
. In view of the discussion of the previous paragraph, we may now restrict attention to the situation with
![]() $d=D\geqslant 1$
and
$d=D\geqslant 1$
and
![]() $r\geqslant 1$
. Since
$r\geqslant 1$
. Since
![]() $1\leqslant y_r\leqslant X$
and
$1\leqslant y_r\leqslant X$
and
![]() $y_r$
is fixed, we see that whenever
$y_r$
is fixed, we see that whenever
![]() ${\textbf{a}}\in {\mathcal A}_D$
one has
${\textbf{a}}\in {\mathcal A}_D$
one has
Put
so that
 \begin{align*}g_{\textbf{a}}(y_r,t)=\sum_{l=1}^Da_l\!\left(t^{l-1}+t^{l-2}y_r+\ldots +y_r^{l-1}\right).\end{align*}
\begin{align*}g_{\textbf{a}}(y_r,t)=\sum_{l=1}^Da_l\!\left(t^{l-1}+t^{l-2}y_r+\ldots +y_r^{l-1}\right).\end{align*}
Then one sees that whenever
![]() ${\textbf{a}}\in {\mathcal A}_D$
, one may write
${\textbf{a}}\in {\mathcal A}_D$
, one may write
where
and, for
![]() $0\leqslant l\leqslant D-1$
, one has
$0\leqslant l\leqslant D-1$
, one has
Put
Then the inductive hypothesis for
![]() $d=D-1$
implies that
$d=D-1$
implies that
On recalling (3·13) and (3·14), we see that
The values of
![]() $y_i$
$y_i$
![]() $(1\leqslant i\leqslant r-1)$
are fixed, and by (3·15) there are
$(1\leqslant i\leqslant r-1)$
are fixed, and by (3·15) there are
![]() $O(X^{{\theta}_{D-1,r-1}})$
possible choices for
$O(X^{{\theta}_{D-1,r-1}})$
possible choices for
![]() $F_{{\textbf{b}}}(y_i)$
$F_{{\textbf{b}}}(y_i)$
![]() $(1\leqslant i\leqslant r-1)$
. Then for each fixed choice of
$(1\leqslant i\leqslant r-1)$
. Then for each fixed choice of
![]() $f_{\textbf{a}}(y_r)$
, there are
$f_{\textbf{a}}(y_r)$
, there are
![]() $O(X^{{\theta}_{D-1,r-1}})$
choices available for
$O(X^{{\theta}_{D-1,r-1}})$
choices available for
![]() $f_{\textbf{a}}(y_i)$
$f_{\textbf{a}}(y_i)$
![]() $(1\leqslant i\leqslant r-1)$
. We therefore deduce from (3·12) that
$(1\leqslant i\leqslant r-1)$
. We therefore deduce from (3·12) that
Since, from (3·11), one has
 \begin{align*}{\theta}_{D-1,r-1}+D&=D+\sum_{l=1}^{r-1}\max \{ (D-1)-l+1,0\}\\&=\sum_{l=1}^r\max \{ D-l+1,0\}={\theta}_{D,r},\end{align*}
\begin{align*}{\theta}_{D-1,r-1}+D&=D+\sum_{l=1}^{r-1}\max \{ (D-1)-l+1,0\}\\&=\sum_{l=1}^r\max \{ D-l+1,0\}={\theta}_{D,r},\end{align*}
we find that
The inductive hypothesis therefore follows for
![]() $d=D$
and all values of r. The conclusion of the lemma consequently follows by induction.
$d=D$
and all values of r. The conclusion of the lemma consequently follows by induction.
On recalling (2·6), a brief perusal of (3·3) and the definition of
![]() $N_r(X;\,{\textbf{y}})$
leads from Lemma 3·3 to the estimate
$N_r(X;\,{\textbf{y}})$
leads from Lemma 3·3 to the estimate
![]() $N_r(X;\,{\textbf{y}})\ll X^{{\theta}_{d,r}}$
. We may therefore conclude this section with the following upper bound for
$N_r(X;\,{\textbf{y}})\ll X^{{\theta}_{d,r}}$
. We may therefore conclude this section with the following upper bound for
![]() $I_{k,d}(X)-T_k(X)$
.
$I_{k,d}(X)-T_k(X)$
.
Lemma 3·4. One has
where the maximum is taken over distinct
![]() $y_1,\ldots ,y_r$
with
$y_1,\ldots ,y_r$
with
![]() $1\leqslant y_j\leqslant X$
and over
$1\leqslant y_j\leqslant X$
and over
![]() $1\leqslant |u_{0j}|\leqslant CX^{d(r-1)}$
$1\leqslant |u_{0j}|\leqslant CX^{d(r-1)}$
![]() $(1\leqslant j\leqslant r)$
.
$(1\leqslant j\leqslant r)$
.
Proof. It follows from Lemma 3·2 together with the bound for
![]() $N_r(X;\,{\textbf{y}})$
just obtained that
$N_r(X;\,{\textbf{y}})$
just obtained that
The conclusion of the lemma is obtained by substituting this estimate together with that supplied by Lemma 3·1 into (3·1).
4. Exploiting multiplicative relations
Our goal in this section is to estimate the quantity
![]() $W(X;\,{\textbf{y}},{{\textbf{u}}}_0)$
that counts solutions of the multiplicative equations (3·8) equipped with their ancillary conditions (3·9) and (3·10). For this purpose, we follow closely the trail first adopted in our work with Vaughan [
Reference Vaughan and Wooley10
, Section 2].
$W(X;\,{\textbf{y}},{{\textbf{u}}}_0)$
that counts solutions of the multiplicative equations (3·8) equipped with their ancillary conditions (3·9) and (3·10). For this purpose, we follow closely the trail first adopted in our work with Vaughan [
Reference Vaughan and Wooley10
, Section 2].
Lemma 4·1.
Suppose that
![]() $y_1,\ldots ,y_r$
are distinct integers with
$y_1,\ldots ,y_r$
are distinct integers with
![]() $1\leqslant {\textbf{y}}\leqslant X$
, and that
$1\leqslant {\textbf{y}}\leqslant X$
, and that
![]() $u_{0j}$
$u_{0j}$
![]() $(1\leqslant j\leqslant r)$
are integers with
$(1\leqslant j\leqslant r)$
are integers with
![]() $1\leqslant |u_{0j}|\leqslant CX^{d(r-1)}$
. Then one has
$1\leqslant |u_{0j}|\leqslant CX^{d(r-1)}$
. Then one has
![]() $W(X;\,{\textbf{y}},{{\textbf{u}}}_0)\ll X^{k/r+\varepsilon}$
.
$W(X;\,{\textbf{y}},{{\textbf{u}}}_0)\ll X^{k/r+\varepsilon}$
.
Proof. We begin with a notational device from [
Reference Vaughan and Wooley10
, section 2]. Let
![]() ${\mathcal I}$
denote the set of indices
${\mathcal I}$
denote the set of indices
![]() ${{\textbf{i}}}=(i_1,\ldots ,i_r)$
with
${{\textbf{i}}}=(i_1,\ldots ,i_r)$
with
![]() $0\leqslant i_m\leqslant k$
$0\leqslant i_m\leqslant k$
![]() $(1\leqslant m\leqslant r)$
. Define the map
$(1\leqslant m\leqslant r)$
. Define the map
![]() $\varphi\,:\,{\mathcal I} \rightarrow [0,(k+1)^r)\cap {\mathbb Z}$
by putting
$\varphi\,:\,{\mathcal I} \rightarrow [0,(k+1)^r)\cap {\mathbb Z}$
by putting
The map
![]() $\varphi$
is bijective, and we may define the successor
$\varphi$
is bijective, and we may define the successor
![]() ${{\textbf{i}}}+1$
of the index
${{\textbf{i}}}+1$
of the index
![]() ${{\textbf{i}}}$
by means of the relation
${{\textbf{i}}}$
by means of the relation
We then define
![]() ${{\textbf{i}}}+h$
inductively via the formula
${{\textbf{i}}}+h$
inductively via the formula
![]() ${{\textbf{i}}}+(h+1)=({{\textbf{i}}}+h)+1$
. Finally, when
${{\textbf{i}}}+(h+1)=({{\textbf{i}}}+h)+1$
. Finally, when
![]() ${{\textbf{i}}}\in {\mathcal I}$
, we write
${{\textbf{i}}}\in {\mathcal I}$
, we write
![]() ${\mathcal J}({{\textbf{i}}})$
for the set of indices
${\mathcal J}({{\textbf{i}}})$
for the set of indices
![]() ${{\textbf{j}}}\in {\mathcal I}$
having the property that, for some
${{\textbf{j}}}\in {\mathcal I}$
having the property that, for some
![]() $h\in {\mathbb N}$
, one has
$h\in {\mathbb N}$
, one has
![]() ${{\textbf{j}}}+h={{\textbf{i}}}$
. Thus, the set
${{\textbf{j}}}+h={{\textbf{i}}}$
. Thus, the set
![]() ${\mathcal J}({{\textbf{i}}})$
is the set of all precursors of
${\mathcal J}({{\textbf{i}}})$
is the set of all precursors of
![]() ${{\textbf{i}}}$
, in the natural sense.
${{\textbf{i}}}$
, in the natural sense.
Equipped with this notation, we now explain how systematically to extract common factors between the variables in the system of equations (3·8). Put
noting that by hypothesis, this integer is fixed. Suppose at stage
![]() ${{\textbf{i}}}$
that
${{\textbf{i}}}$
that
![]() ${\alpha}_{{\textbf{j}}}$
has been defined for all
${\alpha}_{{\textbf{j}}}$
has been defined for all
![]() ${{\textbf{j}}}\in {\mathcal J}({{\textbf{i}}})$
. We then define
${{\textbf{j}}}\in {\mathcal J}({{\textbf{i}}})$
. We then define
 \begin{align*}{\alpha}_{{\textbf{i}}}=\left( \frac{u_{i_11}}{{\beta}^{(1)}_{{\textbf{i}}}},\frac{u_{i_22}}{{\beta}^{(2)}_{{\textbf{i}}}},\ldots,\frac{u_{i_rr}}{{\beta}^{(r)}_{{\textbf{i}}}}\right) ,\end{align*}
\begin{align*}{\alpha}_{{\textbf{i}}}=\left( \frac{u_{i_11}}{{\beta}^{(1)}_{{\textbf{i}}}},\frac{u_{i_22}}{{\beta}^{(2)}_{{\textbf{i}}}},\ldots,\frac{u_{i_rr}}{{\beta}^{(r)}_{{\textbf{i}}}}\right) ,\end{align*}
in which we write
 \begin{align*}{\beta}^{(m)}_{{\textbf{i}}}=\prod_{\substack{{{\textbf{j}}}\in {\mathcal J}({{\textbf{i}}})\\ j_m=i_m}}{\alpha}_{{\textbf{j}}} .\end{align*}
\begin{align*}{\beta}^{(m)}_{{\textbf{i}}}=\prod_{\substack{{{\textbf{j}}}\in {\mathcal J}({{\textbf{i}}})\\ j_m=i_m}}{\alpha}_{{\textbf{j}}} .\end{align*}
As is usual, the empty product is interpreted to be 1. As a means of preserving intuition concerning the numerous variables generated in this way, we write
 \begin{align*}{\widetilde \alpha}_{lm}^\pm=\pm\prod_{\substack{{{\textbf{j}}}\in {\mathcal I}\\ j_m=l}}{\alpha}_{{\textbf{j}}}\quad(0\leqslant l\leqslant k,\, 1\leqslant m\leqslant r).\end{align*}
\begin{align*}{\widetilde \alpha}_{lm}^\pm=\pm\prod_{\substack{{{\textbf{j}}}\in {\mathcal I}\\ j_m=l}}{\alpha}_{{\textbf{j}}}\quad(0\leqslant l\leqslant k,\, 1\leqslant m\leqslant r).\end{align*}
Then, much as in [
Reference Vaughan and Wooley10
, section 2], it follows that when
![]() $0\leqslant l\leqslant k$
and
$0\leqslant l\leqslant k$
and
![]() $1\leqslant m\leqslant r$
, for some choice of the sign
$1\leqslant m\leqslant r$
, for some choice of the sign
![]() $\pm$
, one has
$\pm$
, one has
![]() $u_{lm}={\widetilde \alpha}_{lm}^\pm$
. Note here that the ambiguity in the sign of
$u_{lm}={\widetilde \alpha}_{lm}^\pm$
. Note here that the ambiguity in the sign of
![]() $u_{lm}$
relative to
$u_{lm}$
relative to
![]() $|{\widetilde \alpha}_{lm}^\pm|$
is a feature overlooked in the treatment of [
Reference Vaughan and Wooley10
], though the ensuing argument requires no significant modification to be brought to play in order that the same conclusion be obtained. At worst, an additional factor
$|{\widetilde \alpha}_{lm}^\pm|$
is a feature overlooked in the treatment of [
Reference Vaughan and Wooley10
], though the ensuing argument requires no significant modification to be brought to play in order that the same conclusion be obtained. At worst, an additional factor
![]() $2^{r(k+1)}$
would need to be absorbed into the constants implicit in Vinogradov’s notation.
$2^{r(k+1)}$
would need to be absorbed into the constants implicit in Vinogradov’s notation.
With this notation in hand, it follows from its definition that
![]() $W(X;\,{\textbf{y}},{{\textbf{u}}}_0)$
is bounded above by the number
$W(X;\,{\textbf{y}},{{\textbf{u}}}_0)$
is bounded above by the number
![]() ${\Omega}_r(X;\,{\textbf{y}},{{\textbf{u}}}_0)$
of solutions of the system
${\Omega}_r(X;\,{\textbf{y}},{{\textbf{u}}}_0)$
of solutions of the system
with
Notice here that
![]() ${\widetilde \alpha}^\pm_{0m}=u_{0m}$
. Thus, it follows from a divisor function estimate that when the integers
${\widetilde \alpha}^\pm_{0m}=u_{0m}$
. Thus, it follows from a divisor function estimate that when the integers
![]() $u_{0m}$
are fixed with
$u_{0m}$
are fixed with
then there are
![]() $O(X^\varepsilon)$
possible choices for the variables
$O(X^\varepsilon)$
possible choices for the variables
![]() ${\alpha}_{{\textbf{i}}}$
having the property that
${\alpha}_{{\textbf{i}}}$
having the property that
![]() $i_m=0$
for some index m with
$i_m=0$
for some index m with
![]() $1\leqslant m\leqslant r$
.
$1\leqslant m\leqslant r$
.
Having carefully prepared the notational infrastructure to make comparison with [
Reference Vaughan and Wooley10
, sections 2 and 3] transparent, we may now follow the argument of the latter mutatis mutandis. When
![]() $1\leqslant p\leqslant r$
, we write
$1\leqslant p\leqslant r$
, we write
where the product is taken over all
![]() ${{\textbf{i}}}\in {\mathcal I}$
with
${{\textbf{i}}}\in {\mathcal I}$
with
![]() $i_l>i_p$
$i_l>i_p$
![]() $(l\ne p)$
, and
$(l\ne p)$
, and
![]() $i_l>0$
$i_l>0$
![]() $(1\leqslant l\leqslant r)$
. Thus, in view of (4·2), one has
$(1\leqslant l\leqslant r)$
. Thus, in view of (4·2), one has
 \begin{align*}\prod_{p=1}^rB_p\leqslant \prod_{\substack{{{\textbf{i}}}\in {\mathcal I}\\ i_l>0\, (1\leqslant l\leqslant r)}}{\alpha}_{{\textbf{i}}} \leqslant \prod_{i=1}^k|{\widetilde \alpha}^\pm_{i1}|\leqslant X^k,\end{align*}
\begin{align*}\prod_{p=1}^rB_p\leqslant \prod_{\substack{{{\textbf{i}}}\in {\mathcal I}\\ i_l>0\, (1\leqslant l\leqslant r)}}{\alpha}_{{\textbf{i}}} \leqslant \prod_{i=1}^k|{\widetilde \alpha}^\pm_{i1}|\leqslant X^k,\end{align*}
and so in any solution
![]() ${\boldsymbol \alpha}^\pm$
of (4·1) counted by
${\boldsymbol \alpha}^\pm$
of (4·1) counted by
![]() ${\Omega}_r(X;\,{\textbf{y}},{{\textbf{u}}}_0)$
, there exists an index p with
${\Omega}_r(X;\,{\textbf{y}},{{\textbf{u}}}_0)$
, there exists an index p with
![]() $1\leqslant p\leqslant r$
such that
$1\leqslant p\leqslant r$
such that
By relabelling variables, we consequently deduce that
where
![]() ${\Upsilon}_r(X;\,{\textbf{y}},{{\textbf{u}}}_0)$
denotes the number of integral solutions of the system
${\Upsilon}_r(X;\,{\textbf{y}},{{\textbf{u}}}_0)$
denotes the number of integral solutions of the system
with
![]() $L_j=y_j-y_1$
$L_j=y_j-y_1$
![]() $(2\leqslant j\leqslant r)$
, and with the integral tuples
$(2\leqslant j\leqslant r)$
, and with the integral tuples
![]() ${\alpha}_{{\textbf{i}}}$
satisfying (4·2) together with the inequality
${\alpha}_{{\textbf{i}}}$
satisfying (4·2) together with the inequality
We emphasise here that, when
![]() $y_1,\ldots ,y_r$
are distinct, then
$y_1,\ldots ,y_r$
are distinct, then
![]() $L_j\ne 0$
$L_j\ne 0$
![]() $(2\leqslant j\leqslant r)$
.
$(2\leqslant j\leqslant r)$
.
We now proceed under the assumption that
![]() $y_1,\ldots ,y_r$
are fixed and distinct, whence the integers
$y_1,\ldots ,y_r$
are fixed and distinct, whence the integers
![]() $L_j$
$L_j$
![]() $(2\leqslant j\leqslant r)$
are fixed and non-zero. It follows just as in the final paragraphs of [
Reference Vaughan and Wooley10
, section 2] that, when the variables
$(2\leqslant j\leqslant r)$
are fixed and non-zero. It follows just as in the final paragraphs of [
Reference Vaughan and Wooley10
, section 2] that, when the variables
![]() ${\alpha}_{{\textbf{i}}}$
, with
${\alpha}_{{\textbf{i}}}$
, with
![]() ${{\textbf{i}}}\in {\mathcal I}$
satisfying
${{\textbf{i}}}\in {\mathcal I}$
satisfying
![]() $i_l>i_1$
$i_l>i_1$
![]() $(2\leqslant l\leqslant r)$
, are fixed, then there are
$(2\leqslant l\leqslant r)$
, are fixed, then there are
![]() $O(X^\varepsilon)$
possible choices for the tuples
$O(X^\varepsilon)$
possible choices for the tuples
![]() ${\alpha}_{{\textbf{i}}}$
satisfying (4·2) and (4·5). Here we make use of the fact that the variables
${\alpha}_{{\textbf{i}}}$
satisfying (4·2) and (4·5). Here we make use of the fact that the variables
![]() ${\alpha}_{{\textbf{i}}}$
, in which
${\alpha}_{{\textbf{i}}}$
, in which
![]() $i_m=0$
for some index m with
$i_m=0$
for some index m with
![]() $1\leqslant m\leqslant r$
, may be considered fixed with the potential loss of a factor
$1\leqslant m\leqslant r$
, may be considered fixed with the potential loss of a factor
![]() $O(X^\varepsilon)$
in the resulting estimates. By making use of standard estimates for the divisor function, however, we find from (4·6) and the definition (4·3) that there are
$O(X^\varepsilon)$
in the resulting estimates. By making use of standard estimates for the divisor function, however, we find from (4·6) and the definition (4·3) that there are
![]() $O(X^{k/r+\varepsilon})$
possible choices for the variables
$O(X^{k/r+\varepsilon})$
possible choices for the variables
![]() ${\alpha}_{{\textbf{i}}}$
with
${\alpha}_{{\textbf{i}}}$
with
![]() ${{\textbf{i}}}\in {\mathcal I}$
satisfying
${{\textbf{i}}}\in {\mathcal I}$
satisfying
![]() $i_l>i_1$
$i_l>i_1$
![]() $(2\leqslant l\leqslant r)$
. We therefore infer that
$(2\leqslant l\leqslant r)$
. We therefore infer that
![]() ${\Upsilon}_r(X;\,{\textbf{y}},{{\textbf{u}}}_0)\ll X^{k/r+\varepsilon}$
, whence
${\Upsilon}_r(X;\,{\textbf{y}},{{\textbf{u}}}_0)\ll X^{k/r+\varepsilon}$
, whence
![]() ${\Omega}_r(X;\,{\textbf{y}},{{\textbf{u}}}_0)\ll X^{k/r+\varepsilon}$
, and finally
${\Omega}_r(X;\,{\textbf{y}},{{\textbf{u}}}_0)\ll X^{k/r+\varepsilon}$
, and finally
![]() $W(X;\,{\textbf{y}},{{\textbf{u}}}_0)\ll X^{k/r+\varepsilon}$
. This completes the proof of the lemma.
$W(X;\,{\textbf{y}},{{\textbf{u}}}_0)\ll X^{k/r+\varepsilon}$
. This completes the proof of the lemma.
The proof of Theorem 1·1 is now at hand. By applying Lemma 3·4 in combination with Lemma 4·1, we obtain the upper bound
By minimising the right-hand side over
![]() $2\leqslant r\leqslant k$
, a comparison of (1·6) and (3·11) now confirms that this estimate delivers the one claimed in the statement of Theorem 1·1.
$2\leqslant r\leqslant k$
, a comparison of (1·6) and (3·11) now confirms that this estimate delivers the one claimed in the statement of Theorem 1·1.
5. Corollaries and refinements
We complete our discussion of incomplete Vinogradov systems by first deriving the corollaries to Theorem 1·1 presented in the introduction, and then considering refinements to the main strategy.
The proof of Corollary 1·2. Suppose that
![]() $d\leqslant \sqrt{k}$
and take r to be the integer closest to
$d\leqslant \sqrt{k}$
and take r to be the integer closest to
![]() $\sqrt{k}$
. Thus
$\sqrt{k}$
. Thus
![]() $d\leqslant r$
and we find from (1·6) that
$d\leqslant r$
and we find from (1·6) that
An application of Theorem 1·1 therefore leads us to the asymptotic formula
confirming the first claim of the corollary. In particular, when
![]() $d=o\!\left(k^{1/4}\right)$
, we discern that
$d=o\!\left(k^{1/4}\right)$
, we discern that
and so the final claim of the corollary follows.
The proof of Corollary 1·3. Suppose that
![]() $d\geqslant 1$
and
$d\geqslant 1$
and
![]() $k\geqslant 4d+3$
. In this situation, by reference to (1·6) with
$k\geqslant 4d+3$
. In this situation, by reference to (1·6) with
![]() $r=2$
, we find that
$r=2$
, we find that
Consequently, it follows from Theorem 1·1 that
![]() $I_{k,d}(X)-T_k(X)\ll X^{k-1/2}$
, so that the first claim of the corollary follows.
$I_{k,d}(X)-T_k(X)\ll X^{k-1/2}$
, so that the first claim of the corollary follows.
Next by considering (1·6) with r taken to be the integer closest to
![]() $\sqrt{k/(d+1)}$
, we find that
$\sqrt{k/(d+1)}$
, we find that
In this instance, Theorem 1·1 supplies the asymptotic formula
which establishes the second claim of the corollary.
Finally, when
![]() $\eta$
is small and positive, and
$\eta$
is small and positive, and
![]() $1\leqslant d\leqslant \eta^2 k$
, one finds that
$1\leqslant d\leqslant \eta^2 k$
, one finds that
The final estimate of the corollary follows, and this completes the proof.
Some refinement is possible within the argument applied in the proof of Theorem 1·1 for smaller values of k. Thus, an argument analogous to that discussed in the final paragraph of [
Reference Vaughan and Wooley10
, section 2] shows that the bound
![]() $1\leqslant B_p\leqslant X^{k/r}$
of equation (4·4) may be replaced by the corresponding bound
$1\leqslant B_p\leqslant X^{k/r}$
of equation (4·4) may be replaced by the corresponding bound
where we write
 \begin{align*}{\omega}(k,r)=k^{1-r}\sum_{i=1}^{k-1}i^{r-1}.\end{align*}
\begin{align*}{\omega}(k,r)=k^{1-r}\sum_{i=1}^{k-1}i^{r-1}.\end{align*}
In order to justify this assertion, denote by
![]() ${\mathcal I}^+$
the set of indices
${\mathcal I}^+$
the set of indices
![]() ${{\textbf{i}}}\in {\mathcal I}$
such that
${{\textbf{i}}}\in {\mathcal I}$
such that
![]() $i_l>0$
$i_l>0$
![]() $(1\leqslant l\leqslant r)$
, and let
$(1\leqslant l\leqslant r)$
, and let
![]() ${\mathcal I}^*$
denote the corresponding set of indices subject to the additional condition that for some index p with
${\mathcal I}^*$
denote the corresponding set of indices subject to the additional condition that for some index p with
![]() $1\leqslant p\leqslant r$
, one has
$1\leqslant p\leqslant r$
, one has
![]() $i_l>i_p$
whenever
$i_l>i_p$
whenever
![]() $l\ne p$
. Then, just as in [
Reference Vaughan and Wooley10
, section 2], one has
$l\ne p$
. Then, just as in [
Reference Vaughan and Wooley10
, section 2], one has
![]() $\text{card}({\mathcal I}^+)=k^r$
and
$\text{card}({\mathcal I}^+)=k^r$
and
![]() $\text{card}({\mathcal I}^*)=r\psi_r(k)$
, where
$\text{card}({\mathcal I}^*)=r\psi_r(k)$
, where
 \begin{align*}\psi_r(k)=\sum_{i=1}^{k-1}i^{r-1}<k^r/r.\end{align*}
\begin{align*}\psi_r(k)=\sum_{i=1}^{k-1}i^{r-1}<k^r/r.\end{align*}
In the situation of the proof of Lemma 4·1 in section 4, the variables
![]() ${\alpha}_{{\textbf{i}}}$
with
${\alpha}_{{\textbf{i}}}$
with
![]() $i_l=0$
for some index l with
$i_l=0$
for some index l with
![]() $1\leqslant l\leqslant r$
are already determined via a divisor function estimate. By permuting and relabelling indices
$1\leqslant l\leqslant r$
are already determined via a divisor function estimate. By permuting and relabelling indices
![]() $i_l$
, for each fixed index l, as necessary, the argument of the proof can be adapted to show that
$i_l$
, for each fixed index l, as necessary, the argument of the proof can be adapted to show that
![]() $W(X;\,{\textbf{y}},{{\textbf{u}}}_0)\ll Y_r(X)$
, where
$W(X;\,{\textbf{y}},{{\textbf{u}}}_0)\ll Y_r(X)$
, where
![]() $Y_r(X)$
denotes the number of solutions
$Y_r(X)$
denotes the number of solutions
![]() ${\boldsymbol \alpha}^\pm$
as before, but subject to the additional condition
${\boldsymbol \alpha}^\pm$
as before, but subject to the additional condition
 \begin{align*}\prod_{{{\textbf{i}}}\in {\mathcal I}^*}{\alpha}_{{\textbf{i}}} \leqslant \Biggl( \prod_{{{\textbf{i}}}\in {\mathcal I}^+}{\alpha}_{{\textbf{i}}} \Biggr)^{\text{card}({\mathcal I}^*)/\text{card}({\mathcal I}^+)}.\end{align*}
\begin{align*}\prod_{{{\textbf{i}}}\in {\mathcal I}^*}{\alpha}_{{\textbf{i}}} \leqslant \Biggl( \prod_{{{\textbf{i}}}\in {\mathcal I}^+}{\alpha}_{{\textbf{i}}} \Biggr)^{\text{card}({\mathcal I}^*)/\text{card}({\mathcal I}^+)}.\end{align*}
Then
 \begin{align*}\prod_{p=1}^rB_p\leqslant \prod_{{{\textbf{i}}}\in {\mathcal I}^*}{\alpha}_{{\textbf{i}}} \leqslant (X^k)^{r\psi_r(k)/k^r}.\end{align*}
\begin{align*}\prod_{p=1}^rB_p\leqslant \prod_{{{\textbf{i}}}\in {\mathcal I}^*}{\alpha}_{{\textbf{i}}} \leqslant (X^k)^{r\psi_r(k)/k^r}.\end{align*}
Consequently, in any solution
![]() ${\boldsymbol \alpha}^\pm$
of (4·1) counted by
${\boldsymbol \alpha}^\pm$
of (4·1) counted by
![]() ${\Omega}_r(X;\,{\textbf{y}};\,{{\textbf{u}}}_0)$
, there exists an index p with
${\Omega}_r(X;\,{\textbf{y}};\,{{\textbf{u}}}_0)$
, there exists an index p with
![]() $1\leqslant p\leqslant r$
such that
$1\leqslant p\leqslant r$
such that
By pursuing the same argument as in our earlier treatment, mutatis mutandis, we now derive the upper bound
where
 \begin{align*}{\gamma}^\prime_{k,d}=\min_{2\leqslant r\leqslant k}\left( r+{\omega}(k,r)+\sum_{l=1}^r\max\{ d-l+1,0\}\right).\end{align*}
\begin{align*}{\gamma}^\prime_{k,d}=\min_{2\leqslant r\leqslant k}\left( r+{\omega}(k,r)+\sum_{l=1}^r\max\{ d-l+1,0\}\right).\end{align*}
We conclude from these deliberations that Theorem 1·1 and the first conclusion of Corollary 1·3 may be refined as follows.
Theorem 5·1.
Suppose that
![]() $k\geqslant 3$
and
$k\geqslant 3$
and
![]() $0\leqslant d<k/2$
. Then, for each
$0\leqslant d<k/2$
. Then, for each
![]() $\varepsilon>0$
, one has
$\varepsilon>0$
, one has
where
 \begin{align*}{\gamma}^\prime_{k,d}=\min_{2\leqslant r\leqslant k}\left( r+k^{1-r}\sum_{i=1}^{k-1}i^{r-1}+\sum_{l=1}^r\max\{ d-l+1,0\}\right) .\end{align*}
\begin{align*}{\gamma}^\prime_{k,d}=\min_{2\leqslant r\leqslant k}\left( r+k^{1-r}\sum_{i=1}^{k-1}i^{r-1}+\sum_{l=1}^r\max\{ d-l+1,0\}\right) .\end{align*}
In particular, provided that
![]() $d\geqslant 1$
and
$d\geqslant 1$
and
![]() $k\geqslant 4d+2$
, one has
$k\geqslant 4d+2$
, one has
Proof. The proof of the first conclusion has already been outlined. As for the second, by taking
![]() $r=2$
we discern that
$r=2$
we discern that
Thus, provided that
![]() $k>4d+1$
, one finds that
$k>4d+1$
, one finds that
![]() ${\gamma}^\prime_{k,d}\leqslant k-1/2$
, and hence the final conclusion of the theorem follows from the first.
${\gamma}^\prime_{k,d}\leqslant k-1/2$
, and hence the final conclusion of the theorem follows from the first.
Energetic readers will find a smorgasbord of problems to investigate allied to those examined in this paper. We mention three in order to encourage work on these topics.
We begin by noting that the conclusions of Theorem 1·1 establish the paucity of non-diagonal solutions in the system (1·5) when d is smaller than about
![]() $k/4$
. In principle, the methods employed remain useful when
$k/4$
. In principle, the methods employed remain useful when
![]() $d<k/2$
. However, when
$d<k/2$
. However, when
![]() $d>k/2$
the analogue of the identity (2·4) that would be obtained would contain terms involving
$d>k/2$
the analogue of the identity (2·4) that would be obtained would contain terms involving
![]() $h^2$
, or even larger powers of h, and this precludes the possibility of eliminating all of the terms involving h in any useful manner. A simple test case would be the situation with
$h^2$
, or even larger powers of h, and this precludes the possibility of eliminating all of the terms involving h in any useful manner. A simple test case would be the situation with
![]() $d=k-1$
, wherein the system (1·5) assumes the shape
$d=k-1$
, wherein the system (1·5) assumes the shape
When
![]() $k=3$
an affine slicing approach has been employed in [
Reference Wooley12
] to resolve the associated paucity problem. It would be interesting to address this problem when
$k=3$
an affine slicing approach has been employed in [
Reference Wooley12
] to resolve the associated paucity problem. It would be interesting to address this problem when
![]() $k\geqslant 4$
.
$k\geqslant 4$
.
The focus of this paper has been on the situation in which one slice is removed from a Vinogradov system. When more than one slice is removed, two or more auxiliary variables
![]() $h_1,h_2,\ldots $
take the place of the single variable h in the identity (2·4), and this seems to pose serious problems for our methods. A simple test case in this context would address the system of equations
$h_1,h_2,\ldots $
take the place of the single variable h in the identity (2·4), and this seems to pose serious problems for our methods. A simple test case in this context would address the system of equations
with
![]() $k\geqslant 3$
. Here, the situation with
$k\geqslant 3$
. Here, the situation with
![]() $k=3$
has been successfully addressed by a number of authors (see [
Reference Greaves3
,
Reference Skinner and Wooley8
] and [
Reference Salberger6
, corollary 0·3]), but little seems to be known for
$k=3$
has been successfully addressed by a number of authors (see [
Reference Greaves3
,
Reference Skinner and Wooley8
] and [
Reference Salberger6
, corollary 0·3]), but little seems to be known for
![]() $k\geqslant 4$
. Much more is known when the omitted slices are carefully chosen so that the resulting systems assume a special shape. Most obviously, one could consider systems of the shape
$k\geqslant 4$
. Much more is known when the omitted slices are carefully chosen so that the resulting systems assume a special shape. Most obviously, one could consider systems of the shape
By specialising variables, one finds from [
Reference Vaughan and Wooley10
, theorem 1] that the number of non-diagonal solutions of this system with
![]() $1\leqslant {{\textbf{x}}},{\textbf{y}}\leqslant X$
is
$1\leqslant {{\textbf{x}}},{\textbf{y}}\leqslant X$
is
![]() $O(X^{t\sqrt{4k+1}})$
, and this is
$O(X^{t\sqrt{4k+1}})$
, and this is
![]() $o(T_k(X))$
provided only that the integer t is smaller than
$o(T_k(X))$
provided only that the integer t is smaller than
![]() $\tfrac{1}{2}\sqrt{k}-1$
. Moreover, the ingenious work of Brüdern and Robert [
Reference Brüdern and Robert2
] shows that when
$\tfrac{1}{2}\sqrt{k}-1$
. Moreover, the ingenious work of Brüdern and Robert [
Reference Brüdern and Robert2
] shows that when
![]() $k\geqslant 4$
, there is a paucity of non-diagonal solutions to systems of the shape
$k\geqslant 4$
, there is a paucity of non-diagonal solutions to systems of the shape
wherein all of the even degree slices are omitted. A strategy for systems having arbitrary exponents can be extracted from [
Reference Wooley11
], though the work there misses a paucity estimate by a factor
![]() $(\log X)^A$
, for a suitable
$(\log X)^A$
, for a suitable
![]() $A>0$
.
$A>0$
.
We remark finally that the system of equations (1·5) central to Theorem 1·1 has the property that there are
![]() $k-1$
equations and k pairs of variables
$k-1$
equations and k pairs of variables
![]() $x_i,y_i$
. No paucity result is available when the number of pairs of variables exceeds k. The simplest challenge in this direction would be to establish that when
$x_i,y_i$
. No paucity result is available when the number of pairs of variables exceeds k. The simplest challenge in this direction would be to establish that when
![]() $k\geqslant 3$
, one has
$k\geqslant 3$
, one has
Acknowledgements
The author’s work is supported by NSF grant DMS-2001549 and the Focused Research Group grant DMS-1854398. The author is grateful to the referee of this paper for their time and attention.