Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T20:42:03.439Z Has data issue: false hasContentIssue false
  • English
  • Français

Overstable convection in a horizontally heated rotating fluid

Published online by Cambridge University Press:  24 October 2008

P. G. Daniels  and
K. Stewartson
P. G. Daniels
Affiliation:
University College, London
K. Stewartson
Affiliation:
University College, London
Get access Rights & Permissions [Opens in a new window]

Abstract

Fluid is contained in a rotating annulus of rectangular cross-section which is subject to a radial temperature gradient along the base and is insulated around its upper surfaces. If E is an Ekman number, which is assumed small, a finite amplitude cellular motion of wavelength ∼ E⅓ develops near the inner sidewall of the annulus by an exchange process if the local Rayleigh number, R, exceeds its critical value Rc and the Prandtl number of the fluid, σ, is greater than a critical value, σc (Daniels and Stewartson(5)). In the present study we consider the remaining range of values 0 < σ < σc for which overstability is preferred, occurring at a value of the Rayleigh number, Rc0, less than Rc. Disturbances to the basic flow near the sidewall now oscillate in time with frequency ∼ E⅓ and are amplified if R exceeds Rc0, the vertical cellular velocity attaining values ∼ E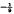 in a region of extent ∼ E 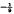near the sidewall. On the time-scale ∼ E 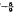disturbances take the form of two wave-like components which travel in opposite directions with the characteristic group velocity of the system. The first is simply convected away from the sidewall into the stably stratified interior and decays, while the second travels towards the sidewall where it is reflected. The reflexion coefficient is determined by the dynamics of an E⅓ boundary layer where an oscillatory motion is generated by the incident wave.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 83 , Issue 2 , March 1978 , pp. 329 - 345
Copyright
Copyright © Cambridge Philosophical Society 1978

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Chandrasekhar, S.Hydrodynamic and hydromagnetic stability (Oxford University Press, 1962).Google Scholar
(2)Daniels, P. G.Thermal convection in a differentially heated rotating fluid annulus. Geo. Fluid Dyn. 7 (1976), 296–330.Google Scholar
(3)Daniels, P. G.The effect of distant sidewalls on the transition to finite amplitude Beiiard convection. Proc. Roy. Soc. London A (1977).Google Scholar
(4)Daniels, P. G. and Stewartson, K.On the spatial oscillations of a horizontally heated rotating fluid. Math. Proc. Cambridge Philos. Soc. 81 (1977), 325–349.Google Scholar
(5)Daniels, P. G. and Stewartson, K.On the spatial oscillations of a horizontally heated rotating fluid II. Quart. J. Mech. Appl. Math. (1977).Google Scholar
(6)Hide, R. and Mason, P. J.Sloping convection in a rotating fluid. Advances in Physics 24 (1975), 47–100.Google Scholar