Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-25T02:30:18.320Z Has data issue: false hasContentIssue false
  • English
  • Français

Operators on the generalized entire sequences

Published online by Cambridge University Press:  24 October 2008

I. J. Maddox
I. J. Maddox
Affiliation:
Queen's University of Belfast
Get access Rights & Permissions [Opens in a new window]

Extract

Let p = (pk) and q = (qk) be any sequences of strictly positive numbers. Denote by c0(p) the set of all complex sequences x = (xk) such that 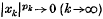. The Köthe–Toeplitz dual of c0(p) was determined in Theorem 6(4). In the case in which p∈l∞ (the space of all bounded sequences), c0(p) becomes a locally convex FK space under the paranorm 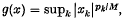where M = max (1, sup pk). It has been recently proved by Lascarides(3) that the following three properties are equivalent:

(a) p∈c0(i.e.pk → 0),

(b) c0(p) is perfect (in the sense of Köthe-Toeplitz duality),

(c) c0(p) has the Schur property (i.e. weak and strong sequential convergence are equivalent).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 71 , Issue 3 , May 1972 , pp. 491 - 494
Copyright
Copyright © Cambridge Philosophical Society 1972

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Brown, H. I.Entire methods of summation. Compositio Math. 21 (1969), 35–42.Google Scholar
(2)Iyer, V. G.On the space of integral functions. I. J. Indian Math. Soc. (2) 12 (1948), 13–30.Google Scholar
(3)Lascarides, C. G. A study of certain sequence spaces of Maddox and a generalization of a theorem of Iyer. Pacific J. Math. (to appear shortly).Google Scholar
(4)Maddox, I. J.Continuous and Köthe–Toeplitz duals of certain sequence spaces. Proc. Cambridge Philos. Soc. 65 (1969), 431–435.CrossRefGoogle Scholar
(5)Roles, J. W. Ph.D. thesis. University of Lancaster (1970).Google Scholar
(6)Roles, J. W. The characterization of certain classes of matrix transformations. J. London Math. Soc. (to appear shortly).Google Scholar
(7)Wilansky, A.Functional analysis (Blaisdell, New York, 1964).Google Scholar