No CrossRef data available.
Article contents
On the topology of the transversal slice of a quasi-homogeneous map germ
Part of:
Local theory
Published online by Cambridge University Press: 06 October 2023
Abstract
We consider a corank 1, finitely determined, quasi-homogeneous map germ f from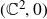 
$(\mathbb{C}^2,0)$ to 
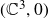$(\mathbb{C}^3,0)$. We describe the embedded topological type of a generic hyperplane section of 
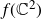$f(\mathbb{C}^2)$, denoted by 
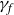$\gamma_f$, in terms of the weights and degrees of f. As a consequence, a necessary condition for a corank 1 finitely determined map germ 
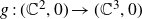$g\,{:}\,(\mathbb{C}^2,0)\rightarrow (\mathbb{C}^3,0)$ to be quasi-homogeneous is that the plane curve 
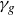$\gamma_g$ has either two or three characteristic exponents. As an application of our main result, we also show that any one-parameter unfolding 
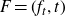$F=(f_t,t)$ of f which adds only terms of the same degrees as the degrees of f is Whitney equisingular.
MSC classification
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 176 , Issue 2 , March 2024 , pp. 339 - 359
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Cambridge Philosophical Society
References
Buchweitz, R.O. and Greuel, G.-M.. The milnor number and deformations of complex curve singularities. Invent. Math. 58 (1980), 241–281.Google Scholar
Callejas Bedregal, R., Houston, K. and Ruas, M.A.S.. Topological triviality of families of singular surfaces. Preprint (2006), arXiv:math/0611699v1.Google Scholar
Campillo, A.. Algebroid curves in positive characteristic. Lecture Notes in Math. 813 (Springer, 1980).CrossRefGoogle Scholar
Cohen, M.N.. Roots of formal power series and new theorems on riordan group elements. Preprint (2019), arXiv:1907.00116v1.Google Scholar
Damon, J.. Topological triviality and versality for subgroups of A and K II. Sufficient conditions and applications. Nonlinearity 5 (1992), 373–412.CrossRefGoogle Scholar
Decker, W., Greuel, G.-M., Pfister, G. and Schönemann, H.. Singular 4-0-2, A computer algebra system for polynomial computations. In: M. Kerber and M. Kohlhase (eds.), Symbolic Computation and Automated Reasoning. The Calculemus-2000 Symposium (2001), 227–233. Available at: http://www.singular.uni-kl.de.Google Scholar
Fernández de Bobadilla, J. and Pe Pereira, M.. Equisingularity at the normalisation. J. Topol. 88 (2008), 879–909.CrossRefGoogle Scholar
Gaffney, T.. Polar multiplicities and equisingularity of map germs. Topology 32 (1993), 185–223.CrossRefGoogle Scholar
Giles Flores, A., Silva, O.N. and Snoussi, J.. On tangency in equisingular families of curves and surfaces. Quart. J. Math. 71 (2020), 485–505.Google Scholar
Grauert, H. and Remmert, R.. Theory of stein spaces. Grundlehren Math. Wiss. 236 (Springer-Verlag, Berlin, 1979).CrossRefGoogle Scholar
Hernandes, M.E., Miranda, A.J. and Peñafort–Sanchis, G.. A presentation matrix algorithm for
$f_{\ast}\mathcal{O}_{X,x}$
. Topology Appl. 234 (2018), 440–451.CrossRefGoogle Scholar
$f_{\ast}\mathcal{O}_{X,x}$
. Topology Appl. 234 (2018), 440–451.CrossRefGoogle ScholarMarar, W.L. and Nuño–Ballesteros, J.J.. Slicing corank 1 map germs from
$\mathbb{C}^2$
to
$\mathbb{C}^3$
. Quart. J. Math. 65 (2014), 1375–1395.CrossRefGoogle Scholar
$\mathbb{C}^2$
to
$\mathbb{C}^3$
. Quart. J. Math. 65 (2014), 1375–1395.CrossRefGoogle ScholarMarar, W.L., Nuño–Ballesteros, J.J. and Peñafort–Sanchis, G.. Double point curves for corank 2 map germs from
$\mathbb{C}^2$
to
$\mathbb{C}^3$
. Topology Appl. 159 (2012), 526–536.Google Scholar
$\mathbb{C}^2$
to
$\mathbb{C}^3$
. Topology Appl. 159 (2012), 526–536.Google ScholarMarar, W.L. and Mond, D.. Multiple point schemes for corank 1 maps. J. London Math. Soc. 39 (1989), 553–567.CrossRefGoogle Scholar
Mather, J.N.. Stability of
$C^{\infty}$
mappings. VI: the nice dimensions. Lecture Notes in Math. 192 (Springer, Berlin, 1971), 207–253.CrossRefGoogle Scholar
$C^{\infty}$
mappings. VI: the nice dimensions. Lecture Notes in Math. 192 (Springer, Berlin, 1971), 207–253.CrossRefGoogle ScholarMond, D.. On the classification of germs of maps from
$\mathbb{R}^2$
to
$\mathbb{R}^3$
. Proc. London Math. Soc. 50
(3) (1985), 333–369.CrossRefGoogle Scholar
$\mathbb{R}^2$
to
$\mathbb{R}^3$
. Proc. London Math. Soc. 50
(3) (1985), 333–369.CrossRefGoogle ScholarMond, D.. Some remarks on the geometry and classification of germs of map from surfaces to 3-space. Topology 26 (1987), 361–383.CrossRefGoogle Scholar
Mond, D.. The number of vanishing cycles for a quasihomogeneous mapping from
$\mathbb{C}^2$
to
$\mathbb{C}^3$
. Quart. J. Math. 42
(2) (1991), 335–345.CrossRefGoogle Scholar
$\mathbb{C}^2$
to
$\mathbb{C}^3$
. Quart. J. Math. 42
(2) (1991), 335–345.CrossRefGoogle ScholarMond, D. and Nuño–Ballesteros, J.J.. Singularities of mappings. Grundlehren Math. Wiss. 357 (Springer-Verlag, New York, 20202020), 335–345.Google Scholar
Mond, D. and Pellikaan, R.. Fitting ideals and multiple points of analytic mappings. Lecture Notes in Math. 1414 (1987), 107–161.Google Scholar
Pellikaan, R.. Hypersurface singularities and resolutions of Jacobi modules. Dissertation. Rijksuniversiteit te Utrecht (1985).Google Scholar
Ruas, M.A.S. and Silva, O.N.. Whitney equisingularity of families of surfaces in
$\mathbb{C}^3$
. Math. Proc. Camb. Phil. Soc. 166 (2019), 353–369.CrossRefGoogle Scholar
$\mathbb{C}^3$
. Math. Proc. Camb. Phil. Soc. 166 (2019), 353–369.CrossRefGoogle ScholarSaito, K.. Quasihomogene isolierte Singularitäten von Hyperflächen. Invent. Math. 14 (1971), 123–142.CrossRefGoogle Scholar
Silva, O.N.. On invariants of generic slices of weighted homogeneous corank 1 map germs from the plane to 3-space. Bull. Braz. Math. Soc. 52 (2021), 663–677.CrossRefGoogle Scholar
Silva, O.N.. Surfaces with non-isolated singularities. PhD. thesis. Universidade de São Paulo. Avalaible at http://www.teses.usp.br/teses/disponiveis/55/55135/tde-10052017-085440/pt-br.php (2017).Google Scholar
Wall, C.T.C.. Finite determinacy of smooth map germs. Bull. London Math. Soc. 13 (1981), 481–539.CrossRefGoogle Scholar