Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T17:01:29.399Z Has data issue: false hasContentIssue false
  • English
  • Français

On the stability of the three-phase synchronous motor

Published online by Cambridge University Press:  24 October 2008

W. H. Ingram
W. H. Ingram
Affiliation:
School of Engineering, Columbia University
Get access Rights & Permissions [Opens in a new window]

Extract

A three-phase star-connected alternating-current motor of simplest type, connected to busbars maintained at sinusoidal potentials e1, e2 and e3 with respect to the star-point and connected to a shaft load which exerts a reactive torque f on the rotor, is dynamically specified by the following functions:

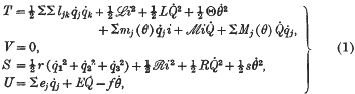
where the 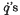are the armature currents in the three phases, i is the current in the amortisseur circuit, Q the current in the field circuit, θ the rotor position angle, T the kinetic energy, V the potential energy, S the Rayleigh dissipation and U the activity of the external forces on the machine. The self-inductances of the armature circuits and the mutual inductances between them are assumed to be constant.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 29 , Issue 4 , 30 October 1933 , pp. 528 - 535
Copyright
Copyright © Cambridge Philosophical Society 1933

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

† See Ingram, , Proc. Camb. Phil. Soc. 28 (1932), 106CrossRefGoogle Scholar. The formula on p. 108 holds in form when saturation is taken into account, but then the position of the rotor is not accurately given by ψ.

† By a discussion of the determinant given on p. 616 of the Electrician for May 12th, 1933. Routh's criterion has been given a convenient determinantal form by Frazer, and Duncan, , Proc. Roy. Soc. A, 124 (1929), 642.CrossRefGoogle Scholar

‡ Taken from Miles Walker: Specification and Design of Dynamo-Electric Machines, p. 404. For this machine, the following values are taken or computed: r = 0·0004 ohm, l 11 = 3·4 × 10−4, l 12 = − 1·5 × 10−4, l* = 5·0 × 10−4, M 0 = 0·015 and M 0 = 1·0 × 10−4 henrys.

† Cf. Nickle, and Pierce, , Trans. Am. Inst. El. Engrs. 49 (1930), p. 34.Google Scholar

‡ Cf. Moulton, , Periodic Orbits, p. 23.Google Scholar