No CrossRef data available.
On the representation of rational sections of the Grassmannian of lines of five dimensions
Published online by Cambridge University Press: 24 October 2008
Extract
The Grassmannian, 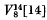 of lines of S5 and also its sections by general spaces of 13, 12, 11 and 10 dimensions were shown to be rational by Severi. The section
of lines of S5 and also its sections by general spaces of 13, 12, 11 and 10 dimensions were shown to be rational by Severi. The section 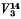 by a general S9 is, by a result of Fano, birationally equivalent to a non-singular cubic primal of S4 and hence is probably not rational.
by a general S9 is, by a result of Fano, birationally equivalent to a non-singular cubic primal of S4 and hence is probably not rational.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 47 , Issue 2 , April 1951 , pp. 305 - 308
- Copyright
- Copyright © Cambridge Philosophical Society 1951
References
* Severi, F., Ann. Mat. pura appl. (3), 24 (1915), 89–120.CrossRefGoogle Scholar
† Fano, G., R. C. Accad. Lincei, (6), 11 (1930), 329–35.Google Scholar
‡ Semple, J. G., Proc. London Math. Soc. (2), 32 (1931), 200–21.CrossRefGoogle Scholar
* A similar representation holds for the intersection of two general quadrics in any space S r(r ≥ 4). For r = 4, Λ consists of five points; for r = 5, Λ is a curve 2C 5, and so on. See, for example, Semple, and Roth, , Introduction to algebraic geometry, p. 172Google Scholar, where the case r = 5 is considered.
* Severi, F., Mem. R. Accad. Torino, (2), 52 (1903), 61.Google Scholar
† Roth, L., Proc. Cambridge Phil. Soc. 46 (1950), 423.CrossRefGoogle Scholar
‡ Roth, L., Proc. Cambridge Phil. Soc. 29 (1933), 184.CrossRefGoogle Scholar
§ Fano, G., Ann. Mat. pura appl. (3), 24 (1915), 49–88.CrossRefGoogle Scholar
* A result due to Roth and contained in a paper in course of publication in the R. C. Semin. mat. Univ. Roma.


