On the relative merits of correlated and importance sampling for Monte Carlo integration

Extract

Given a totally finite measure space (S, S, μ) and two μ-integrable, non-negative functions f(x) and φ(x) defined in S, such that when

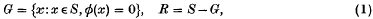
then

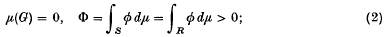
we define correlated sampling as the technique of estimating

by sampling an estimator function

where ξ is uniformly distributed in S with respect to μ (i.e. for any T ∈ S, p(T) = μ(T)/μ(S) is the probability that ξ lies in T): and importance sampling as estimating L by sampling the estimator function

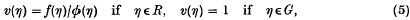
where η is distributed in S with probability density φ(x)/Φ

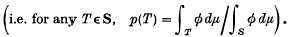
Then, clearly,

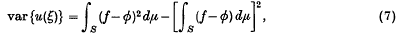
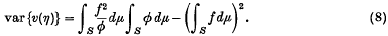
It follows that υ(ξ) and ν(η) are both unbiased estimators of L, and that their variances can both be made to approach zero arbitrarily closely by making φ(x) a sufficiently close approximation to f(x).