Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Obi, Chike
1979.
Analytical theory of non-linear oscillations.
Annali di Matematica Pura ed Applicata,
Vol. 120,
Issue. 1,
p.
139.


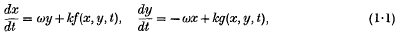
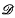 and are periodic in
and are periodic in