Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-23T18:31:04.705Z Has data issue: false hasContentIssue false
  • English
  • Français

On the rate of Poisson convergence

Published online by Cambridge University Press:  24 October 2008

A. D. Barbour  and
Peter Hall
A. D. Barbour
Affiliation:
Gonville and Caius College, Cambridge CB2 1TA
Peter Hall
Affiliation:
Department of Statistics, The Faculties, Australian National University
Get access Rights & Permissions [Opens in a new window]

Extract

Let X1, …, Xn be independent Bernoulli random variables, and let pi = P[Xi = 1], λ = Σi=1n pi and Σi=1n Xi. Successively improved estimates of the total variation distance between the distribution ℒ(W) of W and a Poisson distribution Pλ with mean λ have been obtained by Prohorov[5], Le Cam [4], Kerstan[3], Vervaat[8], Chen [2], Serfling[7] and Romanowska[6]. Prohorov, Vervaat and Romanowska discussed only the case of identically distributed Xi's, whereas Chen and Serfling were primarily interested in more general, dependent sequences. Under the present hypotheses, the following inequalities, here expressed in terms of the total variation distance

were established respectively by Le Cam, Kerstan and Chen:

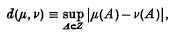
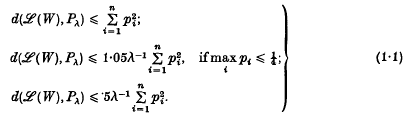
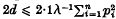(Kerstan's published estimate of ([3], p.174, equation (1)) is a misprint for 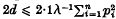, the constant 2·1 appearing twice on p. 175 of his paper.) Here, we use Chen's [2] elegant adaptation of Stein's method to improve hte estimates given in (1·1), and we complement these estimates with a reverse inequality expressed in similar terms. Second order estimates, and the case of more general non-negative integer valued X's, are also discussed.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 95 , Issue 3 , May 1984 , pp. 473 - 480
Copyright
Copyright © Cambridge Philosophical Society 1984

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Barbour, A. D. and Eagleson, G. K.. Poisson approximation for some statistics based on exchangeable trials. Adv. in Appl. Probab. 15 (1983), 585–600.CrossRefGoogle Scholar
[2]Chen, L. H. Y.. Poisson approximation for dependent trials. Ann. Probab. 3 (1975), 534–545.CrossRefGoogle Scholar
[3]Kebstan, J.. Verallgemeinerung eines Satzes von Procharov und Le Cam. Z. Wahrsch. Verw. Gebiete 2 (1964), 173–179.CrossRefGoogle Scholar
[4]Cam, L. Le. An approximation theorem for the Poisson binomial distribution. Pacific J. Math. 10 (1960), 1181–1197.Google Scholar
[5]Prohorov, J. V.. Asymptotic behaviour of the binomial distribution. Uspekhi Mat. Nauk 8 (1953), 135–142.Google Scholar
[6]Romanowska, M.. A note on the upper bound for the distance in total variation between the binomial and the Poisson distribution. Statist. Neerlandica 31 (1977), 127–130.CrossRefGoogle Scholar
[7]Serfling, R. J.. A general Poisson approximation theorem. Ann. Probab. 3 (1975), 726–731.CrossRefGoogle Scholar
[8]Vervaat, W.. Upper bounds for the distance in total variation between the binomial or negative binomial and the Poisson distribution. Statist. Neerlandica 23 (1969), 79–86.Google Scholar