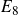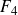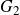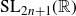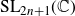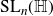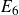1. Introduction
If two residually finite groups are commensurable, so are the profinite completions. Thus for any class
![]() $\mathcal{C}$
of residually finite groups, the converse rigidity question arises: if two groups from
$\mathcal{C}$
of residually finite groups, the converse rigidity question arises: if two groups from
![]() $\mathcal{C}$
are profinitely commensurable, are they abstractly commensurable? It is known that arithmetic groups with the congruence subgroup property can be used to construct lattices in higher rank Lie groups which are profinitely isomorphic but not abstractly isomorphic; see [
Reference Aka1
,
Reference Aka2
,
Reference Kammeyer11
,
Reference Lubotzky17
]. Aka showed [
Reference Aka2
] that the profinite isomorphism class of a higher rank lattice contains only finitely many abstract commensurability types of lattices. Here we address the question whether every simple Lie group G of higher rank actually admits profinitely isomorphic but non-commensurable lattices. The flexibility of the familiar construction might be taken as evidence, that the answer should be affirmative. However, it turns out that the question is more delicate, and the answer depends on G.
$\mathcal{C}$
are profinitely commensurable, are they abstractly commensurable? It is known that arithmetic groups with the congruence subgroup property can be used to construct lattices in higher rank Lie groups which are profinitely isomorphic but not abstractly isomorphic; see [
Reference Aka1
,
Reference Aka2
,
Reference Kammeyer11
,
Reference Lubotzky17
]. Aka showed [
Reference Aka2
] that the profinite isomorphism class of a higher rank lattice contains only finitely many abstract commensurability types of lattices. Here we address the question whether every simple Lie group G of higher rank actually admits profinitely isomorphic but non-commensurable lattices. The flexibility of the familiar construction might be taken as evidence, that the answer should be affirmative. However, it turns out that the question is more delicate, and the answer depends on G.
Theorem 1·1. Let G be a connected simple higher rank Lie group with finite center which is:
-
(i) neither a complex form of type
 $E_8$
,
$E_8$
,
 $F_4$
, or
$F_4$
, or
 $G_2$
;
$G_2$
; -
(ii) nor a real or complex form of type
 $E_6$
;
$E_6$
; -
(iii) nor locally isomorphic to
 $\text{SL}_{2m+1}(\mathbb{R})$
,
$\text{SL}_{2m+1}(\mathbb{R})$
,
 $\text{SL}_{2m+1}(\mathbb{C})$
, or
$\text{SL}_{2m+1}(\mathbb{C})$
, or
 $\text{SL}_m(\mathbb{H})$
.
$\text{SL}_m(\mathbb{H})$
.
Then for each
![]() $n \ge 2$
, there exist cocompact lattices
$n \ge 2$
, there exist cocompact lattices
![]() $\Gamma_1, \ldots, \Gamma_n \subset G$
which are pairwise profinitely isomorphic but pairwise not commensurable.
$\Gamma_1, \ldots, \Gamma_n \subset G$
which are pairwise profinitely isomorphic but pairwise not commensurable.
So in most cases rigidity fails in a strong sense but the first three groups form a surprising exception.
Theorem 1·2. Let G be a connected simple complex Lie group of type
![]() $E_8$
,
$E_8$
,
![]() $F_4$
, or
$F_4$
, or
![]() $G_2$
and let
$G_2$
and let
![]() $\Gamma_1, \Gamma_2 \subset G$
be lattices such that
$\Gamma_1, \Gamma_2 \subset G$
be lattices such that
![]() $\Gamma_1$
is profinitely commensurable with
$\Gamma_1$
is profinitely commensurable with
![]() $\Gamma_2$
. Then
$\Gamma_2$
. Then
![]() $\Gamma_1$
is commensurable with
$\Gamma_1$
is commensurable with
![]() $\Gamma_2$
.
$\Gamma_2$
.
Going through the census, the complete list of higher rank simple Lie groups currently not covered by either Theorem 1·1 or Theorem 1·2 is given by
![]() $\textrm{SL}_{2m-1}(\mathbb{R})$
and
$\textrm{SL}_{2m-1}(\mathbb{R})$
and
![]() $\textrm{SL}_{2m-1}(\mathbb{C})$
, and
$\textrm{SL}_{2m-1}(\mathbb{C})$
, and
![]() $\textrm{SL}_m(\mathbb{H})$
for
$\textrm{SL}_m(\mathbb{H})$
for
![]() $m \ge 2$
, as well as all the
$m \ge 2$
, as well as all the
![]() $E_6$
-forms:
$E_6$
-forms:
![]() $E_{6(6)}$
,
$E_{6(6)}$
,
![]() $E_{6(2)}$
,
$E_{6(2)}$
,
![]() $E_{6({-}14)}$
,
$E_{6({-}14)}$
,
![]() $E_{6({-}26)}$
, and
$E_{6({-}26)}$
, and
![]() $E_6(\mathbb{C})$
. If the congruence subgroup property was known to hold true for higher rank groups of type
$E_6(\mathbb{C})$
. If the congruence subgroup property was known to hold true for higher rank groups of type
![]() $A_n$
and
$A_n$
and
![]() $E_6$
, all these groups would likewise fall under the conclusion of Theorem 1·1. For instance, the non-isomorphic but locally isomorphic algebraic groups of types
$E_6$
, all these groups would likewise fall under the conclusion of Theorem 1·1. For instance, the non-isomorphic but locally isomorphic algebraic groups of types
![]() $A_n$
,
$A_n$
,
![]() $D_{2n+1}$
and
$D_{2n+1}$
and
![]() $E_6$
in [
Reference Prasad and Rapinchuk25
, theorem 9·12] would give rise to examples. Let us stress however that our result is unconditional. Though the congruence subgroup problem is generally open in type
$E_6$
in [
Reference Prasad and Rapinchuk25
, theorem 9·12] would give rise to examples. Let us stress however that our result is unconditional. Though the congruence subgroup problem is generally open in type
![]() $A_n$
and
$A_n$
and
![]() $D_4$
, we were able to exploit the partial progress made in the literature to the extent that the type
$D_4$
, we were able to exploit the partial progress made in the literature to the extent that the type
![]() $A_n$
groups
$A_n$
groups
![]() $\textrm{SL}_{2m}(\mathbb{R})$
and
$\textrm{SL}_{2m}(\mathbb{R})$
and
![]() $\textrm{SL}_{2m}(\mathbb{C})$
, as well as
$\textrm{SL}_{2m}(\mathbb{C})$
, as well as
![]() $\textrm{SU}(p,q)$
for
$\textrm{SU}(p,q)$
for
![]() $p,q \ge 2$
, and all the type
$p,q \ge 2$
, and all the type
![]() $D_4$
groups
$D_4$
groups
![]() $\textrm{SO}^0(6,2)$
,
$\textrm{SO}^0(6,2)$
,
![]() $\textrm{SO}^0(5,3)$
,
$\textrm{SO}^0(5,3)$
,
![]() $\textrm{SO}^0(4,4)$
, and
$\textrm{SO}^0(4,4)$
, and
![]() $\textrm{SO}^*(8)$
are included in Theorem 1·1.
$\textrm{SO}^*(8)$
are included in Theorem 1·1.
The lattices constructed here are intrinsically cocompact, since our approach is based on arithmetic groups defined over number fields of large degree. The construction of profinitely isomorphic non-cocompact lattices requires different methods; e.g., similar to the construction in [
Reference Prasad and Rapinchuk25
, theorem 9·12]. In Proposition 3·1 we illustrate this by showing that
![]() $\textrm{SL}_m(\mathbb{R})$
,
$\textrm{SL}_m(\mathbb{R})$
,
![]() $\textrm{SL}_m(\mathbb{C})$
and
$\textrm{SL}_m(\mathbb{C})$
and
![]() $\textrm{SL}_m(\mathbb{H})$
, where
$\textrm{SL}_m(\mathbb{H})$
, where
![]() $m\geq 6$
is composite, admit profinitely isomorphic, non-commensurable, non-cocompact lattices.
$m\geq 6$
is composite, admit profinitely isomorphic, non-commensurable, non-cocompact lattices.
For the various types of G, we employ varying methods to construct the families
![]() $\Gamma_1, \ldots, \Gamma_n \subset G$
of profinitely isomorphic but non-commensurable lattices in Theorem 1·1. There does not seem to be a uniform approach that would work in all cases. This is however different for the question that is more commonly addressed under the term profinite rigidity in the literature: if two groups have isomorphic profinite completions, are they isomorphic? Here the congruence subgroup property, whenever it is known to hold for G, can be used to construct profinitely isomorphic but non-isomorphic congruence subgroups in a uniform way.
$\Gamma_1, \ldots, \Gamma_n \subset G$
of profinitely isomorphic but non-commensurable lattices in Theorem 1·1. There does not seem to be a uniform approach that would work in all cases. This is however different for the question that is more commonly addressed under the term profinite rigidity in the literature: if two groups have isomorphic profinite completions, are they isomorphic? Here the congruence subgroup property, whenever it is known to hold for G, can be used to construct profinitely isomorphic but non-isomorphic congruence subgroups in a uniform way.
Theorem 1·3. Let G be a higher rank connected simple Lie group with trivial center and not isomorphic to
![]() $\text{PSL}_m(\mathbb{H})$
or to a complex or real form of type
$\text{PSL}_m(\mathbb{H})$
or to a complex or real form of type
![]() $E_6$
. Then there exist arbitrarily many cocompact lattices in G which are pairwise profinitely isomorphic but pairwise not isomorphic.
$E_6$
. Then there exist arbitrarily many cocompact lattices in G which are pairwise profinitely isomorphic but pairwise not isomorphic.
Again, the exceptions can likely be omitted. They only owe to the incomplete status of the congruence subgroup problem. We see that profinite rigidity in the usual sense also fails for
![]() $E_8(\mathbb{C})$
,
$E_8(\mathbb{C})$
,
![]() $F_4(\mathbb{C})$
, and
$F_4(\mathbb{C})$
, and
![]() $G_2(\mathbb{C})$
, and most likey fails for lattices in all higher rank simple Lie groups. However, the lattices we construct in the proof of Theorem 1·3 are arithmetic subgroups of different congruence levels. While they are not isomorphic, they are commensurable which is why they should not really be considered as distinct lattices. This is why we find it more on point to ask for profinitely commensurable lattices in G of higher rank which are not commensurable.
$G_2(\mathbb{C})$
, and most likey fails for lattices in all higher rank simple Lie groups. However, the lattices we construct in the proof of Theorem 1·3 are arithmetic subgroups of different congruence levels. While they are not isomorphic, they are commensurable which is why they should not really be considered as distinct lattices. This is why we find it more on point to ask for profinitely commensurable lattices in G of higher rank which are not commensurable.
Let us remark that profinite rigidity questions are typically only posed for residually finite groups to avoid trivial examples like
![]() $\widehat{\Gamma \times \Lambda} \cong \widehat{\Gamma} \times \widehat{\Lambda} \cong \widehat{\Gamma}$
for any group
$\widehat{\Gamma \times \Lambda} \cong \widehat{\Gamma} \times \widehat{\Lambda} \cong \widehat{\Gamma}$
for any group
![]() $\Gamma$
and any infinite simple group
$\Gamma$
and any infinite simple group
![]() $\Lambda$
. Most simple Lie groups with finite center are linear and hence lattices are residually finite. However, there are simple Lie groups with finite center which admit lattices that are not residually finite. An example is given by the four-fold covering of
$\Lambda$
. Most simple Lie groups with finite center are linear and hence lattices are residually finite. However, there are simple Lie groups with finite center which admit lattices that are not residually finite. An example is given by the four-fold covering of
![]() $\textrm{Sp}_n(\mathbb{R})$
[
Reference Deligne7
]. In these cases it is nevertheless reasonable to consider the profinite completion because the kernel of the completion homomorphism
$\textrm{Sp}_n(\mathbb{R})$
[
Reference Deligne7
]. In these cases it is nevertheless reasonable to consider the profinite completion because the kernel of the completion homomorphism
![]() $\Gamma \to \widehat{\Gamma}$
is merely a finite central subgroup.
$\Gamma \to \widehat{\Gamma}$
is merely a finite central subgroup.
Profinite rigidity of groups and related problems receive considerable attention in current research activities; see [ Reference Reid26 ] for a survey. Fundamental groups of 3-manifolds, see [ Reference Bridson, McReynolds, Reid and Spitler5 ] and references therein, and lattices in Lie groups [ Reference Kammeyer, Kionke, Raimbault and Sauer12 , Reference Stover30 ] are the main objects of interest.
We briefly sketch the proofs of Theorems 1·1 and 1·2. As we just commented, the proof of Theorem 1·1 splits up into various cases. At this point, we shall only present the most common line of arguments that works for most real forms G. We may assume
![]() $G = \textbf{G}(\mathbb{R})$
for an absolutely simple, simply connected algebraic
$G = \textbf{G}(\mathbb{R})$
for an absolutely simple, simply connected algebraic
![]() $\mathbb{R}$
-group
$\mathbb{R}$
-group
![]() $\textbf{G}$
. We construct linear algebraic groups
$\textbf{G}$
. We construct linear algebraic groups
![]() $\textbf{G}_1,\dots,\textbf{G}_n$
over a suitable totally real number field k such that
$\textbf{G}_1,\dots,\textbf{G}_n$
over a suitable totally real number field k such that
![]() $\textbf{G}_i$
is isomorphic to
$\textbf{G}_i$
is isomorphic to
![]() $\textbf{G}$
at exactly one real place of k and is compact at all other real places. The lattices arise as arithmetic subgroups
$\textbf{G}$
at exactly one real place of k and is compact at all other real places. The lattices arise as arithmetic subgroups
![]() $\Gamma_i \subseteq \textbf{G}_i(k)$
, ensuring that the congruence subgroup property holds for the groups
$\Gamma_i \subseteq \textbf{G}_i(k)$
, ensuring that the congruence subgroup property holds for the groups
![]() $\textbf{G}_i$
(special attention is needed in type
$\textbf{G}_i$
(special attention is needed in type
![]() $A_m$
and
$A_m$
and
![]() $D_4$
). The core of the argument is a local-global principle which almost allows us to achieve that the groups
$D_4$
). The core of the argument is a local-global principle which almost allows us to achieve that the groups
![]() $\textbf{G}_1,\dots,\textbf{G}_n$
are isomorphic at all finite places of k. If the groups
$\textbf{G}_1,\dots,\textbf{G}_n$
are isomorphic at all finite places of k. If the groups
![]() $\textbf{G}_i$
were isomorphic at all finite places of k, then the congruence subgroup property implies that the groups are profinitely commensurable (by Theorem 2·5 and Lemma 2·6). If the field k has no non-trivial automorphisms, then Margulis superrigidity can be used to deduce that the arithmetic lattices are not commensurable (Theorem 2·7). There is however a caveat: The local-global principle only allows to control the isomorphism type except for one finite place. But since there exists only a finite number of possible
$\textbf{G}_i$
were isomorphic at all finite places of k, then the congruence subgroup property implies that the groups are profinitely commensurable (by Theorem 2·5 and Lemma 2·6). If the field k has no non-trivial automorphisms, then Margulis superrigidity can be used to deduce that the arithmetic lattices are not commensurable (Theorem 2·7). There is however a caveat: The local-global principle only allows to control the isomorphism type except for one finite place. But since there exists only a finite number of possible
![]() $\mathfrak{p}$
-adic types for the groups
$\mathfrak{p}$
-adic types for the groups
![]() $\textbf{G}_i$
, we can infer from Dirichlet’s box principle that for arbitrary large n, arbitrarily many of the groups
$\textbf{G}_i$
, we can infer from Dirichlet’s box principle that for arbitrary large n, arbitrarily many of the groups
![]() $\textbf{G}_i$
are isomorphic at every finite place.
$\textbf{G}_i$
are isomorphic at every finite place.
To prove Theorem 1·2, we apply Margulis arithmeticity to conclude that for
![]() $i = 1,2$
,
$i = 1,2$
,
![]() $\Gamma_i$
is commensurable with an arithmetic subgroup in a
$\Gamma_i$
is commensurable with an arithmetic subgroup in a
![]() $k_i$
-group
$k_i$
-group
![]() $\textbf{G}_{\textbf{i}}$
over some number field
$\textbf{G}_{\textbf{i}}$
over some number field
![]() $k_i$
with precisely one complex place such that
$k_i$
with precisely one complex place such that
![]() $\textbf{G}_{\textbf{i}}$
is anisotropic at all real places of
$\textbf{G}_{\textbf{i}}$
is anisotropic at all real places of
![]() $k_i$
. The congruence subgroup property, which is known in the exceptional types under consideration, effects that
$k_i$
. The congruence subgroup property, which is known in the exceptional types under consideration, effects that
![]() $\widehat{\Gamma_i}$
is commensurable with the finite adele points
$\widehat{\Gamma_i}$
is commensurable with the finite adele points
![]() $\textbf{G}_{\textbf{i}}\big(\mathbb{A}^f_{k_i}\big)$
of
$\textbf{G}_{\textbf{i}}\big(\mathbb{A}^f_{k_i}\big)$
of
![]() $\textbf{G}_{\textbf{i}}$
. Hence
$\textbf{G}_{\textbf{i}}$
. Hence
![]() $\textbf{G}_{\textbf{1}}\big(\mathbb{A}^f_{k_1}\big)$
is commensurable with
$\textbf{G}_{\textbf{1}}\big(\mathbb{A}^f_{k_1}\big)$
is commensurable with
![]() $\textbf{G}_{\textbf{2}}\big(\mathbb{A}^f_{k_2}\big)$
from which we conclude that the number fields
$\textbf{G}_{\textbf{2}}\big(\mathbb{A}^f_{k_2}\big)$
from which we conclude that the number fields
![]() $k_1$
and
$k_1$
and
![]() $k_2$
are arithmetically equivalent, meaning they have equal Dedekind zeta function. There exists a myriad of arithmetically equivalent number fields, also among totally real ones, which are not isomorphic. However, a theorem due to Chinburg–Hamilton–Long–Reid says that arithmetically equivalent number fields with precisely one complex place are isomorphic [
Reference Chinburg, Hamilton, Long and Reid6
, corollary 1·4]. We conclude that
$k_2$
are arithmetically equivalent, meaning they have equal Dedekind zeta function. There exists a myriad of arithmetically equivalent number fields, also among totally real ones, which are not isomorphic. However, a theorem due to Chinburg–Hamilton–Long–Reid says that arithmetically equivalent number fields with precisely one complex place are isomorphic [
Reference Chinburg, Hamilton, Long and Reid6
, corollary 1·4]. We conclude that
![]() $\textbf{G}_{\textbf{2}}$
is a
$\textbf{G}_{\textbf{2}}$
is a
![]() $k_1$
-twist of
$k_1$
-twist of
![]() $\textbf{G}_{\textbf{1}}$
. These are classified by the noncommutative Galois cohomology set
$\textbf{G}_{\textbf{1}}$
. These are classified by the noncommutative Galois cohomology set
![]() $H^1(k_1, \textbf{G}_{\textbf{1}})$
because
$H^1(k_1, \textbf{G}_{\textbf{1}})$
because
![]() $\textbf{G}_{\textbf{1}}$
has trivial center and trivial outer automorphism group. The Hasse principle for simply connected groups in combination with M. Kneser’s vanishing result for Galois cohomology over
$\textbf{G}_{\textbf{1}}$
has trivial center and trivial outer automorphism group. The Hasse principle for simply connected groups in combination with M. Kneser’s vanishing result for Galois cohomology over
![]() $\mathfrak{p}$
-adic fields therefore implies that
$\mathfrak{p}$
-adic fields therefore implies that
![]() $\textbf{G}_1$
is actually
$\textbf{G}_1$
is actually
![]() $k_1$
-isomorphic to
$k_1$
-isomorphic to
![]() $\textbf{G}_2$
, hence
$\textbf{G}_2$
, hence
![]() $\Gamma_1$
is commensurable with
$\Gamma_1$
is commensurable with
![]() $\Gamma_2$
.
$\Gamma_2$
.
2. Preliminaries
2·1. Notation
Let k be an algebraic number field. The set of places of k is denoted by
![]() $V(k) = V_\infty(k) \cup V_f(k)$
; it is the union of the set of archimedean places
$V(k) = V_\infty(k) \cup V_f(k)$
; it is the union of the set of archimedean places
![]() $V_\infty(k)$
and the set of finite places
$V_\infty(k)$
and the set of finite places
![]() $V_f(k)$
. The completion of k at
$V_f(k)$
. The completion of k at
![]() $v \in V(k)$
is denoted by
$v \in V(k)$
is denoted by
![]() $k_v$
. The ring of adeles (respectively of finite adeles) of k is
$k_v$
. The ring of adeles (respectively of finite adeles) of k is
![]() $\mathbb{A}_k$
$\mathbb{A}_k$
![]() $\big($
resp.
$\big($
resp.
![]() $\mathbb{A}_k^f\big)$
.
$\mathbb{A}_k^f\big)$
.
2·2. Number fields without automorphisms
The following result is well-known; e.g., [ Reference Milne and Suh19 , proposition 2·3].
Lemma 2·1. There are totally real number fields of arbitrarily large degree over
![]() $\mathbb{Q}$
with trivial automorphism group.
$\mathbb{Q}$
with trivial automorphism group.
Proof. For (arbitrarily large)
![]() $n \ge 3$
, let
$n \ge 3$
, let
![]() $K/\mathbb{Q}$
be a totally real Galois extension with Galois group
$K/\mathbb{Q}$
be a totally real Galois extension with Galois group
![]() $\textrm{Gal}(K/\mathbb{Q}) \cong S_n$
. Let
$\textrm{Gal}(K/\mathbb{Q}) \cong S_n$
. Let
![]() $H \leq \textrm{Gal}(K/\mathbb{Q})$
be a subgroup isomorphic to
$H \leq \textrm{Gal}(K/\mathbb{Q})$
be a subgroup isomorphic to
![]() $S_{n-1}$
. The fixed field
$S_{n-1}$
. The fixed field
![]() $k = K^H$
is totally real,
$k = K^H$
is totally real,
![]() $[k\,:\,\mathbb{Q}] = n$
and k has a trivial automorphism group. Indeed, an automorphism of k extended to
$[k\,:\,\mathbb{Q}] = n$
and k has a trivial automorphism group. Indeed, an automorphism of k extended to
![]() $K/\mathbb{Q}$
normalizes H but
$K/\mathbb{Q}$
normalizes H but
![]() $S_{n-1}$
is self-normalising in
$S_{n-1}$
is self-normalising in
![]() $S_n$
.
$S_n$
.
Similarly, there is the following result for “almost” totally real fields.
Lemma 2·2. There are number fields of arbitrarily large degree over
![]() $\mathbb{Q}$
with precisely one complex place and with trivial automorphism group.
$\mathbb{Q}$
with precisely one complex place and with trivial automorphism group.
Proof. Fix a prime number
![]() $p > 2$
and an irreducible rational polynomial P of degree p with exactly two non-real roots. Let K be the splitting field of P with Galois group
$p > 2$
and an irreducible rational polynomial P of degree p with exactly two non-real roots. Let K be the splitting field of P with Galois group
![]() $G \subseteq S_p$
. Given
$G \subseteq S_p$
. Given
![]() $a \in K$
with
$a \in K$
with
![]() $P(a)=0$
, the subgroup
$P(a)=0$
, the subgroup
![]() $H \le G$
corresponding to
$H \le G$
corresponding to
![]() $k = \mathbb{Q}(a)$
has index p. So the group
$k = \mathbb{Q}(a)$
has index p. So the group
![]() $G \subseteq S_p$
contains an element of order p which must be a full p-cycle because p is prime. Moreover, the non-real roots of P are complex conjugates of one another, hence complex conjugation exhibits a nontrivial transposition in G. A symmetric group of prime order is generated by any full cycle and any transposition, so
$G \subseteq S_p$
contains an element of order p which must be a full p-cycle because p is prime. Moreover, the non-real roots of P are complex conjugates of one another, hence complex conjugation exhibits a nontrivial transposition in G. A symmetric group of prime order is generated by any full cycle and any transposition, so
![]() $G = S_p$
. We observe (as in Lemma 2·1) that the stabilizer H of a is actually self-normalising. Hence
$G = S_p$
. We observe (as in Lemma 2·1) that the stabilizer H of a is actually self-normalising. Hence
![]() $k = \mathbb{Q}(a)$
has trivial automorphism group.
$k = \mathbb{Q}(a)$
has trivial automorphism group.
2·3. Finite coverings of Lie groups
The following lemma will be applied to reduce the proof to the case where the Lie group G is given by the
![]() $\mathbb{R}$
- or
$\mathbb{R}$
- or
![]() $\mathbb{C}$
-points of a linear algebraic group.
$\mathbb{C}$
-points of a linear algebraic group.
Lemma 2·3. Let
![]() $f \colon G_1 \to G$
and
$f \colon G_1 \to G$
and
![]() $g \colon G \to G_0$
be homomorphisms of Lie groups with finite kernels. Assume that G is linear. If G possesses n cocompact lattices which are pairwise profinitely commensurable but pairwise not commensurable, then the same holds true for
$g \colon G \to G_0$
be homomorphisms of Lie groups with finite kernels. Assume that G is linear. If G possesses n cocompact lattices which are pairwise profinitely commensurable but pairwise not commensurable, then the same holds true for
![]() $G_1$
and
$G_1$
and
![]() $G_0$
.
$G_0$
.
Proof. The linearity will only be used to ensure that all lattices in G are residually finite. It suffices to treat the case
![]() $n = 2$
. Let
$n = 2$
. Let
![]() $\Gamma_1, \Gamma_2 \subseteq G$
be two non-commensurable, profinitely commensurable lattices. Then
$\Gamma_1, \Gamma_2 \subseteq G$
be two non-commensurable, profinitely commensurable lattices. Then
![]() $\Delta_i= f^{-1}(\Gamma_i)$
is a cocompact lattice in
$\Delta_i= f^{-1}(\Gamma_i)$
is a cocompact lattice in
![]() $G_1$
. Let
$G_1$
. Let
![]() $K_i \subseteq \Delta_i$
be the kernel of the completion
$K_i \subseteq \Delta_i$
be the kernel of the completion
![]() $\Delta_i \to \widehat{\Delta}_i$
. Since
$\Delta_i \to \widehat{\Delta}_i$
. Since
![]() $\Gamma_i$
is residually finite,
$\Gamma_i$
is residually finite,
![]() $K_i \subseteq \ker\!(f)$
. Since
$K_i \subseteq \ker\!(f)$
. Since
![]() $\ker\!(f)$
is finite, there is a finite index normal subgroup
$\ker\!(f)$
is finite, there is a finite index normal subgroup
![]() $\Delta^{\prime}_i \subseteq \Delta_i$
which intersects
$\Delta^{\prime}_i \subseteq \Delta_i$
which intersects
![]() $\ker\!(f)$
exactly in
$\ker\!(f)$
exactly in
![]() $K_i$
and thus the profinite completion of
$K_i$
and thus the profinite completion of
![]() $\Delta^{\prime}_i$
is isomorphic to the profinite completion of
$\Delta^{\prime}_i$
is isomorphic to the profinite completion of
![]() $f\!\left(\Delta^{\prime}_i\right)$
which is a finite index normal subgroup of
$f\!\left(\Delta^{\prime}_i\right)$
which is a finite index normal subgroup of
![]() $\Gamma_i$
. Therefore
$\Gamma_i$
. Therefore
![]() $\Delta^{\prime}_1$
,
$\Delta^{\prime}_1$
,
![]() $\Delta^{\prime}_2$
are profinitely commensurable. However, these groups are not commensurable, since every isomorphism between finite index subgroups maps the completion kernel
$\Delta^{\prime}_2$
are profinitely commensurable. However, these groups are not commensurable, since every isomorphism between finite index subgroups maps the completion kernel
![]() $K_1$
to the kernel
$K_1$
to the kernel
![]() $K_2$
, i.e., it induces an isomorphism of finite index subgroups of
$K_2$
, i.e., it induces an isomorphism of finite index subgroups of
![]() $\Gamma_1$
and
$\Gamma_1$
and
![]() $\Gamma_2$
.
$\Gamma_2$
.
Since
![]() $\Gamma_1, \Gamma_2$
are residually finite and
$\Gamma_1, \Gamma_2$
are residually finite and
![]() $\ker\!(g)$
is finite, there are finite index subgroups
$\ker\!(g)$
is finite, there are finite index subgroups
![]() $\Gamma^{\prime}_1, \Gamma^{\prime}_2$
which do not intersect
$\Gamma^{\prime}_1, \Gamma^{\prime}_2$
which do not intersect
![]() $\ker\!(g)$
so that they are isomorphic to lattices in
$\ker\!(g)$
so that they are isomorphic to lattices in
![]() $G_0$
. As finite index subgroups of
$G_0$
. As finite index subgroups of
![]() $\Gamma_1,\Gamma_2$
they are still profinitely commensurable but not commensurable.
$\Gamma_1,\Gamma_2$
they are still profinitely commensurable but not commensurable.
2·4. The congruence subgroup property and its consequences
A key ingredient in the proof is the congruence subgroup property (CSP): the statement that the kernel
![]() $C(k, \textbf{G})$
of the canonical homomorphism
$C(k, \textbf{G})$
of the canonical homomorphism
![]() $\widehat{\textbf{G}(k)} \rightarrow \overline{\textbf{G}(k)}$
from the arithmetic completion to the congruence completion of the k-rational points of certain k-groups
$\widehat{\textbf{G}(k)} \rightarrow \overline{\textbf{G}(k)}$
from the arithmetic completion to the congruence completion of the k-rational points of certain k-groups
![]() $\textbf{G}$
is finite. We will apply various special cases in which the congruence subgroup property is known to hold true.
$\textbf{G}$
is finite. We will apply various special cases in which the congruence subgroup property is known to hold true.
Theorem 2·4. Let
![]() ${\textbf{G}}$
be a simply connected absolutely almost simple linear algebraic k-group which either is k-isotropic or has type:
${\textbf{G}}$
be a simply connected absolutely almost simple linear algebraic k-group which either is k-isotropic or has type:
-
(i)
 $B_l \ (l \ge 2)$
;
$B_l \ (l \ge 2)$
; -
(ii)
 $C_l \ (l \ge 2)$
$C_l \ (l \ge 2)$
-
(iii)
 $D_l\ (l \ge 5)$
$D_l\ (l \ge 5)$
-
(iv)
 $E_7, E_8, F_4, G_2$
,
$E_7, E_8, F_4, G_2$
,
or let
![]() ${\textbf{G}}$
be the type
${\textbf{G}}$
be the type
![]() ${}^2 A_{m-1}$
group
${}^2 A_{m-1}$
group
![]() ${\textbf{G}} = {\textbf{SU}}_{{\textbf{m}}}(K,h)$
where h is a nondegenerate m-dimensional Hermitian form over a quadratic extension
${\textbf{G}} = {\textbf{SU}}_{{\textbf{m}}}(K,h)$
where h is a nondegenerate m-dimensional Hermitian form over a quadratic extension
![]() $K/k$
with
$K/k$
with
![]() $m \ge 3$
. Assume moreover that
$m \ge 3$
. Assume moreover that
![]() $\sum_{v \in V_\infty(k)} \text{rank}_{k_v} \!{{\textbf{G}}} \ge 2$
and that k is not totally imaginary. Then the congruence kernel
$\sum_{v \in V_\infty(k)} \text{rank}_{k_v} \!{{\textbf{G}}} \ge 2$
and that k is not totally imaginary. Then the congruence kernel
![]() $C(k,{{\textbf{G}}})$
has order at most two. If
$C(k,{{\textbf{G}}})$
has order at most two. If
![]() ${{\textbf{G}}}$
is not topologically simply connected at some real place of k, then
${{\textbf{G}}}$
is not topologically simply connected at some real place of k, then
![]() $C(k, {{\textbf{G}}})$
is trivial.
$C(k, {{\textbf{G}}})$
is trivial.
The theorem is the essence of decades of research on the congruence subgroup problem. References are [ Reference Gille8 ; 21, theorem 9·1, p. 512, theorem 9·5, p. 513, corollary 9·7, p. 515, theorems 9·23 and 9·24; 22, main theorem]. A survey article providing extensive information on CSP can be found in [ Reference Prasad and Rapinchuk23 ]. The following result is another main tool for us.
Theorem 2·5. Let k be an algebraic number field and let
![]() ${{\textbf{G}}}$
be a simply connected simple linear algebraic group over k. Let
${{\textbf{G}}}$
be a simply connected simple linear algebraic group over k. Let
![]() $\Gamma \subseteq {{\textbf{G}}}(k)$
be an arithmetic subgroup. Assume that
$\Gamma \subseteq {{\textbf{G}}}(k)$
be an arithmetic subgroup. Assume that
![]() $G_\infty = \prod_{v \in V_\infty(k)} {{\textbf{G}}}(k_v)$
is not compact.
$G_\infty = \prod_{v \in V_\infty(k)} {{\textbf{G}}}(k_v)$
is not compact.
-
(a)
 $\Gamma \subseteq G_\infty$
is a lattice. If
$\Gamma \subseteq G_\infty$
is a lattice. If
 ${{\textbf{G}}}(k_v)$
is compact for some
${{\textbf{G}}}(k_v)$
is compact for some
 $v \in V_\infty(k)$
, then
$v \in V_\infty(k)$
, then
 $\Gamma$
is cocompact.
$\Gamma$
is cocompact. -
(b) Assume that
 ${{\textbf{G}}}$
has CSP. Then the profinite completion
${{\textbf{G}}}$
has CSP. Then the profinite completion
 $\widehat{\Gamma}$
is commensurable with the open compact subgroups of
$\widehat{\Gamma}$
is commensurable with the open compact subgroups of
 ${{\textbf{G}}}\!\left(\mathbb{A}_k^f\right)$
.
${{\textbf{G}}}\!\left(\mathbb{A}_k^f\right)$
.
Proof. Part (a) is a famous result of Borel and Harish-Chandra [
Reference Borel and Chandra3
]. To prove part (b), note that by CSP, the kernel of the map
![]() $\varphi\colon \widehat{\Gamma} \to \textbf{G}\!\left(\mathbb{A}_k^f\right)$
is finite. Passing to a finite index subgroup of
$\varphi\colon \widehat{\Gamma} \to \textbf{G}\!\left(\mathbb{A}_k^f\right)$
is finite. Passing to a finite index subgroup of
![]() $\Gamma$
, we can assume that
$\Gamma$
, we can assume that
![]() $\varphi$
is injective. The strong approximation theorem holds since
$\varphi$
is injective. The strong approximation theorem holds since
![]() $\textbf{G}$
is simply connected [
Reference Platonov and Rapinchuk21
, theorem 7·12] and implies that the image of
$\textbf{G}$
is simply connected [
Reference Platonov and Rapinchuk21
, theorem 7·12] and implies that the image of
![]() $\varphi$
is open (and compact since
$\varphi$
is open (and compact since
![]() $\widehat{\Gamma}$
is compact).
$\widehat{\Gamma}$
is compact).
Finally, we will need to know that a collection of local isomorphisms of algebraic groups assembles to an adelic isomorphism.
Lemma 2·6. Let k be an algebraic number field and let
![]() ${{\textbf{G}}}$
,
${{\textbf{G}}}$
,
![]() ${{\textbf{H}}}$
be two semi-simple linear algebraic groups over k. If
${{\textbf{H}}}$
be two semi-simple linear algebraic groups over k. If
![]() ${{\textbf{G}}}$
,
${{\textbf{G}}}$
,
![]() ${{\textbf{H}}}$
are isomorphic at all finite places, i.e.,
${{\textbf{H}}}$
are isomorphic at all finite places, i.e.,
![]() ${{\textbf{G}}} \times_k k_v \cong {{\textbf{H}}} \times_k k_v$
for all
${{\textbf{G}}} \times_k k_v \cong {{\textbf{H}}} \times_k k_v$
for all
![]() $v \in V_f(k)$
, then
$v \in V_f(k)$
, then
as topological groups.
Proof. By assumption the topological groups
![]() $\textbf{G}(k_v)$
and
$\textbf{G}(k_v)$
and
![]() $\textbf{H}(k_v)$
are isomorphic at all finite places v of k. We pick models of
$\textbf{H}(k_v)$
are isomorphic at all finite places v of k. We pick models of
![]() $\textbf{G}$
,
$\textbf{G}$
,
![]() $\textbf{H}$
over the ring of integers
$\textbf{H}$
over the ring of integers
![]() $\mathcal{O}_k$
of k. Then for all but finitely many places
$\mathcal{O}_k$
of k. Then for all but finitely many places
![]() $v \in V_f(k)$
, the compact subgroups
$v \in V_f(k)$
, the compact subgroups
![]() $\textbf{G}(\mathcal{O}_{k,v})$
,
$\textbf{G}(\mathcal{O}_{k,v})$
,
![]() $\textbf{H}(\mathcal{O}_{k,v})$
are hyperspecial [
Reference Tits32
, 3·9·1] and hence isomorphic [
Reference Tits32
, 2·5]. We deduce that
$\textbf{H}(\mathcal{O}_{k,v})$
are hyperspecial [
Reference Tits32
, 3·9·1] and hence isomorphic [
Reference Tits32
, 2·5]. We deduce that
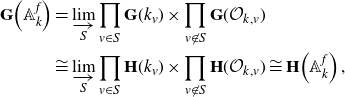 \begin{align*}\textbf{G}\!\left(\mathbb{A}_k^f\right) &= \varinjlim_S \prod_{v \in S} \textbf{G}(k_v) \times \prod_{v \not\in S} \textbf{G}(\mathcal{O}_{k,v}) \\ &\cong \varinjlim_S \prod_{v \in S} \textbf{H}(k_v) \times \prod_{v \not\in S} \textbf{H}(\mathcal{O}_{k,v}) \cong \textbf{H}\!\left(\mathbb{A}_k^f\right),\end{align*}
\begin{align*}\textbf{G}\!\left(\mathbb{A}_k^f\right) &= \varinjlim_S \prod_{v \in S} \textbf{G}(k_v) \times \prod_{v \not\in S} \textbf{G}(\mathcal{O}_{k,v}) \\ &\cong \varinjlim_S \prod_{v \in S} \textbf{H}(k_v) \times \prod_{v \not\in S} \textbf{H}(\mathcal{O}_{k,v}) \cong \textbf{H}\!\left(\mathbb{A}_k^f\right),\end{align*}
where the direct limit runs over all finite sets S of finite places of k.
2·5. Margulis superrigidity
Margulis superrigidity will be used to show that certain arithmetic lattices are not abstractly commensurable.
Theorem 2·7 (Margulis). Let
![]() $k_1$
,
$k_1$
,
![]() $k_2$
be number fields and let
$k_2$
be number fields and let
![]() ${{\textbf{G}}}_{{\textbf{1}}},{{\textbf{G}}}_{{{\textbf{2}}}}$
be simply connected, absolutely almost simple linear algebraic groups over
${{\textbf{G}}}_{{\textbf{1}}},{{\textbf{G}}}_{{{\textbf{2}}}}$
be simply connected, absolutely almost simple linear algebraic groups over
![]() $k_1$
and
$k_1$
and
![]() $k_2$
respectively. Assume that
$k_2$
respectively. Assume that
![]() $\sum_{v\in V_{\infty}(k_j)} \text{rk}_{k_j}(G_j(k_{j,v})) \geq 2$
for all
$\sum_{v\in V_{\infty}(k_j)} \text{rk}_{k_j}(G_j(k_{j,v})) \geq 2$
for all
![]() $j \in \{1,2\}$
. The arithmetic subgroups
$j \in \{1,2\}$
. The arithmetic subgroups
![]() $\Gamma_1 \subset {{\textbf{G}}}_{{{\textbf{1}}}}(k_1)$
and
$\Gamma_1 \subset {{\textbf{G}}}_{{{\textbf{1}}}}(k_1)$
and
![]() $\Gamma_2 \subset {{\textbf{G}}}_{{{\textbf{2}}}}(k_2)$
are commensurable if and only if there is an isomorphism of fields
$\Gamma_2 \subset {{\textbf{G}}}_{{{\textbf{2}}}}(k_2)$
are commensurable if and only if there is an isomorphism of fields
![]() $\sigma\,:\, k_1 \to k_2$
and a
$\sigma\,:\, k_1 \to k_2$
and a
![]() $k_2$
-isomorphism of algebraic groups
$k_2$
-isomorphism of algebraic groups
![]() $\eta\colon {}^\sigma{{\textbf{G}}}_{{{\textbf{1}}}} \to {{\textbf{G}}}_{{{\textbf{2}}}}$
.
$\eta\colon {}^\sigma{{\textbf{G}}}_{{{\textbf{1}}}} \to {{\textbf{G}}}_{{{\textbf{2}}}}$
.
Proof. After passing to finite index subgroups, we can assume that there exists an isomorphism
![]() $\delta \colon \Gamma_1 \xrightarrow{\cong} \Gamma_2$
. Then by Margulis superrigidity [
Reference Margulis18
, theorem (C), p. 259], there exists
$\delta \colon \Gamma_1 \xrightarrow{\cong} \Gamma_2$
. Then by Margulis superrigidity [
Reference Margulis18
, theorem (C), p. 259], there exists
![]() $\sigma \colon k_1 \to k_2$
and an epimorphism
$\sigma \colon k_1 \to k_2$
and an epimorphism
![]() $\eta \colon {}^\sigma \textbf{G}_{\textbf{1}} \rightarrow \textbf{G}_{\textbf{2}}$
such that
$\eta \colon {}^\sigma \textbf{G}_{\textbf{1}} \rightarrow \textbf{G}_{\textbf{2}}$
such that
![]() $\delta$
agrees with
$\delta$
agrees with
![]() $\eta$
on a finite index subgroup of
$\eta$
on a finite index subgroup of
![]() $\Gamma_1$
. Without loss of generality
$\Gamma_1$
. Without loss of generality
![]() $\delta = \eta|_{\Gamma_1}$
. The same argument applied to
$\delta = \eta|_{\Gamma_1}$
. The same argument applied to
![]() $\delta^{-1}$
implies that
$\delta^{-1}$
implies that
![]() $\sigma$
is an isomorphism and further (since
$\sigma$
is an isomorphism and further (since
![]() $\textbf{G}_{\textbf{2}}$
is simply connected) that
$\textbf{G}_{\textbf{2}}$
is simply connected) that
![]() $\eta$
is an isomorphism.
$\eta$
is an isomorphism.
Conversely, if
![]() $\sigma$
and
$\sigma$
and
![]() $\eta$
exist, then
$\eta$
exist, then
![]() $\Gamma_1$
and
$\Gamma_1$
and
![]() $\Gamma_2$
are (isomorphic to) arithmetic subgroups of the same algebraic group and are thus commensurable.
$\Gamma_2$
are (isomorphic to) arithmetic subgroups of the same algebraic group and are thus commensurable.
3. Proof of Theorem 1·1
In this section, k denotes a number field with
![]() $n : = [k \,:\, \mathbb{Q}] > 2$
and with trivial automorphism group. We will say k has type I if it is totally real; see Lemma 2·1. In this case
$n : = [k \,:\, \mathbb{Q}] > 2$
and with trivial automorphism group. We will say k has type I if it is totally real; see Lemma 2·1. In this case
![]() $k_1, \dots, k_n$
denote the completions of k at the archimedean places. We will say k has type II if it has exactly one complex place; see Lemma 2·2. In this case
$k_1, \dots, k_n$
denote the completions of k at the archimedean places. We will say k has type II if it has exactly one complex place; see Lemma 2·2. In this case
![]() $k_1, \dots, k_{n-1}$
denote the completions at the archimedean places of k with
$k_1, \dots, k_{n-1}$
denote the completions at the archimedean places of k with
![]() $k_1 \cong \mathbb{C}$
.
$k_1 \cong \mathbb{C}$
.
3·1. Reduction to
 $G = \textbf{G}(\mathbb{R})$
or
$G = \textbf{G}(\mathbb{R})$
or
 $G = \textbf{G}(\mathbb{C})$
$G = \textbf{G}(\mathbb{C})$
As a first step of the proof of Theorem 1·1, we observe that we may assume that the Lie group G is the group of real or complex points of a simply connected simple algebraic group. To this end, let G be a connected simple Lie group with finite center. Let
![]() $\mathfrak{g}$
be the Lie algebra of G. Since the center Z(G) of G is finite and the adjoint group
$\mathfrak{g}$
be the Lie algebra of G. Since the center Z(G) of G is finite and the adjoint group
![]() $G/Z(G)$
, being a subgroup of
$G/Z(G)$
, being a subgroup of
![]() $\textrm{Aut}(\mathfrak{g})$
, is linear, we may assume by Lemma 2·3 that G has trivial center.
$\textrm{Aut}(\mathfrak{g})$
, is linear, we may assume by Lemma 2·3 that G has trivial center.
If
![]() $\mathfrak{g} \otimes_\mathbb{R} \mathbb{C}$
is simple, then the linear algebraic
$\mathfrak{g} \otimes_\mathbb{R} \mathbb{C}$
is simple, then the linear algebraic
![]() $\mathbb{R}$
-group
$\mathbb{R}$
-group
![]() $\textbf{G}_{\text{ad}} = \textrm{Aut}_\mathbb{R}(\mathfrak{g})$
is absolutely simple and satisfies
$\textbf{G}_{\text{ad}} = \textrm{Aut}_\mathbb{R}(\mathfrak{g})$
is absolutely simple and satisfies
![]() $\textbf{G}_{\text{ad}}(\mathbb{R})^0 = G$
. Let
$\textbf{G}_{\text{ad}}(\mathbb{R})^0 = G$
. Let
![]() $\textbf{G}$
be the simply connected covering of
$\textbf{G}$
be the simply connected covering of
![]() $\textbf{G}_{\text{ad}}$
. By Lemma 2·3 it is sufficient to show for every n that
$\textbf{G}_{\text{ad}}$
. By Lemma 2·3 it is sufficient to show for every n that
![]() $\textbf{G}(\mathbb{R})$
has n profinitely isomorphic lattices which are not commensurable.
$\textbf{G}(\mathbb{R})$
has n profinitely isomorphic lattices which are not commensurable.
If
![]() $\mathfrak{g} \otimes_\mathbb{R} \mathbb{C}$
is not simple, then
$\mathfrak{g} \otimes_\mathbb{R} \mathbb{C}$
is not simple, then
![]() $\mathfrak{g}$
possesses a complex structure which turns it into a simple Lie algebra over
$\mathfrak{g}$
possesses a complex structure which turns it into a simple Lie algebra over
![]() $\mathbb{C}$
. For any such structure, the
$\mathbb{C}$
. For any such structure, the
![]() $\mathbb{C}$
-group
$\mathbb{C}$
-group
![]() $\textbf{G}_{\text{ad}} = \textrm{Aut}_\mathbb{C}(\mathfrak{g})$
is (absolutely) simple and satisfies
$\textbf{G}_{\text{ad}} = \textrm{Aut}_\mathbb{C}(\mathfrak{g})$
is (absolutely) simple and satisfies
![]() $\textbf{G}_{\text{ad}}(\mathbb{C}) = G$
. Again
$\textbf{G}_{\text{ad}}(\mathbb{C}) = G$
. Again
![]() $\textbf{G}$
will denote the simply connected covering group of
$\textbf{G}$
will denote the simply connected covering group of
![]() $\textbf{G}_{\text{ad}}$
and it is enough to find n non-commensurable profinitely isomorphic lattices in
$\textbf{G}_{\text{ad}}$
and it is enough to find n non-commensurable profinitely isomorphic lattices in
![]() $\textbf{G}(\mathbb{C})$
.
$\textbf{G}(\mathbb{C})$
.
With these remarks, we associated to each local isomorphism class of Lie groups G as in Theorem 1·1 a connected simply connected absolutely almost simple linear algebraic
![]() $\mathbb{K}$
-group
$\mathbb{K}$
-group
![]() $\textbf{G}$
with
$\textbf{G}$
with
![]() $\mathbb{K} = \mathbb{R}$
or
$\mathbb{K} = \mathbb{R}$
or
![]() $\mathbb{C}$
which is unique up to
$\mathbb{C}$
which is unique up to
![]() $\mathbb{K}$
-isomorphism. Our task now is to find n profinitely commensurable lattices in
$\mathbb{K}$
-isomorphism. Our task now is to find n profinitely commensurable lattices in
![]() $\textbf{G}(\mathbb{K})$
which are not commensurable. The common intersection of the profinite completions then corresponds to non-commensurable lattices which are profinitely isomorphic, see [
Reference Ribes and Zalesskii27
, proposition 3·2·2, p. 80] and, for instance, [
Reference Kammeyer10
, proposition 6·39, p. 159].
$\textbf{G}(\mathbb{K})$
which are not commensurable. The common intersection of the profinite completions then corresponds to non-commensurable lattices which are profinitely isomorphic, see [
Reference Ribes and Zalesskii27
, proposition 3·2·2, p. 80] and, for instance, [
Reference Kammeyer10
, proposition 6·39, p. 159].
3·2. Overview of the proof
Let us first assume that
![]() $\mathbb{K} = \mathbb{R}$
, in which case we take k of type I. The general idea of the proof in this case was already outlined in the introduction. At this point we have to point out, however, that the argument only goes through provided the following two requirements are met.
$\mathbb{K} = \mathbb{R}$
, in which case we take k of type I. The general idea of the proof in this case was already outlined in the introduction. At this point we have to point out, however, that the argument only goes through provided the following two requirements are met.
-
(i) We need to assume that
 $\textbf{G}$
and the
$\textbf{G}$
and the
 $\mathbb{R}$
-anisotropic real form
$\mathbb{R}$
-anisotropic real form
 $\textbf{G}^{u}$
with
$\textbf{G}^{u}$
with
 $\textbf{G} \times_\mathbb{R} \mathbb{C} \cong_\mathbb{C} \textbf{G}^u \times_\mathbb{R} \mathbb{C}$
are inner forms of each other. This is automatic unless the Dynkin diagram has symmetries, meaning
$\textbf{G} \times_\mathbb{R} \mathbb{C} \cong_\mathbb{C} \textbf{G}^u \times_\mathbb{R} \mathbb{C}$
are inner forms of each other. This is automatic unless the Dynkin diagram has symmetries, meaning
 $\textbf{G}$
has type
$\textbf{G}$
has type
 $A_m$
,
$A_m$
,
 $D_m$
, or
$D_m$
, or
 $E_6$
. In these cases, one can read off from the Tits indices [
Reference Tits31
, table II], whether the condition is satisfied: In type
$E_6$
. In these cases, one can read off from the Tits indices [
Reference Tits31
, table II], whether the condition is satisfied: In type
 $A_m$
, the condition fails for
$A_m$
, the condition fails for
 $\textrm{SL}_{m+1}(\mathbb{R})$
and
$\textrm{SL}_{m+1}(\mathbb{R})$
and
 $\textrm{SL}_{m+1}(\mathbb{H})$
, while the groups
$\textrm{SL}_{m+1}(\mathbb{H})$
, while the groups
 $\textrm{SU}(r,s)$
with
$\textrm{SU}(r,s)$
with
 $r+s = m+1$
satisfy this requirement. In type
$r+s = m+1$
satisfy this requirement. In type
 $D_m$
, the groups
$D_m$
, the groups
 $\textrm{SO}^*(2m) = \textrm{SO}(m, \mathbb{H})$
are inner twists of the compact form
$\textrm{SO}^*(2m) = \textrm{SO}(m, \mathbb{H})$
are inner twists of the compact form
 $\textrm{SO}(2m)$
. For the groups
$\textrm{SO}(2m)$
. For the groups
 $\textrm{SO}^0(r,s)$
with
$\textrm{SO}^0(r,s)$
with
 $r+s = 2m$
, the condition is satisfied if r and s are even and fails if r and s are odd. Finally, in type
$r+s = 2m$
, the condition is satisfied if r and s are even and fails if r and s are odd. Finally, in type
 $E_6$
, the condition is satisfied for
$E_6$
, the condition is satisfied for
 $E_{6(2)}$
and
$E_{6(2)}$
and
 $E_{6({-}14)}$
and fails for
$E_{6({-}14)}$
and fails for
 $E_{6(6)}$
and
$E_{6(6)}$
and
 $E_{6({-}26)}$
.
$E_{6({-}26)}$
. -
(ii) We need that k-anisotropic forms of
 $\textbf{G}$
defined over k satisfy the congruence subgroup property. This is still generally open in type
$\textbf{G}$
defined over k satisfy the congruence subgroup property. This is still generally open in type
 $A_m$
,
$A_m$
,
 $D_4$
and
$D_4$
and
 $E_6$
.
$E_6$
.
Property (ii) forces us to exclude type
![]() $E_6$
altogether. In type
$E_6$
altogether. In type
![]() $A_m$
, however, CSP is known for special unitary groups
$A_m$
, however, CSP is known for special unitary groups
![]() $\textbf{SU}(K/k,h)$
of hermitian forms h over a quadratic field extension
$\textbf{SU}(K/k,h)$
of hermitian forms h over a quadratic field extension
![]() $K/k$
as we stated in Theorem 2·4. This allows us to prove Theorem 1·1 for the groups
$K/k$
as we stated in Theorem 2·4. This allows us to prove Theorem 1·1 for the groups
![]() $\textrm{SU}(r,s)$
in Section 3·3. There we also present a workaround that allows us to include the groups
$\textrm{SU}(r,s)$
in Section 3·3. There we also present a workaround that allows us to include the groups
![]() $\textrm{SL}_{2m}(\mathbb{R})$
in spite of the failure of property (i).
$\textrm{SL}_{2m}(\mathbb{R})$
in spite of the failure of property (i).
Similarly, Kneser [
Reference Kneser14
] has shown that CSP holds for spinor groups. Using this, we can construct the required non-commensurable but profinitely isomorphic lattices in all the real forms
![]() $\textrm{SO}^0(6,2)$
,
$\textrm{SO}^0(6,2)$
,
![]() $\textrm{SO}^0(5,3)$
,
$\textrm{SO}^0(5,3)$
,
![]() $\textrm{SO}^0(4,4)$
, and
$\textrm{SO}^0(4,4)$
, and
![]() $\textrm{SO}^*(8)$
of type
$\textrm{SO}^*(8)$
of type
![]() $D_4$
as arithmetic spinor groups. So it is no issue for us that CSP is still open for anisotropic type
$D_4$
as arithmetic spinor groups. So it is no issue for us that CSP is still open for anisotropic type
![]() ${}^{3,6}D_4$
forms (whose unique inner quasi-split twist has a splitting field extension of degree 3 or 6, so called triality forms). Note also that property (i) fails in some
${}^{3,6}D_4$
forms (whose unique inner quasi-split twist has a splitting field extension of degree 3 or 6, so called triality forms). Note also that property (i) fails in some
![]() $D_m$
cases with
$D_m$
cases with
![]() $m \ge 4$
. Therefore, we will sort out the type
$m \ge 4$
. Therefore, we will sort out the type
![]() $D_m$
groups with
$D_m$
groups with
![]() $m \ge 4$
separately in Section 3·4.
$m \ge 4$
separately in Section 3·4.
With the special cases taken care of, we treat the remaining
![]() $\mathbb{R}$
-groups of type
$\mathbb{R}$
-groups of type
![]() $B_m$
,
$B_m$
,
![]() $C_m$
,
$C_m$
,
![]() $E_7$
,
$E_7$
,
![]() $E_8$
,
$E_8$
,
![]() $F_4$
, and
$F_4$
, and
![]() $G_2$
in Section 3·5. For all these, the general strategy applies because (i) and (ii) are satisfied.
$G_2$
in Section 3·5. For all these, the general strategy applies because (i) and (ii) are satisfied.
Finally, we give the proof of Theorem 1·1 for
![]() $\mathbb{K} = \mathbb{C}$
and
$\mathbb{K} = \mathbb{C}$
and
![]() $\textbf{G}$
of type
$\textbf{G}$
of type
![]() $B_m$
,
$B_m$
,
![]() $C_m$
,
$C_m$
,
![]() $D_m$
with
$D_m$
with
![]() $m \ge 5$
, and
$m \ge 5$
, and
![]() $E_7$
in Section 3·6. Also in the complex case, type
$E_7$
in Section 3·6. Also in the complex case, type
![]() $A_m$
and
$A_m$
and
![]() $D_4$
need special attention because of the incomplete status of CSP. The type
$D_4$
need special attention because of the incomplete status of CSP. The type
![]() $D_4$
group
$D_4$
group
![]() $\textrm{SO}_8(\mathbb{C})$
can again be covered by Kneser’s result so that it was more convenient to include it in Section 3·4. A similar trick as for
$\textrm{SO}_8(\mathbb{C})$
can again be covered by Kneser’s result so that it was more convenient to include it in Section 3·4. A similar trick as for
![]() $\textrm{SL}_{2m}(\mathbb{R})$
also allows us to cover the type
$\textrm{SL}_{2m}(\mathbb{R})$
also allows us to cover the type
![]() $A_{2m-1}$
group
$A_{2m-1}$
group
![]() $\textrm{SL}_{2m}(\mathbb{C})$
. This argument is included in Section 3·3.
$\textrm{SL}_{2m}(\mathbb{C})$
. This argument is included in Section 3·3.
3·3. Type
 $A_\bullet:$
$A_\bullet:$
 $\text{SU}(r,s)$
,
$\text{SU}(r,s)$
,
 $\text{SL}_{2m}(\mathbb{R})$
and
$\text{SL}_{2m}(\mathbb{R})$
and
 $\text{SL}_{2m}(\mathbb{C})$
$\text{SL}_{2m}(\mathbb{C})$
As a first instance we consider the case when G is either of the groups
![]() $\textrm{SU}(r,s)$
with
$\textrm{SU}(r,s)$
with
![]() $r,s \geq 2$
,
$r,s \geq 2$
,
![]() $\textrm{SL}_{2m}(\mathbb{R})$
and
$\textrm{SL}_{2m}(\mathbb{R})$
and
![]() $\textrm{SL}_{2m}(\mathbb{C})$
with
$\textrm{SL}_{2m}(\mathbb{C})$
with
![]() $m \geq 2$
. In these concrete examples it is instructive how local-global principles are key to our investigation.
$m \geq 2$
. In these concrete examples it is instructive how local-global principles are key to our investigation.
It is wellknown that hermitian forms for the extension
![]() $\mathbb{C}/\mathbb{R}$
are classified by dimension and signature. We also recall that hermitian forms for a quadratic extension
$\mathbb{C}/\mathbb{R}$
are classified by dimension and signature. We also recall that hermitian forms for a quadratic extension
![]() $E/F$
of p-adic fields are classified by dimension and discriminant
$E/F$
of p-adic fields are classified by dimension and discriminant
![]() $d \in \{\pm 1\}$
(i.e,
$d \in \{\pm 1\}$
(i.e,
![]() $d=1$
exactly if the determinant lies in the image of the norm
$d=1$
exactly if the determinant lies in the image of the norm
![]() $\textrm{N}_{E/F} \colon E^\times\to F^\times$
); see e.g. [
Reference Jacobowitz9
, theorem 3·1].
$\textrm{N}_{E/F} \colon E^\times\to F^\times$
); see e.g. [
Reference Jacobowitz9
, theorem 3·1].
Fix a dimension
![]() $m \geq 2$
. Suppose that
$m \geq 2$
. Suppose that
![]() $K= k(\sqrt{a})$
is a quadratic extension of k. Let
$K= k(\sqrt{a})$
is a quadratic extension of k. Let
![]() $V_{\infty}^{K}(k)$
denote the set of non-split archimedean places of k, i.e., the set of real places v where a is negative with respect to the embedding
$V_{\infty}^{K}(k)$
denote the set of non-split archimedean places of k, i.e., the set of real places v where a is negative with respect to the embedding
![]() $k \to k_v$
. We will use the following result of Landherr [
Reference Landherr16
] on the existence of hermitian forms with prescribed local properties: Choosing a pair of nonnegative integers
$k \to k_v$
. We will use the following result of Landherr [
Reference Landherr16
] on the existence of hermitian forms with prescribed local properties: Choosing a pair of nonnegative integers
![]() $(r_i, s_i)$
with
$(r_i, s_i)$
with
![]() $r_i + s_i = m$
for each
$r_i + s_i = m$
for each
![]() $v_i \in V^K_\infty(k)$
and choosing
$v_i \in V^K_\infty(k)$
and choosing
![]() $d_v \in \{\pm1\}$
for each
$d_v \in \{\pm1\}$
for each
![]() $v \in V_f(k)$
, there exists a
$v \in V_f(k)$
, there exists a
![]() $K/k$
-hermitian form of dimension m with signature
$K/k$
-hermitian form of dimension m with signature
![]() $(r_i,s_i)$
at
$(r_i,s_i)$
at
![]() $v_i \in V_{\infty}^{K}(k)$
and discriminant
$v_i \in V_{\infty}^{K}(k)$
and discriminant
![]() $d_v \in \{\pm 1\}$
at
$d_v \in \{\pm 1\}$
at
![]() $v \in V_f(k)$
if and only if:
$v \in V_f(k)$
if and only if:
-
(i)
 $d_v = 1$
for almost all
$d_v = 1$
for almost all
 $v \in V_f(k)$
;
$v \in V_f(k)$
; -
(ii)
 $d_v = 1$
whenever v splits in K; and
$d_v = 1$
whenever v splits in K; and -
(iii)
 $\prod_{v_i \in V_{\infty}^{\text{K}}(k)} ({-}1)^{s_i} \prod_{v \in V_f(k)} d_v = 1.$
$\prod_{v_i \in V_{\infty}^{\text{K}}(k)} ({-}1)^{s_i} \prod_{v \in V_f(k)} d_v = 1.$
The hermitian form is uniquely determined by this data.
3·3·1.
 $\text{SU}(r,s)$
with
$\text{SU}(r,s)$
with
 $r,s \geq 2$
$r,s \geq 2$
We take k of type I and fix some
![]() $w^0 \in V_f(k)$
. By weak approximation, there is an element
$w^0 \in V_f(k)$
. By weak approximation, there is an element
![]() $a \in k^\times$
which is negative at all real places and is a non-square in
$a \in k^\times$
which is negative at all real places and is a non-square in
![]() $k_{w^0}$
. Define
$k_{w^0}$
. Define
![]() $K = k(\sqrt{a})$
and observe that by construction all archimedean places are non-split. In addition, the finite place
$K = k(\sqrt{a})$
and observe that by construction all archimedean places are non-split. In addition, the finite place
![]() $w^0$
does not split in K. Using the result of Landherr, there is a unique hermitian form
$w^0$
does not split in K. Using the result of Landherr, there is a unique hermitian form
![]() $h_j$
such that:
$h_j$
such that:
-
(i) the signature at the jth real place is (r, s);
-
(ii) the signature at all other real places is
 $(r+s,0)$
;
$(r+s,0)$
; -
(iii) the discriminant at
 $w^0$
is
$w^0$
is
 $d_{w^0} = ({-}1)^s$
; and
$d_{w^0} = ({-}1)^s$
; and -
(iv) the discriminant is
 $d_v = 1$
for every
$d_v = 1$
for every
 $v \in V_f(k)\setminus\{w^0\}$
.
$v \in V_f(k)\setminus\{w^0\}$
.
These hermitian forms define linear algebraic groups
![]() $\textbf{SU}(h_j) $
over k and by Theorem 2·5 (a) arithmetic subgroups
$\textbf{SU}(h_j) $
over k and by Theorem 2·5 (a) arithmetic subgroups
![]() $\Gamma_j \subset \textbf{SU}(h_j)(k)$
which are cocompact lattices in
$\Gamma_j \subset \textbf{SU}(h_j)(k)$
which are cocompact lattices in
![]() $\textbf{SU}(h_j)(k_j) = \textrm{SU}(r,s)$
. These lattices have a congruence kernel of order at most two by Theorem 2·4 (Since the compact Lie group
$\textbf{SU}(h_j)(k_j) = \textrm{SU}(r,s)$
. These lattices have a congruence kernel of order at most two by Theorem 2·4 (Since the compact Lie group
![]() $\textbf{SU}(r+s)$
is topologically simply connected, the congruence kernel might however be nontrivial.) In any case, hermitian forms over p-adic fields are classified by dimension and discriminant [
Reference Jacobowitz9
, theorem 3·1], so the forms
$\textbf{SU}(r+s)$
is topologically simply connected, the congruence kernel might however be nontrivial.) In any case, hermitian forms over p-adic fields are classified by dimension and discriminant [
Reference Jacobowitz9
, theorem 3·1], so the forms
![]() $h_j$
are isometric at each finite place. By Lemma 2·6 the groups
$h_j$
are isometric at each finite place. By Lemma 2·6 the groups
![]() $\textbf{SU}(h_j)\!\left(\mathbb{A}_k^f\right)$
are all isomorphic. It follows immediately from Theorem 2·5 (b) that
$\textbf{SU}(h_j)\!\left(\mathbb{A}_k^f\right)$
are all isomorphic. It follows immediately from Theorem 2·5 (b) that
![]() $\Gamma_i$
and
$\Gamma_i$
and
![]() $\Gamma_j$
are pairwise profinitely commensurable. Finally, we observe that the groups
$\Gamma_j$
are pairwise profinitely commensurable. Finally, we observe that the groups
![]() $\textbf{SU}(h_j)$
are not isomorphic. By construction k has no non-trivial automorphisms and therefore superrigidity via Theorem 2·7 (we recall that
$\textbf{SU}(h_j)$
are not isomorphic. By construction k has no non-trivial automorphisms and therefore superrigidity via Theorem 2·7 (we recall that
![]() $r,s \geq 2$
) implies that
$r,s \geq 2$
) implies that
![]() $\Gamma_i$
and
$\Gamma_i$
and
![]() $\Gamma_j$
are not commensurable for
$\Gamma_j$
are not commensurable for
![]() $i \neq j$
.
$i \neq j$
.
3·3·2.
 $\text{SL}_{2m}(\mathbb{R})$
and
$\text{SL}_{2m}(\mathbb{R})$
and
 $\text{SL}_{2m}(\mathbb{C})$
for
$\text{SL}_{2m}(\mathbb{C})$
for
 $m \geq 2$
$m \geq 2$
Let
![]() $\mathbb{K}$
denote either
$\mathbb{K}$
denote either
![]() $\mathbb{R}$
or
$\mathbb{R}$
or
![]() $\mathbb{C}$
and let
$\mathbb{C}$
and let
![]() $G = \textrm{SL}_{2m}(\mathbb{K})$
. If
$G = \textrm{SL}_{2m}(\mathbb{K})$
. If
![]() $\mathbb{K} = \mathbb{R}$
we take k of type I and otherwise of type II. Pick a rational prime number p which splits completely in k and let
$\mathbb{K} = \mathbb{R}$
we take k of type I and otherwise of type II. Pick a rational prime number p which splits completely in k and let
![]() $w_1,\dots, w_n$
denote the places of k dividing p, i.e.,
$w_1,\dots, w_n$
denote the places of k dividing p, i.e.,
![]() $k_{w_i} \cong \mathbb{Q}_p$
. We fix an additional finite place
$k_{w_i} \cong \mathbb{Q}_p$
. We fix an additional finite place
![]() $w^0 \in V_f(k)$
which is distinct from
$w^0 \in V_f(k)$
which is distinct from
![]() $w_1,\dots,w_n$
. By weak approximation, there is an element
$w_1,\dots,w_n$
. By weak approximation, there is an element
![]() $a \in k^\times$
which satisfies: a is negative in
$a \in k^\times$
which satisfies: a is negative in
![]() $k_i$
for all
$k_i$
for all
![]() $i\geq 2$
, represents a prescribed non-square element
$i\geq 2$
, represents a prescribed non-square element
![]() $x \in \mathbb{Q}^{\times}_p$
modulo squares at the places
$x \in \mathbb{Q}^{\times}_p$
modulo squares at the places
![]() $w_1, \dots, w_n$
and is a non-square at
$w_1, \dots, w_n$
and is a non-square at
![]() $w^0$
. If
$w^0$
. If
![]() $\mathbb{K} = \mathbb{R}$
we can arrange that, in addition, a is positive in
$\mathbb{K} = \mathbb{R}$
we can arrange that, in addition, a is positive in
![]() $k_1$
. Define
$k_1$
. Define
![]() $K = k(\sqrt{a})$
. Then
$K = k(\sqrt{a})$
. Then
![]() $V_\infty^K(k)$
contains all but the first archimedean places. By construction, the places
$V_\infty^K(k)$
contains all but the first archimedean places. By construction, the places
![]() $w_1,\dots, w_n, w^0$
are not split in K and the quadratic extensions
$w_1,\dots, w_n, w^0$
are not split in K and the quadratic extensions
![]() $K_{w_i}/k_{w_i}$
are isomorphic to
$K_{w_i}/k_{w_i}$
are isomorphic to
![]() $\mathbb{Q}_p(\sqrt{x})/\mathbb{Q}_p$
. Using the result of Landherr, there is a unique hermitian form
$\mathbb{Q}_p(\sqrt{x})/\mathbb{Q}_p$
. Using the result of Landherr, there is a unique hermitian form
![]() $h_j$
such that:
$h_j$
such that:
-
(i) the signature at
 $k_2,\dots,k_n$
is (2m, 0);
$k_2,\dots,k_n$
is (2m, 0); -
(ii) the discriminant at
 $w^0$
and
$w^0$
and
 $w_j$
equals
$w_j$
equals
 $-1$
; and
$-1$
; and -
(iii) the discriminant is
 $d_v = 1$
for every
$d_v = 1$
for every
 $v \in V_f(k) \setminus\{w_j,w^0\}$
.
$v \in V_f(k) \setminus\{w_j,w^0\}$
.
By construction,
![]() $\textbf{SU}(h_j)(k_i) \cong \textrm{SU}(2m)$
for all
$\textbf{SU}(h_j)(k_i) \cong \textrm{SU}(2m)$
for all
![]() $i \geq 2$
. We observe that
$i \geq 2$
. We observe that
![]() $\textbf{SU}(h_j)(k_1) \cong \textrm{SL}_{2m}(\mathbb{K})$
due to the choices of k and a. The groups
$\textbf{SU}(h_j)(k_1) \cong \textrm{SL}_{2m}(\mathbb{K})$
due to the choices of k and a. The groups
![]() $\textbf{SU}(h_j)$
are pairwise non-isomorphic, since they are non-isomorphic at one of the finite places
$\textbf{SU}(h_j)$
are pairwise non-isomorphic, since they are non-isomorphic at one of the finite places
![]() $w_1,\dots, w_n$
. Here it is essential that 2m is even; only under this assumption the classification [
Reference Tits32
, 4·4] entails that non-isomorphic hermitian forms have non-isomorphic special unitary groups. We claim that the topological groups
$w_1,\dots, w_n$
. Here it is essential that 2m is even; only under this assumption the classification [
Reference Tits32
, 4·4] entails that non-isomorphic hermitian forms have non-isomorphic special unitary groups. We claim that the topological groups
![]() $\textbf{SU}(h_j)\left(\mathbb{A}^f_k\right) \cong \textbf{SU}(h_i)\!\left(\mathbb{A}_k^f\right)$
are isomorphic for all i, j. Indeed, the groups
$\textbf{SU}(h_j)\left(\mathbb{A}^f_k\right) \cong \textbf{SU}(h_i)\!\left(\mathbb{A}_k^f\right)$
are isomorphic for all i, j. Indeed, the groups
![]() $\textbf{SU}(h_j)$
are isomorphic at all finite places except for
$\textbf{SU}(h_j)$
are isomorphic at all finite places except for
![]() $w_1, \dots, w_n$
; here a permutation of the places
$w_1, \dots, w_n$
; here a permutation of the places
![]() $w_1,\dots, w_n$
yields an isomorphism
$w_1,\dots, w_n$
yields an isomorphism
The argument used in the proof of Lemma 2·6 implies
![]() $\textbf{SU}(h_j)\left(\mathbb{A}^f_k\right) \cong \textbf{SU}(h_i)\!\left(\mathbb{A}_k^f\right)$
and we can proceed as above to obtain the lattices
$\textbf{SU}(h_j)\left(\mathbb{A}^f_k\right) \cong \textbf{SU}(h_i)\!\left(\mathbb{A}_k^f\right)$
and we can proceed as above to obtain the lattices
![]() $\Gamma_1, \dots, \Gamma_n$
as arithmetic subgroups of
$\Gamma_1, \dots, \Gamma_n$
as arithmetic subgroups of
![]() $\Gamma_j \subseteq \textbf{SU}(h_j)(k)$
.
$\Gamma_j \subseteq \textbf{SU}(h_j)(k)$
.
3·4. Type
 $D_\bullet:$
$D_\bullet:$
 $\text{SO}^0(r,s)$
with
$\text{SO}^0(r,s)$
with
 $r+s$
even and
$r+s$
even and
 $r+s \ge 8$
and
$r+s \ge 8$
and
 $\text{SO}_8(\mathbb{C})$
$\text{SO}_8(\mathbb{C})$
Fix an odd prime number p which completely splits in k and let
![]() $w_1,\dots,w_n$
denote the finite places of k dividing p. We fix an additional finite place
$w_1,\dots,w_n$
denote the finite places of k dividing p. We fix an additional finite place
![]() $w^0 \in V_f(k)$
which is distinct from
$w^0 \in V_f(k)$
which is distinct from
![]() $w_1,\dots,w_n$
.
$w_1,\dots,w_n$
.
3·4·1.
 $\text{SO}^0(r,s)$
with
$\text{SO}^0(r,s)$
with
 $r+s$
even and
$r+s$
even and
 $r+s \ge 8$
$r+s \ge 8$
The argument here is similar to the argument above for
![]() $\textrm{SU}(r,s)$
, now using the corresponding local-global principle for quadratic forms. Recall that quadratic forms over
$\textrm{SU}(r,s)$
, now using the corresponding local-global principle for quadratic forms. Recall that quadratic forms over
![]() $\mathbb{R}$
are classified by their dimension and signature; quadratic forms over p-adic fields are classified by dimension, determinant (modulo squares) and the Hasse invariant (see [
Reference Scharlau28
, section 6·4]).
$\mathbb{R}$
are classified by their dimension and signature; quadratic forms over p-adic fields are classified by dimension, determinant (modulo squares) and the Hasse invariant (see [
Reference Scharlau28
, section 6·4]).
Let k be of type I. We will use [
Reference Scharlau28
, chapter 6, theorem 6·10] to construct quadratic forms
![]() $q_1,\dots,q_n$
of dimension
$q_1,\dots,q_n$
of dimension
![]() $r+s$
over k such that:
$r+s$
over k such that:
-
(i)
 $q_j$
has signature (r, s) at the first real place but is positive definite over all other real places;
$q_j$
has signature (r, s) at the first real place but is positive definite over all other real places; -
(ii)
 $q_1, \dots, q_n$
are isometric at every finite place outside
$q_1, \dots, q_n$
are isometric at every finite place outside
 $w_1, \dots, w_n$
;
$w_1, \dots, w_n$
; -
(iii)
 $q_i$
is non-split at the place
$q_i$
is non-split at the place
 $w_i$
, but split at
$w_i$
, but split at
 $w_j$
for all
$w_j$
for all
 $j \neq i$
.
$j \neq i$
.
In addition, we can achieve that
![]() $\textbf{Spin}(q_i)(k_{w_i}) \cong \textbf{Spin}(q_j)(k_{w_j})$
as topological groups for all i, j, which entails
$\textbf{Spin}(q_i)(k_{w_i}) \cong \textbf{Spin}(q_j)(k_{w_j})$
as topological groups for all i, j, which entails
using the argument of Lemma 2·6. By a result of Kneser, the groups
![]() $\textbf{Spin}(q_j)$
have CSP; see [
Reference Kneser14
, 11·1]. As before, it follows from Theorems 2·5 and 2·7 that arithmetic subgroups of the algebraic groups
$\textbf{Spin}(q_j)$
have CSP; see [
Reference Kneser14
, 11·1]. As before, it follows from Theorems 2·5 and 2·7 that arithmetic subgroups of the algebraic groups
![]() $\textbf{Spin}(q_j)$
give rise to profinitely commensurable cocompact lattices in
$\textbf{Spin}(q_j)$
give rise to profinitely commensurable cocompact lattices in
![]() $\textrm{SO}^0(r,s)$
which are not commensurable.
$\textrm{SO}^0(r,s)$
which are not commensurable.
By weak approximation, there is an element
![]() $a \in k^\times$
such that
$a \in k^\times$
such that
![]() $({-}1)^s a$
is positive at the first real place, a is positive at all other real places and such that
$({-}1)^s a$
is positive at the first real place, a is positive at all other real places and such that
![]() $({-}1)^{(r+s)/2}a$
is a square in
$({-}1)^{(r+s)/2}a$
is a square in
![]() $k_{w_i}$
for all
$k_{w_i}$
for all
![]() $i \in \{1,2,\dots,n\}$
. We define
$i \in \{1,2,\dots,n\}$
. We define
![]() $q_j$
to be the unique form of determinant a which has signature (r, s) at the first real place, is positive definite at all other real places, has Hasse invariant
$q_j$
to be the unique form of determinant a which has signature (r, s) at the first real place, is positive definite at all other real places, has Hasse invariant
![]() $-1$
at
$-1$
at
![]() $w_j$
, and has Hasse invariant 1 at the finite places not equal to
$w_j$
, and has Hasse invariant 1 at the finite places not equal to
![]() $w^0, w_j$
. The Hasse invariant at
$w^0, w_j$
. The Hasse invariant at
![]() $w^0$
is then determined by the product formula. It depends on r, s, and n, but not on j.
$w^0$
is then determined by the product formula. It depends on r, s, and n, but not on j.
We observe that
![]() $q_j$
is split at
$q_j$
is split at
![]() $w_i$
for all
$w_i$
for all
![]() $i \neq j$
, since
$i \neq j$
, since
![]() $q_j$
has
$q_j$
has
![]() $r+s$
variables, and the determinant
$r+s$
variables, and the determinant
![]() $({-}1)^{(r+s)/2}$
(i.e., a modulo squares) and the Hasse invariant 1 are equal to the determinant and Hasse invariant of the
$({-}1)^{(r+s)/2}$
(i.e., a modulo squares) and the Hasse invariant 1 are equal to the determinant and Hasse invariant of the
![]() $(r+s)/2$
-fold orthogonal sum of hyperbolic planes
$(r+s)/2$
-fold orthogonal sum of hyperbolic planes
![]() $\langle 1, -1 \rangle$
. On the other hand,
$\langle 1, -1 \rangle$
. On the other hand,
![]() $q_j$
is non-split at
$q_j$
is non-split at
![]() $w_j$
, because the Hasse invariant of
$w_j$
, because the Hasse invariant of
![]() $q_j$
and the split form differ. We observe that modulo the canonical isomorphism
$q_j$
and the split form differ. We observe that modulo the canonical isomorphism
![]() $k_{w_i} \cong \mathbb{Q}_p \cong k_{w_j}$
the forms are isometric and hence the groups
$k_{w_i} \cong \mathbb{Q}_p \cong k_{w_j}$
the forms are isometric and hence the groups
![]() $\textbf{Spin}(q_i)(k_{w_i})$
and
$\textbf{Spin}(q_i)(k_{w_i})$
and
![]() $\textbf{Spin}(q_j)(k_{w_j})$
are isomorphic as topological groups. However, for
$\textbf{Spin}(q_j)(k_{w_j})$
are isomorphic as topological groups. However, for
![]() $i\neq j$
the Witt indices of
$i\neq j$
the Witt indices of
![]() $q_i$
and
$q_i$
and
![]() $q_j$
at
$q_j$
at
![]() $w_j$
differ, hence the
$w_j$
differ, hence the
![]() $k_{w_j}$
-rank of the groups
$k_{w_j}$
-rank of the groups
![]() $\textbf{Spin}(q_i)$
and
$\textbf{Spin}(q_i)$
and
![]() $\textbf{Spin}(q_j)$
are different. So these algebraic groups are not isomorphic over k. Note that our discussion also covers the group
$\textbf{Spin}(q_j)$
are different. So these algebraic groups are not isomorphic over k. Note that our discussion also covers the group
![]() $G = \textrm{SO}^*(8)$
which happens to be locally isomorphic to
$G = \textrm{SO}^*(8)$
which happens to be locally isomorphic to
![]() $\textrm{SO}^0(6,2)$
.
$\textrm{SO}^0(6,2)$
.
3·4·2.
 $\text{SO}_{8}(\mathbb{C})$
$\text{SO}_{8}(\mathbb{C})$
Let k be of type II. Recall that
![]() $w_1,\dots,w_n$
denote the finite places of k dividing p and
$w_1,\dots,w_n$
denote the finite places of k dividing p and
![]() $w^0$
denotes a finite place away from p. For
$w^0$
denotes a finite place away from p. For
![]() $i = 1, \ldots, n$
, there exists a non-degenerate quadratic k-form
$i = 1, \ldots, n$
, there exists a non-degenerate quadratic k-form
![]() $q_i$
of rank eight, with trivial determinant, such that
$q_i$
of rank eight, with trivial determinant, such that
![]() $q_i$
is anisotropic at all real places of k, such that it has Hasse invariant
$q_i$
is anisotropic at all real places of k, such that it has Hasse invariant
![]() $-1$
at
$-1$
at
![]() $w_i$
and
$w_i$
and
![]() $w^0$
, and such that it has Hasse invariant 1 elsewhere. Over
$w^0$
, and such that it has Hasse invariant 1 elsewhere. Over
![]() $\mathbb{Q}_p$
, every nondegenerate quadratic form in at least four variables represents 1. For
$\mathbb{Q}_p$
, every nondegenerate quadratic form in at least four variables represents 1. For
![]() $j = 1, \ldots, n$
, we thus have a decomposition
$j = 1, \ldots, n$
, we thus have a decomposition
![]() $q_i \otimes_k k_{w_j}\cong \langle 1, 1, 1, 1 \rangle \oplus h_{ij}$
for some rank four quadratic
$q_i \otimes_k k_{w_j}\cong \langle 1, 1, 1, 1 \rangle \oplus h_{ij}$
for some rank four quadratic
![]() $\mathbb{Q}_p$
-form
$\mathbb{Q}_p$
-form
![]() $h_{ij}$
with trivial discriminant and the same Hasse invariant as
$h_{ij}$
with trivial discriminant and the same Hasse invariant as
![]() $q_i \otimes_k k_{w_j}$
. By our choice of Hasse invariants,
$q_i \otimes_k k_{w_j}$
. By our choice of Hasse invariants,
![]() $h_{ij}$
is
$h_{ij}$
is
![]() $\mathbb{Q}_p$
-anisotropic if and only if
$\mathbb{Q}_p$
-anisotropic if and only if
![]() $i = j$
[
Reference Serre29
, theorem 6 (iii), p. 36]. Since the form
$i = j$
[
Reference Serre29
, theorem 6 (iii), p. 36]. Since the form
![]() $\langle 1, 1, 1, 1 \rangle$
is metabolic over
$\langle 1, 1, 1, 1 \rangle$
is metabolic over
![]() $\mathbb{Q}_p$
(we assumed p is odd), the form
$\mathbb{Q}_p$
(we assumed p is odd), the form
![]() $q_i$
has Witt index two at
$q_i$
has Witt index two at
![]() $w_i$
and Witt index four at
$w_i$
and Witt index four at
![]() $w_j$
for
$w_j$
for
![]() $j \neq i$
. This shows that the group
$j \neq i$
. This shows that the group
![]() $\textbf{G}_i = \textbf{Spin}(q_i)$
has
$\textbf{G}_i = \textbf{Spin}(q_i)$
has
![]() $\mathbb{Q}_p$
-rank two at
$\mathbb{Q}_p$
-rank two at
![]() $w_i$
and
$w_i$
and
![]() $\mathbb{Q}_p$
-rank four at
$\mathbb{Q}_p$
-rank four at
![]() $w_j$
for
$w_j$
for
![]() $j \neq i$
. The groups
$j \neq i$
. The groups
![]() $\textbf{G}_i$
have moreover CSP by [
Reference Kneser14
, 11·1], so that as above we can conclude that
$\textbf{G}_i$
have moreover CSP by [
Reference Kneser14
, 11·1], so that as above we can conclude that
![]() $\textbf{G}_i(\mathbb{C}) \cong \textbf{Spin}_{\textbf{8}}(\mathbb{C})$
has n profinitely commensurable cocompact lattices which are not commensurable.
$\textbf{G}_i(\mathbb{C}) \cong \textbf{Spin}_{\textbf{8}}(\mathbb{C})$
has n profinitely commensurable cocompact lattices which are not commensurable.
3·5. The remaining real forms
Suppose G is locally isomorphic to
![]() $\textbf{G}(\mathbb{R})$
, where
$\textbf{G}(\mathbb{R})$
, where
![]() $\textbf{G}$
is a connected, simply connected absolutely almost simple algebraic
$\textbf{G}$
is a connected, simply connected absolutely almost simple algebraic
![]() $\mathbb{R}$
-group. Assume that
$\mathbb{R}$
-group. Assume that
![]() $\textbf{G}$
is neither of type
$\textbf{G}$
is neither of type
![]() $A_m$
,
$A_m$
,
![]() $E_6$
, nor isomorphic to
$E_6$
, nor isomorphic to
![]() $\textbf{Spin}(r,s)$
. Let
$\textbf{Spin}(r,s)$
. Let
![]() $\textbf{G}^{u}$
be the compact real form of
$\textbf{G}^{u}$
be the compact real form of
![]() $\textbf{G}$
. Under these assumptions
$\textbf{G}$
. Under these assumptions
![]() $\textbf{G}^{u}$
is an inner form of
$\textbf{G}^{u}$
is an inner form of
![]() $\textbf{G}$
as we saw in Section 3·2. Let
$\textbf{G}$
as we saw in Section 3·2. Let
![]() $\textbf{G}_{\text{qs}}$
denote the unique quasi-split inner form of
$\textbf{G}_{\text{qs}}$
denote the unique quasi-split inner form of
![]() $\textbf{G}$
and
$\textbf{G}$
and
![]() $\textbf{G}^{u}$
.
$\textbf{G}^{u}$
.
Let k be of type I. By [
Reference Borel and Harder4
, proposition 1·10], we can choose a quasi-split, absolutely simple, simply connected algebraic group
![]() $\textbf{G}^0_{\text{qs}}$
over k such that
$\textbf{G}^0_{\text{qs}}$
over k such that
![]() $\textbf{G}^0_{\text{qs}} \times_k k_i \cong \textbf{G}_{\text{qs}}$
for every
$\textbf{G}^0_{\text{qs}} \times_k k_i \cong \textbf{G}_{\text{qs}}$
for every
![]() $i \in \{1,2,\dots,n\}$
. Fix a nonarchimedean place
$i \in \{1,2,\dots,n\}$
. Fix a nonarchimedean place
![]() $w^0 \in V_f(k)$
. Then by [
Reference Prasad and Rapinchuk24
, theorem 1], for
$w^0 \in V_f(k)$
. Then by [
Reference Prasad and Rapinchuk24
, theorem 1], for
![]() $i = 1, \ldots, n$
, there exists an inner k-twist
$i = 1, \ldots, n$
, there exists an inner k-twist
![]() $\textbf{G}_{\textbf{i}}$
of
$\textbf{G}_{\textbf{i}}$
of
![]() $\textbf{G}^0_{\text{qs}}$
such that
$\textbf{G}^0_{\text{qs}}$
such that
-
(i)
 $\textbf{G}_{\textbf{i}} \times_k k_i$
is isomorphic to
$\textbf{G}_{\textbf{i}} \times_k k_i$
is isomorphic to
 $\textbf{G}$
while
$\textbf{G}$
while -
(ii)
 $\textbf{G}_{\textbf{i}} \times_k k_j$
is isomorphic to
$\textbf{G}_{\textbf{i}} \times_k k_j$
is isomorphic to
 $\textbf{G}^{u}$
for
$\textbf{G}^{u}$
for
 $j \neq i$
and
$j \neq i$
and -
(iii)
 $\textbf{G}_{\textbf{i}}$
is isomorphic to
$\textbf{G}_{\textbf{i}}$
is isomorphic to
 $\textbf{G}^0_{\text{qs}}$
at every finite place
$\textbf{G}^0_{\text{qs}}$
at every finite place
 $w \neq w^0$
.
$w \neq w^0$
.
Here, it is essential that
![]() $\textbf{G}$
and
$\textbf{G}$
and
![]() $\textbf{G}^{u}$
are inner twists of each other. Over
$\textbf{G}^{u}$
are inner twists of each other. Over
![]() $\mathfrak{p}$
-adic fields, there only exist a finite number of inner twists of a given absolutely simple group. More precisely, in our context the non-abelian Galois cohomology
$\mathfrak{p}$
-adic fields, there only exist a finite number of inner twists of a given absolutely simple group. More precisely, in our context the non-abelian Galois cohomology
![]() $H^1(k_{w^0}, \textrm{Ad}(\textbf{G}_{\textbf{i}})) \cong $
$H^1(k_{w^0}, \textrm{Ad}(\textbf{G}_{\textbf{i}})) \cong $
![]() $H^2(k_{w^0}, Z(\textbf{G}_{\textbf{i}}))$
has cardinality at most four [
Reference Kneser13
, Satz 2 and table on p. 254] because we assume
$H^2(k_{w^0}, Z(\textbf{G}_{\textbf{i}}))$
has cardinality at most four [
Reference Kneser13
, Satz 2 and table on p. 254] because we assume
![]() $\textbf{G}$
, hence
$\textbf{G}$
, hence
![]() $\textbf{G}_{\textbf{i}}$
, is not of type
$\textbf{G}_{\textbf{i}}$
, is not of type
![]() $A_m$
. Hence if
$A_m$
. Hence if
![]() $n > 4(n^{\prime}-1)$
, the pigeon hole principle guarantees that at least n
′ of the groups
$n > 4(n^{\prime}-1)$
, the pigeon hole principle guarantees that at least n
′ of the groups
![]() $\textbf{G}_{\textbf{1}}, \ldots, \textbf{G}_{\textbf{n}}$
are isomorphic at all finite places. Without loss of generality, let us assume that the first n
′ groups
$\textbf{G}_{\textbf{1}}, \ldots, \textbf{G}_{\textbf{n}}$
are isomorphic at all finite places. Without loss of generality, let us assume that the first n
′ groups
![]() $\textbf{G}_{\textbf{1}}, \ldots, \textbf{G}_{\textbf{n}^{\prime}}$
have this property; in particular, by Lemma 2·6,
$\textbf{G}_{\textbf{1}}, \ldots, \textbf{G}_{\textbf{n}^{\prime}}$
have this property; in particular, by Lemma 2·6,
Pick arithmetic subgroups
![]() $\Gamma_i \subseteq \textbf{G}_{\textbf{i}}(k)$
. The k-group
$\Gamma_i \subseteq \textbf{G}_{\textbf{i}}(k)$
. The k-group
![]() $\textbf{G}_{\textbf{i}}$
is neither of type
$\textbf{G}_{\textbf{i}}$
is neither of type
![]() $A_m$
, nor
$A_m$
, nor
![]() $E_6$
, nor
$E_6$
, nor
![]() $D_4$
(in which case it would be a spinor group) and we have
$D_4$
(in which case it would be a spinor group) and we have
![]() $\textrm{rank}_{k_{i}} \textbf{G}_{\textbf{i}}= \textrm{rank} G \ge 2$
. Hence the congruence kernel
$\textrm{rank}_{k_{i}} \textbf{G}_{\textbf{i}}= \textrm{rank} G \ge 2$
. Hence the congruence kernel
![]() $C(k, \textbf{G}_i)$
has order at most two by Theorem 2·4.
$C(k, \textbf{G}_i)$
has order at most two by Theorem 2·4.
One more time, by Theorem 2·5 and Theorem 2·7, we obtain n
′ profinitely commensurable but non-commensurable cocompact lattices
![]() $\Gamma_1, \dots, \Gamma_{n^{\prime}}$
in
$\Gamma_1, \dots, \Gamma_{n^{\prime}}$
in
![]() $\textbf{G}(\mathbb{R})$
.
$\textbf{G}(\mathbb{R})$
.
3·6. The remaining complex forms
Finally, let
![]() $\textbf{G}$
be a simply connected simple
$\textbf{G}$
be a simply connected simple
![]() $\mathbb{C}$
-group of type
$\mathbb{C}$
-group of type
![]() $B_m$
(
$B_m$
(
![]() $m \ge 2$
),
$m \ge 2$
),
![]() $C_m$
(
$C_m$
(
![]() $m \ge 2$
),
$m \ge 2$
),
![]() $D_m$
(
$D_m$
(
![]() $m \ge 5$
) or
$m \ge 5$
) or
![]() $E_7$
. In the following, all uniqueness statements for algebraic groups are meant up to isomorphism over the field of definition of the group. Let
$E_7$
. In the following, all uniqueness statements for algebraic groups are meant up to isomorphism over the field of definition of the group. Let
![]() $\textbf{G}^u$
be the unique
$\textbf{G}^u$
be the unique
![]() $\mathbb{R}$
-anisotropic
$\mathbb{R}$
-anisotropic
![]() $\mathbb{R}$
-group with
$\mathbb{R}$
-group with
![]() $\textbf{G}^u \times_\mathbb{R} \mathbb{C} = \textbf{G}$
. Let the
$\textbf{G}^u \times_\mathbb{R} \mathbb{C} = \textbf{G}$
. Let the
![]() $\mathbb{R}$
-group
$\mathbb{R}$
-group
![]() $\textbf{G}_{\text{qs}}$
be the unique quasi split inner twist of
$\textbf{G}_{\text{qs}}$
be the unique quasi split inner twist of
![]() $\textbf{G}^u$
. Finally, let
$\textbf{G}^u$
. Finally, let
![]() $\textbf{G}^0$
be the unique
$\textbf{G}^0$
be the unique
![]() $\mathbb{Q}$
-split
$\mathbb{Q}$
-split
![]() $\mathbb{Q}$
-group with
$\mathbb{Q}$
-group with
![]() $\textbf{G}^0 \times_\mathbb{Q} \mathbb{C} = \textbf{G}$
.
$\textbf{G}^0 \times_\mathbb{Q} \mathbb{C} = \textbf{G}$
.
Let k be of type II. Fix an odd prime p that splits in k and let
![]() $w_1, \ldots, w_n$
be the places of k over p. By [
Reference Borel and Harder4
, proposition 1·10], we find a quasi-split, absolutely simple, simply connected algebraic group
$w_1, \ldots, w_n$
be the places of k over p. By [
Reference Borel and Harder4
, proposition 1·10], we find a quasi-split, absolutely simple, simply connected algebraic group
![]() $\textbf{G}^0_{\text{qs}}$
over k which is isomorphic to
$\textbf{G}^0_{\text{qs}}$
over k which is isomorphic to
![]() $\textbf{G}_{\text{qs}}$
at all real places of k and is isomorphic to
$\textbf{G}_{\text{qs}}$
at all real places of k and is isomorphic to
![]() $\textbf{G}^0 \times \mathbb{Q}_p$
at
$\textbf{G}^0 \times \mathbb{Q}_p$
at
![]() $w_1, \ldots, w_n$
. According to Kneser [
Reference Kneser13
, Satz 2 and table on p. 254], our assumption on the type of
$w_1, \ldots, w_n$
. According to Kneser [
Reference Kneser13
, Satz 2 and table on p. 254], our assumption on the type of
![]() $\textbf{G}$
implies that there exists a non-trivial inner
$\textbf{G}$
implies that there exists a non-trivial inner
![]() $\mathbb{Q}_p$
-twist
$\mathbb{Q}_p$
-twist
![]() $\textbf{G}^p$
of
$\textbf{G}^p$
of
![]() $\textbf{G}^0 \times_\mathbb{Q} \mathbb{Q}_p$
. Fix another non-archimedian place
$\textbf{G}^0 \times_\mathbb{Q} \mathbb{Q}_p$
. Fix another non-archimedian place
![]() $w^0$
which does not lie over p. By [
Reference Prasad and Rapinchuk24
, theorem 1], for each
$w^0$
which does not lie over p. By [
Reference Prasad and Rapinchuk24
, theorem 1], for each
![]() $i = 1, \ldots, n$
, there exists an inner k-twist
$i = 1, \ldots, n$
, there exists an inner k-twist
![]() $\textbf{G}_{\textbf{i}}$
of
$\textbf{G}_{\textbf{i}}$
of
![]() $\textbf{G}^0_{\text{qs}}$
such that:
$\textbf{G}^0_{\text{qs}}$
such that:
-
(i)
 $\textbf{G}_{\textbf{i}}$
is isomorphic to
$\textbf{G}_{\textbf{i}}$
is isomorphic to
 $\textbf{G}^u$
at every real place of k;
$\textbf{G}^u$
at every real place of k; -
(ii)
 $\textbf{G}_{\textbf{i}} \times_k k_{w_i}$
is isomorphic to
$\textbf{G}_{\textbf{i}} \times_k k_{w_i}$
is isomorphic to
 $\textbf{G}^p$
,
$\textbf{G}^p$
, -
(iii)
 $\textbf{G}_{\textbf{i}} \times_k k_{w_j}$
is isomorphic to
$\textbf{G}_{\textbf{i}} \times_k k_{w_j}$
is isomorphic to
 $\textbf{G}^0 \times_\mathbb{Q} \mathbb{Q}_p$
for
$\textbf{G}^0 \times_\mathbb{Q} \mathbb{Q}_p$
for
 $j \neq i$
;
$j \neq i$
; -
(iv)
 $\textbf{G}_{\textbf{i}}$
is isomorphic to
$\textbf{G}_{\textbf{i}}$
is isomorphic to
 $\textbf{G}^0_{\text{qs}}$
at every finite place
$\textbf{G}^0_{\text{qs}}$
at every finite place
 $w \notin \left\{w^0, w_1, \ldots, w_n\right\}$
.
$w \notin \left\{w^0, w_1, \ldots, w_n\right\}$
.
By the same pigeon hole argument as above, we may assume that the first n
′ groups
![]() $\textbf{G}_{\textbf{1}}, \ldots, \textbf{G}_{\textbf{n}^{\prime}}$
are also isomorphic at
$\textbf{G}_{\textbf{1}}, \ldots, \textbf{G}_{\textbf{n}^{\prime}}$
are also isomorphic at
![]() $w^0$
. Since p splits in k, swapping any two places over p defines an automorphism of
$w^0$
. Since p splits in k, swapping any two places over p defines an automorphism of
![]() $\mathbb{A}_k^f$
. It follows from the argument in Lemma 2·6 that the groups
$\mathbb{A}_k^f$
. It follows from the argument in Lemma 2·6 that the groups
![]() $\textbf{G}_{\textbf{1}}\!\left(\mathbb{A}_k^f\right), \ldots, \textbf{G}_{\textbf{n}^{\prime}}\!\left(\mathbb{A}_k^f\right)$
are pairwise isomorphic as topological groups. Since CSP is known for
$\textbf{G}_{\textbf{1}}\!\left(\mathbb{A}_k^f\right), \ldots, \textbf{G}_{\textbf{n}^{\prime}}\!\left(\mathbb{A}_k^f\right)$
are pairwise isomorphic as topological groups. Since CSP is known for
![]() $\textbf{G}_{\textbf{i}}$
by Theorem 2·4, any arithmetic subgroups
$\textbf{G}_{\textbf{i}}$
by Theorem 2·4, any arithmetic subgroups
![]() $\Gamma_1, \ldots, \Gamma_{n^{\prime}}$
of
$\Gamma_1, \ldots, \Gamma_{n^{\prime}}$
of
![]() $\textbf{G}_1, \ldots, \textbf{G}_{n^{\prime}}$
are pairwise profinitely commensurable cocompact lattices in
$\textbf{G}_1, \ldots, \textbf{G}_{n^{\prime}}$
are pairwise profinitely commensurable cocompact lattices in
![]() $\textbf{G}(\mathbb{C})$
(Theorem 2·5) which are pairwise non-commensurable because k has no automorphism which could interchange the places
$\textbf{G}(\mathbb{C})$
(Theorem 2·5) which are pairwise non-commensurable because k has no automorphism which could interchange the places
![]() $w_1, \ldots, w_n$
(Theorem 2·7).
$w_1, \ldots, w_n$
(Theorem 2·7).
3·7. Non-cocompact lattices in special linear groups
Our methods above exclusively produce cocompact lattices. To complement this, we sketch a mechanism to come up with profinitely isomorphic, non-commensurable, non-cocompact lattices in special linear groups.
Proposition 3·1. Let G be either
![]() $\text{SL}_m(\mathbb{R})$
,
$\text{SL}_m(\mathbb{R})$
,
![]() $\text{SL}_m(\mathbb{C})$
, or
$\text{SL}_m(\mathbb{C})$
, or
![]() $\text{SL}_m(\mathbb{H})$
where
$\text{SL}_m(\mathbb{H})$
where
![]() $m \geq 6$
is a composite number. Then there are non-cocompact lattices
$m \geq 6$
is a composite number. Then there are non-cocompact lattices
![]() $\Gamma_1, \Gamma_2 \subseteq G$
which are profinitely isomorphic but not commensurable.
$\Gamma_1, \Gamma_2 \subseteq G$
which are profinitely isomorphic but not commensurable.
Proof. Assume that
![]() $G = \textrm{SL}_m(\mathbb{R})$
where
$G = \textrm{SL}_m(\mathbb{R})$
where
![]() $m \geq 6$
is composite. We write
$m \geq 6$
is composite. We write
![]() $m = dk$
with
$m = dk$
with
![]() $d \geq 3$
and
$d \geq 3$
and
![]() $k \geq 2$
. Let C, D be two finite dimensional central division
$k \geq 2$
. Let C, D be two finite dimensional central division
![]() $\mathbb{Q}$
-algebras of degree d, i.e.,
$\mathbb{Q}$
-algebras of degree d, i.e.,
![]() $\dim_\mathbb{Q} C = \dim_\mathbb{Q} D = d^2$
. We assume that for every prime number p, at least one of the algebras
$\dim_\mathbb{Q} C = \dim_\mathbb{Q} D = d^2$
. We assume that for every prime number p, at least one of the algebras
![]() $C_p = \mathbb{Q}_p \otimes_\mathbb{Q} C$
and
$C_p = \mathbb{Q}_p \otimes_\mathbb{Q} C$
and
![]() $D_p = \mathbb{Q}_p \otimes_\mathbb{Q} D$
splits, this means, is isomorphic to
$D_p = \mathbb{Q}_p \otimes_\mathbb{Q} D$
splits, this means, is isomorphic to
![]() $M_d(\mathbb{Q}_p)$
. In addition, we assume that
$M_d(\mathbb{Q}_p)$
. In addition, we assume that
![]() $\mathbb{R} \otimes_\mathbb{Q} C$
and
$\mathbb{R} \otimes_\mathbb{Q} C$
and
![]() $\mathbb{R}\otimes_\mathbb{Q} D$
are split. It follows from the theorem of Albert–Brauer–Hasse–Noether and the resulting description of the Brauer group
$\mathbb{R}\otimes_\mathbb{Q} D$
are split. It follows from the theorem of Albert–Brauer–Hasse–Noether and the resulting description of the Brauer group
![]() $\textrm{Br}(\mathbb{Q})$
(see e.g. [
Reference Pierce20
, section 18·5]), that there are infinitely many such pairs of division algebras (it would be interesting to have concrete examples though).
$\textrm{Br}(\mathbb{Q})$
(see e.g. [
Reference Pierce20
, section 18·5]), that there are infinitely many such pairs of division algebras (it would be interesting to have concrete examples though).
By construction, the central simple algebras
![]() $C \otimes_\mathbb{Q} D$
and
$C \otimes_\mathbb{Q} D$
and
![]() $C\otimes_\mathbb{Q} D^{\text{op}}$
have index d (see [
Reference Pierce20
, section 18·6, corollary]), i.e.,
$C\otimes_\mathbb{Q} D^{\text{op}}$
have index d (see [
Reference Pierce20
, section 18·6, corollary]), i.e.,
for two division
![]() $\mathbb{Q}$
-algebras
$\mathbb{Q}$
-algebras
![]() $E_1, E_2$
of degree d. We define two central simple
$E_1, E_2$
of degree d. We define two central simple
![]() $\mathbb{Q}$
-algebras
$\mathbb{Q}$
-algebras
Since
![]() $d \geq 3$
is the order of [C] and [D] in
$d \geq 3$
is the order of [C] and [D] in
![]() $\textrm{Br}(\mathbb{Q})$
(see [
Reference Pierce20
, section 18·6]), we deduce that the algebras C and D are not isomorphic to their opposite algebras, that is
$\textrm{Br}(\mathbb{Q})$
(see [
Reference Pierce20
, section 18·6]), we deduce that the algebras C and D are not isomorphic to their opposite algebras, that is
![]() $C \not\cong C^{\text{op}}$
and
$C \not\cong C^{\text{op}}$
and
![]() $D \not\cong D^{\text{op}}$
. It follows (using
$D \not\cong D^{\text{op}}$
. It follows (using
![]() $[A] = [E_1] =[C][D]$
and
$[A] = [E_1] =[C][D]$
and
![]() $[B]= [E_2] = [C][D]^{-1}$
in
$[B]= [E_2] = [C][D]^{-1}$
in
![]() $\textrm{Br}(\mathbb{Q})$
) that A is neither isomorphic to B nor to
$\textrm{Br}(\mathbb{Q})$
) that A is neither isomorphic to B nor to
![]() $B^{\text{op}}$
. Therefore, the associated reduced norm-one groups
$B^{\text{op}}$
. Therefore, the associated reduced norm-one groups
![]() $\textbf{G} = \textrm{SL}_1(A)$
and
$\textbf{G} = \textrm{SL}_1(A)$
and
![]() $\textbf{H}=\textrm{SL}_1(B)$
are not isomorphic. In fact, reduced norm-one groups are isomorphic if and only if the underlying algebras are isomorphic or opposite isomorphic (see [
Reference Knus, Merkurjev, Rost and Tignol15
, (26·9) and (26·11)]). For every prime number p we have
$\textbf{H}=\textrm{SL}_1(B)$
are not isomorphic. In fact, reduced norm-one groups are isomorphic if and only if the underlying algebras are isomorphic or opposite isomorphic (see [
Reference Knus, Merkurjev, Rost and Tignol15
, (26·9) and (26·11)]). For every prime number p we have
![]() $\textbf{G}(\mathbb{Q}_p) \cong \textbf{H}(\mathbb{Q}_p)$
. Indeed, suppose C splits at p, then
$\textbf{G}(\mathbb{Q}_p) \cong \textbf{H}(\mathbb{Q}_p)$
. Indeed, suppose C splits at p, then
![]() $E_{1,p} \cong D_p$
and
$E_{1,p} \cong D_p$
and
![]() $E_{2,p}\cong D_p^{\text{op}}$
, and consequently
$E_{2,p}\cong D_p^{\text{op}}$
, and consequently
![]() $A_p = M_{k}(D_p) \cong B_p^{\text{op}}$
. If on the other hand D splits at p, then
$A_p = M_{k}(D_p) \cong B_p^{\text{op}}$
. If on the other hand D splits at p, then
![]() $A_p \cong M_{k}(C_p) \cong B_p$
.
$A_p \cong M_{k}(C_p) \cong B_p$
.
Since C and D split over the real numbers, we have
![]() $\textbf{G}(\mathbb{R}) \cong \textbf{H}(\mathbb{R}) \cong \textrm{SL}_{m}(\mathbb{R})$
. The groups
$\textbf{G}(\mathbb{R}) \cong \textbf{H}(\mathbb{R}) \cong \textrm{SL}_{m}(\mathbb{R})$
. The groups
![]() $\textbf{G}, \textbf{H}$
are isotropic (because
$\textbf{G}, \textbf{H}$
are isotropic (because
![]() $k \geq 2$
) and thus have the congruence subgroup property; see Theorem 2·4. As above, one can show that arithmetic subgroups of
$k \geq 2$
) and thus have the congruence subgroup property; see Theorem 2·4. As above, one can show that arithmetic subgroups of
![]() $\textbf{G}$
and
$\textbf{G}$
and
![]() $\textbf{H}$
are lattices in
$\textbf{H}$
are lattices in
![]() $\textrm{SL}_{m}(\mathbb{R})$
which are profinitely commensurable but not commensurable.
$\textrm{SL}_{m}(\mathbb{R})$
which are profinitely commensurable but not commensurable.
If we replace
![]() $\mathbb{Q}$
by an imaginary quadratic number field, the same construction yields profinitely isomorphic lattices in
$\mathbb{Q}$
by an imaginary quadratic number field, the same construction yields profinitely isomorphic lattices in
![]() $\textrm{SL}_{m}(\mathbb{C})$
. In order to obtain lattices in
$\textrm{SL}_{m}(\mathbb{C})$
. In order to obtain lattices in
![]() $\textrm{SL}_m(\mathbb{H})$
, we vary the argument and write
$\textrm{SL}_m(\mathbb{H})$
, we vary the argument and write
![]() $2m = dk$
as a product of
$2m = dk$
as a product of
![]() $k \geq 2$
and an even number
$k \geq 2$
and an even number
![]() $d \geq 4$
. We choose C, D of degree d as before, now assuming that C is ramified over
$d \geq 4$
. We choose C, D of degree d as before, now assuming that C is ramified over
![]() $\mathbb{R}$
and D splits over
$\mathbb{R}$
and D splits over
![]() $\mathbb{R}$
.
$\mathbb{R}$
.
4. Proof of Theorem 1·2
In this section we show that profinitely commensurable lattices in a connected simple complex Lie group G of type
![]() $E_8$
,
$E_8$
,
![]() $F_4$
, or
$F_4$
, or
![]() $G_2$
are abstractly commensurable. Three features of G are used to conclude Theorem 1·2: G is simply connected, has trivial center, and has no Dynkin diagram symmetries. In particular, G is uniquely determined by its Lie algebra
$G_2$
are abstractly commensurable. Three features of G are used to conclude Theorem 1·2: G is simply connected, has trivial center, and has no Dynkin diagram symmetries. In particular, G is uniquely determined by its Lie algebra
![]() $\mathfrak{g}$
: we have
$\mathfrak{g}$
: we have
![]() $G \cong \textbf{G}(\mathbb{C})$
for the linear algebraic
$G \cong \textbf{G}(\mathbb{C})$
for the linear algebraic
![]() $\mathbb{C}$
-group
$\mathbb{C}$
-group
![]() $\textbf{G} = \textrm{Aut}_\mathbb{C}(\mathfrak{g})$
.
$\textbf{G} = \textrm{Aut}_\mathbb{C}(\mathfrak{g})$
.
So let
![]() $\Gamma_1$
and
$\Gamma_1$
and
![]() $\Gamma_2$
be two profinitely commensurable lattices in
$\Gamma_2$
be two profinitely commensurable lattices in
![]() $\textbf{G}(\mathbb{C})$
. We need to show that
$\textbf{G}(\mathbb{C})$
. We need to show that
![]() $\Gamma_1$
is commensurable with
$\Gamma_1$
is commensurable with
![]() $\Gamma_2$
. By Margulis arithmeticity [
Reference Margulis18
, theorem IX·1·11 and p. 293/294], for
$\Gamma_2$
. By Margulis arithmeticity [
Reference Margulis18
, theorem IX·1·11 and p. 293/294], for
![]() $i=1,2$
, there exists a dense number subfield
$i=1,2$
, there exists a dense number subfield
![]() $k_i \subset \mathbb{C}$
whose remaining infinite places are real and there exists a simply connected absolutely almost simple
$k_i \subset \mathbb{C}$
whose remaining infinite places are real and there exists a simply connected absolutely almost simple
![]() $k_i$
-group
$k_i$
-group
![]() $\textbf{G}_{\textbf{i}}$
which is anisotropic at all real places of
$\textbf{G}_{\textbf{i}}$
which is anisotropic at all real places of
![]() $k_i$
such that for any
$k_i$
such that for any
![]() $k_i$
-embedding
$k_i$
-embedding
![]() $\textbf{G}_{\textbf{i}} \subset \textbf{GL}_{\textbf{r}}$
the group of
$\textbf{G}_{\textbf{i}} \subset \textbf{GL}_{\textbf{r}}$
the group of
![]() $k_i$
-integral points
$k_i$
-integral points
![]() $\textbf{G}_{\textbf{i}}(\mathcal{O}_{k_i})$
is commensurable with
$\textbf{G}_{\textbf{i}}(\mathcal{O}_{k_i})$
is commensurable with
![]() $\Gamma_i$
. Since commensurable groups are also profintely commensurable, it follows that
$\Gamma_i$
. Since commensurable groups are also profintely commensurable, it follows that
![]() $\textbf{G}_{\textbf{1}}(\mathcal{O}_{k_1})$
is profinitely commensurable with
$\textbf{G}_{\textbf{1}}(\mathcal{O}_{k_1})$
is profinitely commensurable with
![]() $\textbf{G}_{\textbf{2}}(\mathcal{O}_{k_2})$
. Consequently by [
Reference Kammeyer11
, theorem 4],
$\textbf{G}_{\textbf{2}}(\mathcal{O}_{k_2})$
. Consequently by [
Reference Kammeyer11
, theorem 4],
![]() $k_1$
is arithmetically equivalent to
$k_1$
is arithmetically equivalent to
![]() $k_2$
. From [
Reference Chinburg, Hamilton, Long and Reid6
, corollary 1·4], we conclude that actually
$k_2$
. From [
Reference Chinburg, Hamilton, Long and Reid6
, corollary 1·4], we conclude that actually
![]() $k_1$
is abstractly isomorphic to
$k_1$
is abstractly isomorphic to
![]() $k_2$
, hence the two subfields of
$k_2$
, hence the two subfields of
![]() $\mathbb{C}$
are either equal or complex conjugates of one another. Replacing
$\mathbb{C}$
are either equal or complex conjugates of one another. Replacing
![]() $k_2$
and
$k_2$
and
![]() $\textbf{G}_{\textbf{2}}$
with the complex conjugate field and group if need be, we may assume
$\textbf{G}_{\textbf{2}}$
with the complex conjugate field and group if need be, we may assume
![]() $k_1 = k_2 = k$
.
$k_1 = k_2 = k$
.
Again owing to the exceptional type at hand, the groups
![]() $\textbf{G}_{\textbf{i}}$
have trivial center and no Dynkin diagram symmetries. We thus have
$\textbf{G}_{\textbf{i}}$
have trivial center and no Dynkin diagram symmetries. We thus have
![]() $\textrm{Aut}(\textbf{G}_{\textbf{i}}) \cong \textbf{G}_{\textbf{i}}$
, so the k-isomorphism type of
$\textrm{Aut}(\textbf{G}_{\textbf{i}}) \cong \textbf{G}_{\textbf{i}}$
, so the k-isomorphism type of
![]() $\textbf{G}_{\textbf{2}}$
is classified by a class
$\textbf{G}_{\textbf{2}}$
is classified by a class
![]() $\alpha \in H^1(k, \textbf{G}_{\textbf{1}})$
in non-commutative Galois cohomology with values in
$\alpha \in H^1(k, \textbf{G}_{\textbf{1}})$
in non-commutative Galois cohomology with values in
![]() $\textbf{G}_{\textbf{1}}$
. Since
$\textbf{G}_{\textbf{1}}$
. Since
![]() $\textbf{G}_{\textbf{1}}$
is isomorphic to
$\textbf{G}_{\textbf{1}}$
is isomorphic to
![]() $\textbf{G}_{\textbf{2}}$
at all infinite places of k, we see that
$\textbf{G}_{\textbf{2}}$
at all infinite places of k, we see that
![]() $\alpha$
reduces to the distinguished point in
$\alpha$
reduces to the distinguished point in
![]() $H^1(k_v, \textbf{G}_{\textbf{1}})$
for all
$H^1(k_v, \textbf{G}_{\textbf{1}})$
for all
![]() $v \in V_\infty(k)$
. But by the main theorem of Galois cohomology of simply connected groups [
Reference Platonov and Rapinchuk21
, Theorem 6.6, p. 289], we have a bijection of pointed sets
$v \in V_\infty(k)$
. But by the main theorem of Galois cohomology of simply connected groups [
Reference Platonov and Rapinchuk21
, Theorem 6.6, p. 289], we have a bijection of pointed sets
So
![]() $\alpha$
is the trivial twist, hence
$\alpha$
is the trivial twist, hence
![]() $\textbf{G}_{\textbf{1}}$
is k-isomorphic to
$\textbf{G}_{\textbf{1}}$
is k-isomorphic to
![]() $\textbf{G}_{\textbf{2}}$
. In particular,
$\textbf{G}_{\textbf{2}}$
. In particular,
![]() $\textbf{G}_{\textbf{1}}(\mathcal{O}_k)$
is commensurable with
$\textbf{G}_{\textbf{1}}(\mathcal{O}_k)$
is commensurable with
![]() $\textbf{G}_{\textbf{2}}(\mathcal{O}_k)$
, and so is
$\textbf{G}_{\textbf{2}}(\mathcal{O}_k)$
, and so is
![]() $\Gamma_1$
with
$\Gamma_1$
with
![]() $\Gamma_2$
.
$\Gamma_2$
.
5. Proof of Theorem 1·3
Finally, in this section we give the proof of Theorem 1·3. Let
![]() $\mathfrak{g}$
be the Lie algebra of G. The simple linear algebraic
$\mathfrak{g}$
be the Lie algebra of G. The simple linear algebraic
![]() $\mathbb{R}$
-group
$\mathbb{R}$
-group
![]() $\textbf{G}_{\text{ad}} = \textrm{Aut}_\mathbb{R}(\mathfrak{g})$
, satisfies
$\textbf{G}_{\text{ad}} = \textrm{Aut}_\mathbb{R}(\mathfrak{g})$
, satisfies
![]() $\textbf{G}_{\text{ad}}(\mathbb{R})^0 = G$
. Let
$\textbf{G}_{\text{ad}}(\mathbb{R})^0 = G$
. Let
![]() $\widetilde{\textbf{G}}$
be the simply connected covering of
$\widetilde{\textbf{G}}$
be the simply connected covering of
![]() $\textbf{G}_{\text{ad}}$
. We will construct profinitely isomorphic, non-isomorphic cocompact lattices
$\textbf{G}_{\text{ad}}$
. We will construct profinitely isomorphic, non-isomorphic cocompact lattices
![]() $\Gamma_1,\dots, \Gamma_n \subseteq \widetilde{\textbf{G}}(\mathbb{R})$
which do not intersect the center and are thus isomorphic to lattices in G.
$\Gamma_1,\dots, \Gamma_n \subseteq \widetilde{\textbf{G}}(\mathbb{R})$
which do not intersect the center and are thus isomorphic to lattices in G.
If
![]() $\widetilde{\textbf{G}}$
is absolutely simple, then we take k of type I and set
$\widetilde{\textbf{G}}$
is absolutely simple, then we take k of type I and set
![]() $\textbf{G} = \widetilde{\textbf{G}}$
. If
$\textbf{G} = \widetilde{\textbf{G}}$
. If
![]() $\widetilde{\textbf{G}}$
is not absolutely simple, then
$\widetilde{\textbf{G}}$
is not absolutely simple, then
![]() $\widetilde{\textbf{G}} = \textrm{Res}_{\mathbb{C}/\mathbb{R}}(\textbf{G})$
for a simply connected simple algebraic
$\widetilde{\textbf{G}} = \textrm{Res}_{\mathbb{C}/\mathbb{R}}(\textbf{G})$
for a simply connected simple algebraic
![]() $\mathbb{C}$
-group
$\mathbb{C}$
-group
![]() $\textbf{G}$
. In this case we choose k of type II. Let p be a rational prime number which splits completely in k with finite places
$\textbf{G}$
. In this case we choose k of type II. Let p be a rational prime number which splits completely in k with finite places
![]() $w_1,\dots,w_n$
dividing p and
$w_1,\dots,w_n$
dividing p and
![]() $k_{w_i} \cong \mathbb{Q}_p$
for all i.
$k_{w_i} \cong \mathbb{Q}_p$
for all i.
By Theorem B in [
Reference Borel and Harder4
] there is a simply connected, absolutely simple algebraic k-group
![]() $\textbf{H}$
such that:
$\textbf{H}$
such that:
-
(i)
 $\textbf{H} \times_k k_1 \cong \textbf{G}$
;
$\textbf{H} \times_k k_1 \cong \textbf{G}$
; -
(ii)
 $\textbf{H}(k_j)$
is compact for all
$\textbf{H}(k_j)$
is compact for all
 $j \geq 2$
; and
$j \geq 2$
; and -
(iii)
 $\textbf{H}(k_{w_i}) \cong \textbf{H}(k_{w_j})$
for all
$\textbf{H}(k_{w_i}) \cong \textbf{H}(k_{w_j})$
for all
 $i,j \in \{1,\dots,n\}$
.
$i,j \in \{1,\dots,n\}$
.
If G is of type
![]() $A_m$
(using
$A_m$
(using
![]() $G \neq \textrm{PSL}_m(\mathbb{H})$
) we can take
$G \neq \textrm{PSL}_m(\mathbb{H})$
) we can take
![]() $\textbf{H}$
to be a special unitary group. If G is of type
$\textbf{H}$
to be a special unitary group. If G is of type
![]() $D_4$
, we can take
$D_4$
, we can take
![]() $\textbf{H}$
to be a spinor group. By construction the group
$\textbf{H}$
to be a spinor group. By construction the group
![]() $\textbf{H}$
then has the congruence subgroup property and we can find an arithmetic subgroup
$\textbf{H}$
then has the congruence subgroup property and we can find an arithmetic subgroup
![]() $\Gamma \subseteq \textbf{H}(k)$
which does not intersect the congruence kernel, so that
$\Gamma \subseteq \textbf{H}(k)$
which does not intersect the congruence kernel, so that
![]() $\widehat{\Gamma} \cong \overline{\Gamma} \subseteq \textbf{H}\!\left(\mathbb{A}_k^f\right)$
; here
$\widehat{\Gamma} \cong \overline{\Gamma} \subseteq \textbf{H}\!\left(\mathbb{A}_k^f\right)$
; here
![]() $\overline{\Gamma}$
denotes the closure of
$\overline{\Gamma}$
denotes the closure of
![]() $\Gamma$
in
$\Gamma$
in
![]() $\textbf{H}\!\left(\mathbb{A}_k^f\right)$
. Passing to a finite index subgroup if need be, we may assume that
$\textbf{H}\!\left(\mathbb{A}_k^f\right)$
. Passing to a finite index subgroup if need be, we may assume that
![]() $\Gamma$
intersects the center of
$\Gamma$
intersects the center of
![]() $\textbf{H}$
trivially, too.
$\textbf{H}$
trivially, too.
We decompose the ring of finite adeles as
![]() $\mathbb{A}_k^{f} = \prod_{i=1}^n k_{w_i} \times \mathbb{A}_k^{f,p^{\prime}}$
into the p- and p
′-part. We can find open compact subgroups
$\mathbb{A}_k^{f} = \prod_{i=1}^n k_{w_i} \times \mathbb{A}_k^{f,p^{\prime}}$
into the p- and p
′-part. We can find open compact subgroups
![]() $K_{0,i} \subseteq \textbf{H}(k_{w_i})$
such that
$K_{0,i} \subseteq \textbf{H}(k_{w_i})$
such that
![]() $K_{0,i} \cong K_{0,j}$
for all i, j and such that
$K_{0,i} \cong K_{0,j}$
for all i, j and such that
where
![]() $K_f^{p^{\prime}}$
is some open compact subgroup of
$K_f^{p^{\prime}}$
is some open compact subgroup of
![]() $\textbf{H}\left(\mathbb{A}_k^{f,p^{\prime}}\right)$
. We choose open compact subgroups
$\textbf{H}\left(\mathbb{A}_k^{f,p^{\prime}}\right)$
. We choose open compact subgroups
![]() $K_{1,i} \subseteq K_{0,i}$
again such that
$K_{1,i} \subseteq K_{0,i}$
again such that
![]() $K_{1,i} \cong K_{1,j}$
for all i, j of sufficiently large index satisfying
$K_{1,i} \cong K_{1,j}$
for all i, j of sufficiently large index satisfying
![]() $|K_{0,i}\,:\,K_{1,i}| > |\textbf{Z}(\textbf{H})(k)|$
. Now we define the arithmetic groups
$|K_{0,i}\,:\,K_{1,i}| > |\textbf{Z}(\textbf{H})(k)|$
. Now we define the arithmetic groups
where
![]() $\delta_{i,j}$
is the Kronecker–Delta. By construction
$\delta_{i,j}$
is the Kronecker–Delta. By construction
![]() $\widehat{\Gamma_j} \cong \prod_{i=1}^n K_{\delta_{i,j},i} \times K_f^{p^{\prime}}$
, hence the groups
$\widehat{\Gamma_j} \cong \prod_{i=1}^n K_{\delta_{i,j},i} \times K_f^{p^{\prime}}$
, hence the groups
![]() $\Gamma_1,\dots, \Gamma_n$
are profinitely isomorphic. Being subgroups of
$\Gamma_1,\dots, \Gamma_n$
are profinitely isomorphic. Being subgroups of
![]() $\Gamma$
, they do not intersect the center.
$\Gamma$
, they do not intersect the center.
It remains to prove that the arithmetic groups
![]() $\Gamma_1,\dots,\Gamma_n$
are pairwise non-isomorphic. We explain this for
$\Gamma_1,\dots,\Gamma_n$
are pairwise non-isomorphic. We explain this for
![]() $\Gamma_1$
and
$\Gamma_1$
and
![]() $\Gamma_2$
. Suppose for a contradiction that
$\Gamma_2$
. Suppose for a contradiction that
![]() $\phi \colon \Gamma_1 \to \Gamma_2$
is an isomorphism. As
$\phi \colon \Gamma_1 \to \Gamma_2$
is an isomorphism. As
![]() $\Gamma_2$
is a subgroup of
$\Gamma_2$
is a subgroup of
![]() $\textbf{H}(k)$
, it follows from Margulis superrigidity [
Reference Margulis18
, theorem (5), p.5] (using that k has no automorphisms) that there is an automorphism
$\textbf{H}(k)$
, it follows from Margulis superrigidity [
Reference Margulis18
, theorem (5), p.5] (using that k has no automorphisms) that there is an automorphism
![]() $\eta$
of
$\eta$
of
![]() $\textbf{H}$
defined over k and a homomorphism
$\textbf{H}$
defined over k and a homomorphism
![]() $\nu\colon \Gamma_1 \to \textbf{Z}(\textbf{H})(k)$
such that
$\nu\colon \Gamma_1 \to \textbf{Z}(\textbf{H})(k)$
such that
for all
![]() $\gamma \in \Gamma_1$
. Fix a Haar measure on
$\gamma \in \Gamma_1$
. Fix a Haar measure on
![]() $\textbf{H}(k_{w_1})$
. Using the inclusion of
$\textbf{H}(k_{w_1})$
. Using the inclusion of
![]() $\Gamma_2$
into
$\Gamma_2$
into
![]() $\textbf{H}(k_{w_1})$
, we see that the closure
$\textbf{H}(k_{w_1})$
, we see that the closure
![]() $\overline{\phi(\Gamma_1)}$
of
$\overline{\phi(\Gamma_1)}$
of
![]() $\phi(\Gamma_1)$
in
$\phi(\Gamma_1)$
in
![]() $\textbf{H}(k_{w_1})$
is
$\textbf{H}(k_{w_1})$
is
![]() $K_{0,1}$
. On the other hand,
$K_{0,1}$
. On the other hand,
![]() $\overline{\phi(\Gamma_1)}$
is contained in
$\overline{\phi(\Gamma_1)}$
is contained in
![]() $\textbf{Z}(\textbf{H})(k)\eta(K_{1,1})$
. This can be used to derive a contradiction, since the Haar measure of the latter is strictly smaller than the Haar measure of
$\textbf{Z}(\textbf{H})(k)\eta(K_{1,1})$
. This can be used to derive a contradiction, since the Haar measure of the latter is strictly smaller than the Haar measure of
![]() $K_{0,1}$
. Recall that
$K_{0,1}$
. Recall that
![]() $\textbf{H}(k_1)$
is unimodular [
Reference Margulis18
, I(2·2·3)] and that the inner automorphism group of
$\textbf{H}(k_1)$
is unimodular [
Reference Margulis18
, I(2·2·3)] and that the inner automorphism group of
![]() $\textbf{H}$
has finite index in the automorphism group of
$\textbf{H}$
has finite index in the automorphism group of
![]() $\textbf{H}$
. We deduce that
$\textbf{H}$
. We deduce that
![]() $\eta$
preserves the Haar measure and therefore
$\eta$
preserves the Haar measure and therefore
which is a contradiction.
Acknowledgements
It is our pleasure to thank G. Mantilla Soler and S. Kühnlein for helpful discussions. We are grateful for financial support from the German Research Foundation [DFG 338540207 (SPP 2026/1), DFG 441848266 (SPP 2026/2), and DFG 281869850 (RTG 2229)].