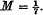Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Davenport, H.
1947.
On the product of three non-homogeneous linear forms.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 43,
Issue. 2,
p.
137.
1950.
Diophantine inequalities with an infinity of solutions.
Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences,
Vol. 242,
Issue. 848,
p.
311.
Chalk, J. H. H.
and
Rogers, C. A.
1951.
On the product of three homogeneous linear forms.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 47,
Issue. 2,
p.
251.
1955.
On the product of three homogeneous linear forms and indefinite ternary quadratic forms.
Philosophical Transactions of the Royal Society of London. Series A, Mathematical and Physical Sciences,
Vol. 248,
Issue. 940,
p.
73.
Cohn, Harvey
1955.
Some Experiments in Ideal Factorization on the MIDAC.
Journal of the ACM,
Vol. 2,
Issue. 2,
p.
111.
Ennola, Veikko
and
Turunen, Reino
1985.
On totally real cubic fields.
Mathematics of Computation,
Vol. 44,
Issue. 170,
p.
495.
1987.
Geometry of Numbers.
Vol. 37,
Issue. ,
p.
632.
Bryuno, A. D.
and
Parusnikov, V. I.
1994.
Klein polyhedrals for two cubic Davenport forms.
Mathematical Notes,
Vol. 56,
Issue. 4,
p.
994.
Bryuno, A. D.
and
Parusnikov, V. I.
1997.
Comparison of various generalizations of continued fractions.
Mathematical Notes,
Vol. 61,
Issue. 3,
p.
278.
Брюно, Александр Дмитриевич
Bruno, Alexander Dmitrievich
Парусников, Владимир Игоревич
and
Parusnikov, Vladimir Igorevich
1997.
Сравнение разных обобщений цепных дробей.
Математические заметки,
Vol. 61,
Issue. 3,
p.
339.
Parusnikov, V. I.
2000.
Klein polyhedra for the fourth extremal cubic form.
Mathematical Notes,
Vol. 67,
Issue. 1,
p.
87.
Парусников, Владимир Игоревич
and
Parusnikov, Vladimir Igorevich
2000.
Многогранники Клейна для четвертой экстремальной кубической формы.
Математические заметки,
Vol. 67,
Issue. 1,
p.
110.
Parusnikov, V. I.
2005.
Klein polyhedra for three extremal cubic forms.
Mathematical Notes,
Vol. 77,
Issue. 3-4,
p.
523.
Парусников, Владимир Игоревич
and
Parusnikov, Vladimir Igorevich
2005.
Многогранники Клейна для трех экстремальных кубических форм.
Математические заметки,
Vol. 77,
Issue. 4,
p.
566.
Karpenkov, Oleg N.
and
Vershik, Anatoly M.
2010.
Rational approximation of maximal commutative subgroups of $${GL(n,\mathbb{R})}$$.
Journal of Fixed Point Theory and Applications,
Vol. 7,
Issue. 1,
p.
241.
Narkiewicz, Władysław
2012.
Rational Number Theory in the 20th Century.
p.
13.
Karpenkov, Oleg
2013.
Geometry of Continued Fractions.
Vol. 26,
Issue. ,
p.
301.
Karpenkov, Oleg
2013.
Geometry of Continued Fractions.
Vol. 26,
Issue. ,
p.
67.
Ustinov, Alexey Vladimirovich
2015.
Трехмерные цепные дроби и суммы Клостермана.
Успехи математических наук,
Vol. 70,
Issue. 3(423),
p.
107.
Karpenkov, Oleg
and
Ustinov, Alexey
2017.
Geometry and combinatoric of Minkowski–Voronoi 3-dimensional continued fractions.
Journal of Number Theory,
Vol. 176,
Issue. ,
p.
375.

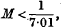
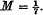 If we denote by θ, ø, ψ the roots of the cubic equation t3+t2-2t-1 = 0, the special linear forms are equivalent, by an integral unimodular linear transformation, to
If we denote by θ, ø, ψ the roots of the cubic equation t3+t2-2t-1 = 0, the special linear forms are equivalent, by an integral unimodular linear transformation, to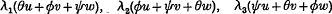
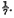 In this case, L1L2L3|λ1λ2λ3 is a non-zero integer, and the minimum of its absolute value is 1, giving
In this case, L1L2L3|λ1λ2λ3 is a non-zero integer, and the minimum of its absolute value is 1, giving