Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-24T13:12:56.145Z Has data issue: false hasContentIssue false
  • English
  • Français

On the non-absolute summability of a Fourier series and the conjugate of a Fourier series by a Nörlund method

Published online by Cambridge University Press:  24 October 2008

R. Mohanty  and
B. K. Ray
R. Mohanty
Affiliation:
Ravenshaw College, Cuttack, India
B. K. Ray
Affiliation:
Ravenshaw College, Cuttack, India
Get access Rights & Permissions [Opens in a new window]

Extract

Let {Sn} be the sequence of partial sums of the infinite seriesΣαn. Let {pn} be a sequence of constants real or complex and let us set

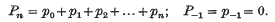
The sequence {tn} of Nörlund means (5) or simply (N, pn) means of the sequence {Sn} generated by the sequence of coefficients {pn} is defined by the following sequence -to-sequence transformation

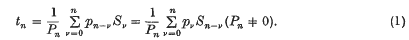
The series ∑αn or the sequence {Sn} is said to be summable (N, pn) to the sum S, if

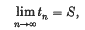
and is said to be absolutely summable (N, pn) or summable |N, pn|, if the sequence {tn} is of bounded variation, that is, the series ∑|tn − tn−1| is convergent (2).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 63 , Issue 2 , April 1967 , pp. 407 - 411
Copyright
Copyright © Cambridge Philosophical Society 1967

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Iyengar, K. S. K.A Tauberian theorem and its application to convergence of Fourier series. Proc. Indian Acad. Sci. 18 (1943), 81–87.Google Scholar
(2)Mears, Florence M.Some multiplication theorems for the Norlund mean. Bull. Amer. Math. Soc. 41 (1935), 875–880.CrossRefGoogle Scholar
(3)Mohanty, R.A criterion for the absolute convergence of a Fourier series. Proc. London Math. Soc. (2) 51 (1949), 186–196.CrossRefGoogle Scholar
(4)Mohanty, R.On the absolute Riesz summability of Fourier series and allied series. Proc. London Math. Soc. (2) 52 (1951), 295–320.Google Scholar
(5)Nörlund, N. E.Sur une application des fonctions permutables. Lunds Univ. Årsskr Avd. 2 16 (1919), no. 3.Google Scholar
(6)Pati, T.The non-absolute summability of Fourier series by a Nörlund Method. J. Indian Math. Soc. 25 (1961), 197–214.Google Scholar
(7)Zygmund, Antoni.Trigonometric series, vol. I, p. 63 (Cambridge University Press, 1959).Google Scholar