Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T04:56:03.494Z Has data issue: false hasContentIssue false
  • English
  • Français

On the motion of a Gaussian wave-packet in a parabolic potential field

Published online by Cambridge University Press:  24 October 2008

C. A. Coulson  and
G. S. Rushbrooke
C. A. Coulson
Affiliation:
Department of Physical ChemistryThe UniversityOxford
G. S. Rushbrooke
Affiliation:
Department of Physical ChemistryThe UniversityLeeds
Get access Rights & Permissions [Opens in a new window]

Extract

The paper deals with the motion of a Gaussian wave-packet in a parabolic potential field, contrasting the quantum-mechanical behaviour of the packet with that which follows from pure classical mechanics.

The behaviour is entirely classical only if the initial phase of the space-wave-function is linear in the space coordinate; in which case the wave-packet is initially a ‘best-possible’ packet according to Heisenberg's uncertainty relationship.

The paper concludes with a brief reference to the similar problem for a free particle.

Note added in Proof, 16 February 1946. Through the courtesy of Mr M. S. Bartlett, we have been privileged to see the manuscripts of some work by Mr J. E. Moyal and himself, in which the motion of a probability wave-packet is discussed in more general terms than our own: and in which it appears that the motion of our wave-packet, which we have described as non-classical, is indeed actually classical provided that a certain correlation exists between momentum and position in the p, q-distribution function. With this knowledge we now find that classical and quantal predictions agree precisely provided that the initial classical probability function is given by

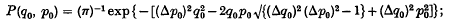
this is a particular case of their more general results.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 42 , Issue 3 , October 1946 , pp. 286 - 291
Copyright
Copyright © Cambridge Philosophical Society 1946

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Rojanski, V.Introductory quantum mechanics (New York, 1938), § 21.Google Scholar
(2)Darwin, C. G.Proc. Roy. Soc. A, 117 (1927), 258.Google Scholar
(3)Kennard, E. H. Z.Phys. 44 (1927), 326.Google Scholar
(4)Whittaker, E. T.Proc. Roy. Soc. Edinb. 61 (1941), 1.Google Scholar
(5)Watson, G. N.J. Lond. Math. Soc. 8 (1933), 194.CrossRefGoogle Scholar
(6)Sommerfeld, A.Wave mechanics (Methuen, 1930), Ch. ii, § 9.Google Scholar