Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-25T21:08:04.006Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Lq norm of cyclotomic Littlewood polynomials on the unit circle

Published online by Cambridge University Press:  13 July 2011

TAMÁS ERDÉLYI
TAMÁS ERDÉLYI*
Affiliation:
Department of Mathematics, Texas A&M University, College Station, Texas 77843, U.S.A. e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 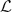n be the collection of all (Littlewood) polynomials of degree n with coefficients in {−1, 1}. In this paper we prove that if (P2ν) is a sequence of cyclotomic polynomials P2ν ∈ 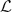2ν, then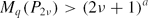for every q > 2 with some a = a(q) > 1/2 depending only on q, where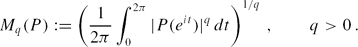The case q = 4 of the above result is due to P. Borwein, Choi and Ferguson. We also prove that if (P2ν) is a sequence of cyclotomic polynomials P2ν ∈ 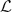2ν, then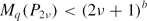for every 0 < q < 2 with some 0 < b = b(q) < 1/2 depending only on q. Similar results are conjectured for Littlewood polynomials of odd degree. Our main tool here is the Borwein–Choi Factorization Theorem.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 151 , Issue 2 , September 2011 , pp. 373 - 384
Copyright
Copyright © Cambridge Philosophical Society 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[Be]Beck, J. “Flat” polynomials on the unit circle – note on a problem of Littlewood. Bull. London Math. Soc. (1991), 269–277.CrossRefGoogle Scholar
[BB]Bombieri, E. and Bourgain, J.On Kahane's ultraflat polynomials. J. Eur. Math. Soc. 11 (2009, 3), 627–703.Google Scholar
[Bo]Borwein, P.Computational excursions in analysis and number theory (Springer-Verlag, 2002).CrossRefGoogle Scholar
[BC]Borwein, P. and Choi, K.S.On cyclotomic polynomials with ± 1 coefficients. Experiment. Math. 8 (1995), 399–407.Google Scholar
[BCF]Borwein, P., Choi, K. S. and Ferguson, R.Norm of Littlewood cyclotomic polynomials. Math. Proc. Camb. Phil. Soc. 138 (2005), 315–326.Google Scholar
[BE]Borwein, P. and Erdélyi, T.Polynomials and polynomial inequalities (Springer-Verlag, 1995).Google Scholar
[BLM]Brillhart, J., Lomont, J.S. and Morton, P.Cyclotomic properties of the Rudin–Shapiro polynomials. J. Reine Angew. Math. 288 (1976), 37–75.Google Scholar
[Em]Eminyan, K. M.The L 1 norm of a trigonometric sum. Math. Notes 76 (2004), 124–132.CrossRefGoogle Scholar
[Er1]Erdélyi, T.The phase problem of ultraflat unimodular polynomials: the resolution of the conjecture of Saffari. Math. Ann. 321 (2001), 905–924.Google Scholar
[Er2]Erdélyi, T.How far is a sequence of ultraflat unimodular polynomials from being conjugate reciprocal. Michigan Math. J. 49 (2001), 259–264.Google Scholar
[Er3]Erdélyi, T.A proof of Saffari's “near-orthogonality" conjecture for ultraflat sequences of unimodular polynomials. C. R. Acad. Sci. Paris Sér. I Math. 333 (2001), 623–628.Google Scholar
[Er4]Erdélyi, T.On the real part of ultraflat sequences of unimodular polynomials: consequences implied by the resolution of the Phase Problem. Math. Ann. 326 (2003), 489–498.Google Scholar
[Er]Erdős, P.Some unsolved problems. Michigan Math. J. 4 (1957), 291–300.CrossRefGoogle Scholar
[GR]Green, B. and Ruzsa, I. Z.On the Hardy–Littlewood majorant problem. Math. Proc. Camb. Phil. Soc. 137 (2004), 511–517.Google Scholar
[Ka]Kahane, J.P.Sur les polynomes a coefficient unimodulaires. Bull. London Math. Soc. 12 (1980), 321–342.Google Scholar
[Ko]Körner, T.On a polynomial of J.S. Byrnes. Bull. London Math. Soc. 12 (1980), 219–224.CrossRefGoogle Scholar
[Li1]Littlewood, J. E.On polynomials ∑ ± z m, ∑exp(αmi)z m, z = e iθ. J. London Math. Soc. 41 (1966), 367–376.Google Scholar
[Li2]Littlewood, J. E. Some problems in real and complex analysis. Heath Mathematical Monographs (Lexington, Massachusetts, 1968).Google Scholar
[QS]Queffelec, H. and Saffari, B.On Bernstein's inequality and Kahane's ultraflat polynomials. J. Fourier Anal. Appl. 2 (1996, 6), 519–582.Google Scholar
[Sa]Saffari, B. The phase behavior of ultraflat unimodular polynomials. In Probabilistic and Stochastic Methods in Analysis, with Applications (Kluwer Academic Publishers, 1992), 555–572.Google Scholar