Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-02T21:12:42.140Z Has data issue: false hasContentIssue false
  • English
  • Français

On the iteration of a continuous mapping of a compact space into itself

Published online by Cambridge University Press:  24 October 2008

F. G. Friedlander
F. G. Friedlander
Affiliation:
The UniversityManchester
Get access Rights & Permissions [Opens in a new window]

Extract

1. The questions considered in this note are suggested by the elementary topology of the trajectories of systems of non-linear differential equations. Such a system may be assumed in the form

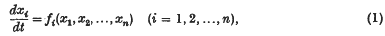
and the values of the dependent variables x1, x2, …, xn at ‘time’ t can be represented by a point P(t) in a ‘phase space’ 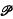. As t varies, P(t) describes a curve in 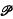, which is a trajectory of (1). Now it often happens that 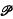contains a subspace E (usually of lower dimension) with the following properties: (i) by considering the trajectories generated by points P(t) which are, for t = 0, in E, all the trajectories of (1) are obtained; (ii) if P(0) is in E, then P(t) is not in E for 0 < t < c, where c is a constant independent of P(0) in E; (iii) if P(0) is in E, then the trajectory meets E again for some finite t at a point P(T) (T is not necessarily the same for all points of E). By considering P(T) as the image of P(O), a mapping of E into itself is defined which is associated with the system (1), and the topology of the trajectories of (1) can be studied conveniently by discussing this mapping. When the functions fi in (1) satisfy the continuity and Lipschitz conditions of the classical existence-and-uniqueness theorem, the mapping is one-one and continuous. The study of this ‘transformation theory’, initiated by Poincaré, has been developed chiefly by G. D. Birkhoff(l,2). His results have been applied to problems of ‘non-linear mechanics’ by N. Levinson(3).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 46 , Issue 1 , January 1950 , pp. 46 - 56
Copyright
Copyright © Cambridge Philosophical Society 1950

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Birkhoff, G. D.Surface transformations and their dynamical applications. Acta Math. 43 (1922), 1–119, especially pp. 100–14.CrossRefGoogle Scholar
(2)Birkhoff, G. D. and Smith, P. A.Structure analysis of surface transformations. J. Math. (ser. ix), 7 (1928), 345–80.Google Scholar
(3)Levinson, N.Transformation theory of non-linear differential equations.… Ann. Math. 45 (1944), 723–37.CrossRefGoogle Scholar
(4)Hall, D. W. and Kelley, J. L.Periodic types of transformations. Duke Math. J. 8 (1941), 625–30.CrossRefGoogle Scholar
(5)Cherry, T. M.Topological properties of the solutions of ordinary differential equations. Amer. J. Math. 59 (1937), 957–82.CrossRefGoogle Scholar
(6)Whyburn, G. T.Analytic topology (New York, 1942), p. 17.Google Scholar
(7)Denjoy, A.Sur les courbes definies par les equations differentielles à la surface du tore. J. Math. (ser. ix), 11 (1032), 333–75.Google Scholar
(8)Gottschalk, W. H.Almost periodic points with respect to transformation semi-groups. Ann. Math. 47 (1946), 762–6.CrossRefGoogle Scholar
(9)Hausdorff, F.Mengenlehre (3rd ed. reprinted New York, undated), p. 145.Google Scholar
(10)Lefschetz, S.Lectures on differential equations (Princeton, 1946).Google Scholar