Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-24T17:22:53.406Z Has data issue: false hasContentIssue false
  • English
  • Français

On the function

Published online by Cambridge University Press:  24 October 2008

A. S. Meligy  and
E. M. EL Gazzy
A. S. Meligy
Affiliation:
Faculty of Science, University of Alexandria, Alexandria, Egypt
E. M. EL Gazzy
Affiliation:
Faculty of Science, University of Alexandria, Alexandria, Egypt
Get access Rights & Permissions [Opens in a new window]

Extract

In a previous paper (3) one of us reported an expansion for the exponential integral

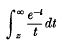
in terms of Bessel functions. In this note, we shall obtain the more general formula

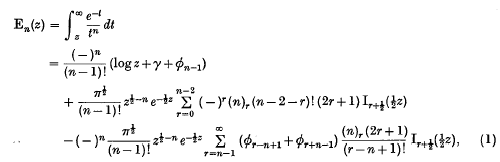
where n is any positive integer, γ is Euler's constant and

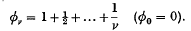
It reduces to that in (3) when n = 1.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 59 , Issue 4 , October 1963 , pp. 735 - 737
Copyright
Copyright © Cambridge Philosophical Society 1963

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bailey, W. N.Generalized hypergeometric series (Cambridge, 1935).Google Scholar
(2)Meligy, A. S.Quart. J. Math. Oxford Ser. (2), 10 (1959), 202.CrossRefGoogle Scholar
(3)Meligy, A. S.Proc. Cambridge Philos. Soc. 56 (1960), 233.CrossRefGoogle Scholar
(4)Slater, L. J.Confluent hypergeometric functions (Cambridge, 1960).Google Scholar
(5)Whittaker, E. T. and Watson, G. N.Modern analysis, 4th ed. (Cambridge, 1927).Google Scholar