On the dimension of the non-Cohen–Macaulay locus of local rings admitting dualizing complexes
Published online by Cambridge University Press: 24 October 2008
Extract
In this paper we mainly consider local rings admitting dualizing complexes. It is well-known that if a Noetherian local ring A admits a dualizing complex, then the non-Cohen–Macaulay (abbreviated CM) locus of A is closed in the Zariski topology (cf. [8, 10]). If the dimension of this locus is zero and A is equidimensional, i.e. the punctured spectrum of A is locally CM and dim(A/P) = dim (A) for all minimal prime ideals P ∈ Ass (A), then A is a generalized CM ring and its structure is well-understood (see [2, 12]). For instance, one of the characterizations of generalized CM rings is the conditions that for any parameter ideal q contained in a large power of the maximal ideal m of A, the difference between length and multiplicity
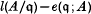
is independent of the choice of q. However, if the dimension of the non-CM locus is larger than zero, little is known about how this dimension is related to the structure of the local ring A. The purpose of this paper is to show that if M is a finitely generated A-module, then there exist systems of parameters x = (x1, …, xd) (where d = dim M) such that the difference
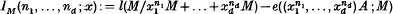
is a polynomial in n1, …, nd for all positive integers n1, …, nd and the degree of IM(n1, …, nd;x) is independent of the choice of x. We shall also give various characterizations of this degree by using the notion of reducing systems of parameters of Auslander and Buchsbaum[l]. In particular, if the module M is equidimensional we shall show that the degree of IM(n1, …, nd;x) is equal to the dimension of the non-CM locus of M.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 109 , Issue 3 , May 1991 , pp. 479 - 488
- Copyright
- Copyright © Cambridge Philosophical Society 1991
References
REFERENCES
- 17
- Cited by


