On the differentials in the Adams spectral sequence
Published online by Cambridge University Press: 24 October 2008
Extract
In this paper, we shall prove a result which identifies the differentials in the Adams spectral sequence (see (1,2)) with certain cohomology operations of higher kinds, in the sense of (4). This theorem will be stated precisely at the end of section 2, after a summary of the necessary information about the Adams spectral sequence and higher-order cohomology operations; the proof will follow in section 3. Finally, in section 4, we shall consider, by way of example, the Adams spectral sequence for the stable homotopy groups of spheres: we show how our theorem gives a proof of Liulevicius's result that 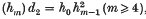 , where the elements hn (n ≥ 0) are base elements of
, where the elements hn (n ≥ 0) are base elements of
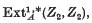
corresponding to the elements Sq2n in A, the mod 2 Steenrod algebra.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 60 , Issue 3 , July 1964 , pp. 409 - 420
- Copyright
- Copyright © Cambridge Philosophical Society 1964
References
REFERENCES
- 5
- Cited by


