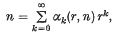Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Topping, D. M.
Cater, S.
Koh, Kwangil
Koh, Kwangil
Tikoo, Mohan Lal
Trollope, J. R.
BreMiller, R. S.
Sloyer, C. W.
Brillhart, John
Sanyal, Arun
von Randow, Rabe
Gilmer, R. W.
Levin, M. D.
Berberian, S. K.
Utz, W. R.
and
McCarthy, P. J.
1967.
Mathematical Notes.
The American Mathematical Monthly,
Vol. 74,
Issue. 6,
p.
680.
Stolarsky, Kenneth B.
1977.
Power and Exponential Sums of Digital Sums Related to Binomial Coefficient Parity.
SIAM Journal on Applied Mathematics,
Vol. 32,
Issue. 4,
p.
717.
Stolarsky, Kenneth B.
1978.
The binary digits of a power.
Proceedings of the American Mathematical Society,
Vol. 71,
Issue. 1,
p.
1.
Foster, D. M. E.
1987.
Estimates for a remainder term associated with the sum of digits function.
Glasgow Mathematical Journal,
Vol. 29,
Issue. 1,
p.
109.
Foster, D. M. E.
1991.
A lower bound for a remainder term associated with the sum of digits function.
Proceedings of the Edinburgh Mathematical Society,
Vol. 34,
Issue. 1,
p.
121.
Sándor, J.
and
Crstici, B.
2004.
Handbook of Number Theory II.
p.
329.
Chen, Louis H. Y.
Hwang, Hsien-Kuei
and
Zacharovas, Vytas
2014.
Distribution of the sum-of-digits function of random integers: A survey.
Probability Surveys,
Vol. 11,
Issue. none,
Lagarias, Jeffrey C
and
Mehta, Harsh
2016.
Products of binomial coefficients and unreduced Farey fractions.
International Journal of Number Theory,
Vol. 12,
Issue. 01,
p.
57.
Du, Lara
and
Lagarias, Jeffrey C.
2022.
Partial factorizations of products of binomial coefficients.
International Journal of Number Theory,
Vol. 18,
Issue. 03,
p.
691.