Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Verblunsky, S.
1930.
Note on the sum of an oscillating series, II.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 26,
Issue. 4,
p.
484.
Prasad, B. N.
1933.
On the summability (c, 1) of the conjugate series of aFourier series.
Annali di Matematica Pura ed Applicata,
Vol. 11,
Issue. 1,
p.
207.
Gergen, J. J.
and
Littauer, S. B.
1935.
Continuity and summability for double Fourier series.
Transactions of the American Mathematical Society,
Vol. 38,
Issue. 3,
p.
401.
Rogosinski, Werner
1936.
Abschnittsverhalten bei trigonometrischen und insbesondere Fourierschen Reihen.
Mathematische Zeitschrift,
Vol. 41,
Issue. 1,
p.
75.
Bosanquet, L. S.
1936.
Some arithmetic means connected with Fourier series.
Transactions of the American Mathematical Society,
Vol. 39,
Issue. 2,
p.
189.
Bosanquet, L. S.
and
Hyslop, J. M.
1937.
On the absolute summability of the Allied series of a fourier series.
Mathematische Zeitschrift,
Vol. 42,
Issue. 1,
p.
489.
Bhatnagar, P. L.
1938.
On the summability of the conjugate series of fourier series.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 7,
Issue. 2,
p.
85.
Bhatnagar, S. P.
1941.
On the Fourier coefficients of a discontinuous function.
Proceedings of the Edinburgh Mathematical Society,
Vol. 6,
Issue. 4,
p.
231.
Sekharan, K. Chandra
1943.
Bessel summation of series.
Proceedings of the Indian Academy of Sciences - Section A,
Vol. 17,
Issue. 6,
p.
219.
Sunouchi, Genichirô
1950.
Notes on Fourier analysis (XXV): Quasi-Tauberian theorem.
Tohoku Mathematical Journal,
Vol. 1,
Issue. 2,
Izumi, S.
Matsuyama, N.
and
Tsuchikura, T.
1953.
Notes on Fourier analysis (XLIX): Some negative examples.
Tohoku Mathematical Journal,
Vol. 5,
Issue. 1,
Agnew, Ralph Palmer
1959.
Riemann methods for evaluation of series.
Tohoku Mathematical Journal,
Vol. 11,
Issue. 3,
White, A. J.
1961.
On the restricted Cesàro summability of double Fourier series.
Transactions of the American Mathematical Society,
Vol. 99,
Issue. 2,
p.
308.
Yabuta, Kôzô
1970.
Some remarks on Wiener's quasi-tauberian theorems and the summability of Fourier series.
Tohoku Mathematical Journal,
Vol. 22,
Issue. 1,
Yabuta, Kôzô
1970.
Quasi-Tauberian theorems, applied to the summability of Fourier series by Riesz's logarithmic means.
Tohoku Mathematical Journal,
Vol. 22,
Issue. 1,
Rhoades, B. E.
1986.
Matrix summability of Fourier series based on inclusion theorems.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 100,
Issue. 3,
p.
545.
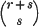 denote
denote