Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T02:46:15.044Z Has data issue: false hasContentIssue false
  • English
  • Français

On the asymptotic behaviour of sample spacings

Published online by Cambridge University Press:  24 October 2008

John Hawkes
John Hawkes
Affiliation:
University College of Swansea
Get access Rights & Permissions [Opens in a new window]

Summary

Suppose that we are given a random sample of size n chosen according to the uniform distribution on the unit interval. Let Zn(x) = Zn(x, ω) be the length of the unique left-closed and right-open sample spacing that contains x. The purpose of this paper is to examine the almost sure, and exceptional, growth rates of the process {Zn}. The typical maximum growth rate and the growth rate of the maximum can be of quite different orders of magnitude as is shown by the following two results.

Theorem 2. With probability one we have

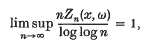
for almost all x.

Theorem 3. With probability one we have

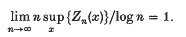
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 90 , Issue 2 , September 1981 , pp. 293 - 303
Copyright
Copyright © Cambridge Philosophical Society 1981

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Darling, D. A.On a class of problems related to the random division of an interval. Ann. Math. Statist. 24 (1953), 239–253.CrossRefGoogle Scholar
(2)Eggleston, H. G.Sets of fractional dimensions which occur in some problems in number theory. Proc. London Math. Soc. (2) 54 (1952), 42–93.CrossRefGoogle Scholar
(3)Feller, W.An introduction to probability theory and its applications, vol. 2, 2nd ed. (Wiley, New York, 1971).Google Scholar
(4)Flatto, L.A limit theorem for random coverings of a circle. Israel J. Math. 15 (1973), 167–184.CrossRefGoogle Scholar
(5)Kochen, S. and Stone, C.A note on the Borel-Cantelli lemma. Illinois J. Math. 8 (1964), 248–251.CrossRefGoogle Scholar
(6)Kôno, N.The Exact Hausdorff Measure of Irregularity Points for a Brownian Path. Z. Wahrsch. Verw. Gebiete. 40 (1977), 257–282.CrossRefGoogle Scholar
(7)Orey, S. and Tavlor, S. J.How often on a Brownian path does the law of the iterated logarithm fail? Proc. London Math. Soc. 28 (1974), 174–192.CrossRefGoogle Scholar
(8)Slud, E.Entropy and maximal spacings for random partitions. Z. Wahrsch. Verw. Gebiete. 41 (1978), 341–352.CrossRefGoogle Scholar
(9)Solomon, H.Geometric probability (SIAM, Philadelphia, 1978).CrossRefGoogle Scholar
(10)Steutel, F. W.Random division of an interval. Statistica Neerlandica 21 (1967), 231–244.CrossRefGoogle Scholar
(11)Stevens, W. L.Solution to a geometrical problem in probability. Ann. Eugenics 9 (1939), 315–320.CrossRefGoogle Scholar
(12)Whitworth, W. A.Choice and chance (Cambridge, 1897).Google Scholar