Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hall, R. R.
Huxley, M. N.
and
Wilson, J. C.
1995.
A three variable identity connected with Dedekind sums.
Periodica Mathematica Hungarica,
Vol. 30,
Issue. 3,
p.
189.
Lu, Hongwen
Jiao, Rongzheng
and
Ji, Chungang
2002.
Dedekind zeta-functions and Dedekind sums.
Science in China Series A: Mathematics,
Vol. 45,
Issue. 8,
p.
1059.
Borda, Bence
2017.
On the theorem of Davenport and generalized Dedekind sums.
Journal of Number Theory,
Vol. 172,
Issue. ,
p.
1.
Can, M.
2021.
Reciprocity formulas for Hall–Wilson–Zagier type Hardy–Berndt sums.
Acta Mathematica Hungarica,
Vol. 163,
Issue. 1,
p.
118.



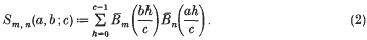
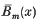 denotes the periodic extension into ℝ of the Bernoulli polynomial
denotes the periodic extension into ℝ of the Bernoulli polynomial