Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-24T16:47:43.634Z Has data issue: false hasContentIssue false
  • English
  • Français

On quadrature formulae

Published online by Cambridge University Press:  24 October 2008

Anders Reiz
Anders Reiz
Affiliation:
The Observatory, Lund, Sweden
Get access Rights & Permissions [Opens in a new window]

Extract

1. It is frequently required to find the numerical value of the definite integral 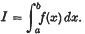It is, however, often found that even if the analytical expression of f(x) is given, it cannot be integrated in terms of known elementary functions. The elliptic integrals are perhaps the best known examples of functions of this type; and more common are cases where f(x) is not even defined by an analytical expression but merely specified by a table of numerical values. In the two cases mentioned one has to resort to a numerical integration procedure in which the integral is evaluated in terms of the values of f(x) at a finite number of the arguments x1, x2, …, xn. There are essentially two different types of quadrature formulae available, those which depend on the use of finite differences and the tabulation of f(x) at equidistant points, and those which depend on the values of f(x) at suitably selected points xi. These latter, so called mean-value methods, will be discussed in the present paper. For a recent treatment of such methods see, for example, Beard (5).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 46 , Issue 1 , January 1950 , pp. 119 - 126
Copyright
Copyright © Cambridge Philosophical Society 1950

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Moors, B. P.Verh. K. Akad. Wet. Amsterdam, I Sectie, Del. 11 (1913).Google Scholar
(2)Steffensen, J. F.Skand. Aktuar Tidskr. 28 (1945), 1.Google Scholar
(3)Radau, R.J. Math. 6 (1880).Google Scholar
(4)Irwin, J. O.Quadrature and cubature formulae. Tracts for Computers, x (1923), 10.Google Scholar
Whittaker, E. T. and Robinson, G.The calculus of observations (1st ed., Glasgow, 1924), 161.Google Scholar
(5)Beard, R. E.J. Inst. Actu. 73 (1948), 356.CrossRefGoogle Scholar