Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-24T16:58:08.951Z Has data issue: false hasContentIssue false
  • English
  • Français

On positive harmonic functions

Published online by Cambridge University Press:  24 October 2008

A. C. Allen
A. C. Allen
Affiliation:
PeterHouseCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Any harmonic function which is defined and positive in the half-plane η > 0 may be expressed by

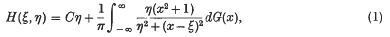
where C is a non-negative number, and G(x) is a bounded non-decreasing function. For a simple proof see Loomis and Widder (2). Let us write

where w(z) is a regular function of z in η > 0, and satisfies the following conditions: (i) w(z) is real and continuous at all points of the open interval (a, b) of the real axis [the interval may be unbounded]; (ii) there exists a simply connected domain Δ, lying in the half-plane η > 0, whose frontier contains the interval (a, b) of the real axis and which is mapped ‘simply’ on the half-plane υ > 0 by the conformal transformation w = w(z).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 48 , Issue 4 , October 1952 , pp. 571 - 577
Copyright
Copyright © Cambridge Philosophical Society 1952

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Loomis, L. H.Trans. Amer. math. Soc. 53 (1943), 239–50.Google Scholar
(2)Loomis, L. H. and Widder, D. V.Duke math. J. 9 (1942), 643–5.Google Scholar
(3)Verblunsky, S.Proc. Camb. phil. Soc. 44 (1948), 289–91.CrossRefGoogle Scholar