Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Brown, Gavin
and
Moran, William
1975.
Coin tossing and powers of singular measures.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 77,
Issue. 2,
p.
349.
Brown, Gavin
and
Hewitt, Edwin
1976.
Continuous singular measures equivalent to their convolution squares.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 80,
Issue. 2,
p.
249.
Graham, Colin C.
1977.
Functional calculus and positive-definite functions.
Transactions of the American Mathematical Society,
Vol. 231,
Issue. 1,
p.
215.
Maclean, Alan
1978.
Products of singular continuous measures.
Proceedings of the American Mathematical Society,
Vol. 68,
Issue. 1,
p.
85.
Ritter, G.
1979.
On Kakutani's dichotomy theorem for infinite products of not necessarily independent functions.
Mathematische Annalen,
Vol. 239,
Issue. 1,
p.
35.
Ritter, G.
1979.
On dichotomy of Riesz products.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 85,
Issue. 1,
p.
79.
MacLean, Alan
1980.
Modifications of Fourier transforms and singular continuous measures.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 87,
Issue. 3,
p.
383.
Brown, Gavin
and
Moran, William
1980.
Maximal elements in the maximal ideal space of a measure algebra.
Mathematische Annalen,
Vol. 246,
Issue. 2,
p.
131.
Brown, Gavin
and
Mohan, William
1982.
Probability measures with trivial Stam groups.
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 91,
Issue. 3,
p.
477.
Freedman, David
and
Pitman, Jim
1990.
A measure which is singular and uniformly locally uniform.
Proceedings of the American Mathematical Society,
Vol. 108,
Issue. 2,
p.
371.
Koumandos, Stamatis
1992.
Probabilistic and Stochastic Methods in Analysis, with Applications.
p.
605.
Koumandos, Stamatis
1994.
Lp-convergence of a certain class of product martingales.
Proceedings of the Edinburgh Mathematical Society,
Vol. 37,
Issue. 2,
p.
243.
Dooley, A. H.
and
Eigen, S. J.
1996.
A Family of Generalized Riesz Products.
Canadian Journal of Mathematics,
Vol. 48,
Issue. 2,
p.
302.
Houcein, El
and
Abdalaoui, El
1999.
La singularité mutuelle presque sûre du spectre des transformations d’Ornstein.
Israel Journal of Mathematics,
Vol. 112,
Issue. 1,
p.
135.
Fan, Aihua
and
Zhang, Xiongying
2009.
Some Properties of Riesz Products on the Ring of p-Adic Integers.
Journal of Fourier Analysis and Applications,
Vol. 15,
Issue. 4,
p.
521.
Zhang, Xiong-Ying
2009.
Riesz products on the ring of dyadic integers.
Journal of Mathematical Analysis and Applications,
Vol. 357,
Issue. 1,
p.
103.
Wu, Huai-Bing
and
Zhang, Xiong-Ying
2013.
Some remarks onp-adic Riesz products.
Journal of Mathematical Analysis and Applications,
Vol. 403,
Issue. 1,
p.
5.
PARREAU, FRANÇOIS
and
ROY, EMMANUEL
2015.
Prime Poisson suspensions.
Ergodic Theory and Dynamical Systems,
Vol. 35,
Issue. 7,
p.
2216.
Ohrysko, Przemysław
Wojciechowski, Michał
and
Graham, Colin C.
2016.
Non-separability of the Gelfand space of measure algebras.
Arkiv för Matematik,
Vol. 54,
Issue. 2,
p.
525.
Boshernitzan, Michael
Frantzikinakis, Nikos
and
Wierdl, Máté
2017.
Under-recurrence in the Khintchine recurrence theorem.
Israel Journal of Mathematics,
Vol. 222,
Issue. 2,
p.
815.


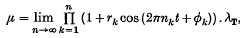
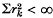 ) or µ is purely singular (when
) or µ is purely singular (when 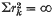 ).
).