Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T15:34:53.133Z Has data issue: false hasContentIssue false
  • English
  • Français

On functionally constant invariants of the Riemann tensor

Published online by Cambridge University Press:  24 October 2008

H. A. Buchdahl
H. A. Buchdahl
Affiliation:
Department of Applied Mathematics and Theoretical PhysicsUniversity of Cambridge
Get access Rights & Permissions [Opens in a new window]

Abstract

In any V4 two quadratic invariants of the Riemann tensor, J4 and K4, say, are known which are functionally constant, i.e. the Hamiltonian derivatives of which vanish identically. Certain natural generalizations, J2n and K2n, of degree n of these are considered, J2n being defined in any Vm but K2n only in a V2n. It is shown by methods having purely local character that J2n is functionally constant in any V2n, and that K2n vanishes identically when n is odd or when n is even and the V2n is either conformally flat or admits a hypersurface-orthogonal Killing vector; whilst in a V4n it is functionally constant. These results follow upon a prior spinorial treatment of the special case n = 3 which leads to an explicit expression for a pseudo-vector density of which the scalar density 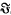6 is the divergence. Finally, it is shown that for appropriate values of n there exist functionally constant invariants other than J2n and K2n

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 68 , Issue 1 , July 1970 , pp. 179 - 185
Copyright
Copyright © Cambridge Philosophical Society 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1) Bach, R.Math. Z. 9 (1921), 100.CrossRefGoogle Scholar
(2) Lanczos, C.Ann. of Math. 39 (1938), 842.CrossRefGoogle Scholar
(3) Buchdahl, H. A.J. Mathematical Phys. 1 (1960), 537.CrossRefGoogle Scholar
(4) Buchdahl, H. A.J. Austral. Math. Soc. 6 (1966), 424.CrossRefGoogle Scholar
(5) Chern, S.-S.J. Soc. Indust. Appl. Math. 10 (1962), 751.CrossRefGoogle Scholar
(6) Buchdahl, H. A.Proc. Roy. Soc. Ser A 303 (1968), 355.Google Scholar