On fourfolds with canonical curve sections
Published online by Cambridge University Press: 24 October 2008
Extract
In a recent note the writer has examined the varieties 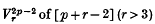 whose generic curve sections are canonical curves of genus p, of general character, and whose surface sections contain only complete intersections with primals; following Fano's classification, we call these varieties of the first species. Such varieties are all rational provided that r > 3 and p > 6. In the present paper we consider their representations on linear spaces for the case r = 4, from which, in conjunction with the previous results, we conclude that fourfolds of the first species exist if, and only if, p ≤ 10; this agrees with the conjecture made by Fano in the case r = 3. It will be seen that the representation of these varieties on [4] provides interesting illustrations of Semple's formulae for composite surfaces in higher space.
whose generic curve sections are canonical curves of genus p, of general character, and whose surface sections contain only complete intersections with primals; following Fano's classification, we call these varieties of the first species. Such varieties are all rational provided that r > 3 and p > 6. In the present paper we consider their representations on linear spaces for the case r = 4, from which, in conjunction with the previous results, we conclude that fourfolds of the first species exist if, and only if, p ≤ 10; this agrees with the conjecture made by Fano in the case r = 3. It will be seen that the representation of these varieties on [4] provides interesting illustrations of Semple's formulae for composite surfaces in higher space.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 46 , Issue 3 , July 1950 , pp. 419 - 428
- Copyright
- Copyright © Cambridge Philosophical Society 1950
References
* Roth, , Ann. Mat. (4), 28 (1949), 91.CrossRefGoogle Scholar
† Fano, , Comm. Math. Helvetici, 14 (1941), 203.Google Scholar
‡ Semple, , Proc. Roy. Irish Acad. A, 41 (1933), 70.Google Scholar
* Actually we require not the characters of the curve but those of the scroll generated by the lines.
† See the works already quoted.
‡ See Segre, , Encyk. Math. Wiss. iii C 7, 954.Google Scholar
§ Cf. Semple, and Roth, , Algebraic Geometry (Oxford, 1949), p. 20.Google Scholar
* Scritti offerti a L. Berzolari (Pavia, 1936), p. 329.Google Scholar
† Seven, , Mem. Accad. Torino (2), 52 (1903), 61.Google Scholar
‡ In the usual notation, a primal of order l in [4] has δ nodes at simple points of a generic surface F, where
§ In the first of his works quoted.
* Cf. Semple and Roth, op. cit. p. 120.
† Roth, , Proc. Cambridge Phil. Soc. 25 (1929), 390.CrossRefGoogle Scholar
‡ See Semple and Roth, op. cit. p. 280.
§ Fano, , R.C. Accad. Lincei (6), 11 (1930), 329.Google Scholar
* Roth, , Proc. Cambridge Phil. Soc. 29 (1933), 184.CrossRefGoogle Scholar
* Semple and Roth, op. cit. p. 155.
† For an account of adjoint threefolds in relation to the base elements of a system, see Fano, , Comm. Pont. Acad. Scient. 11 (1947), 635.Google Scholar The theory for fourfolds is analogous to this.
* Fano, , Comm. Math. Helvetici, 14 (1941), 203.Google Scholar
* Fano, , R.C. Accad. Lincei (8), 6 (1949), 151.Google Scholar
- 2
- Cited by


