Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T03:14:34.312Z Has data issue: false hasContentIssue false
  • English
  • Français

On epimorphisms of non-commutative rings

Published online by Cambridge University Press:  24 October 2008

J. T. Knight
J. T. Knight
Affiliation:
Churchill College, Cambridge
Get access Rights & Permissions [Opens in a new window]

Extract

From a commutative ring A, Lazard(8) has made a flat injective epimorphism: A → B of commutative rings, such that if A → C is another flat injective epimorphism of commutative rings, then there is one and only one ring morphism: B → C such that the diagram

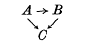
commutes; and he shows too that B → C is a flat injective epimorphism. The main aim of the present paper is to make a similar object for not necessarily commutative rings: this is achieved thanks to the notion of an A-prering, intermediate between that of an A-bimodule and that of an A-ring. In passing, prerings are also used to construct a kind of non-commutative ring of fractions.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 68 , Issue 3 , November 1970 , pp. 589 - 600
Copyright
Copyright © Cambridge Philosophical Society 1970

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bergman, G. Notes on epimorphisms of rings; unpublished.Google Scholar
(2)Bergman, G. Modules over free products of rings; unpublished.Google Scholar
(3)Bergman, G. Commuting elements in free algebras and related topics in ring theory; thesis, Harvard, 1967.Google Scholar
(4)Bourbaki, N.Elements de mathérnatique, Paris, at various times.Google Scholar
(5)Cohn, P. M.On the free product of associative rings. Math. Z. 71 (1959), 380–398.Google Scholar
(6)Cohn, P. M.Free associative algebras. Bull. London Math. Soc. 1 (1969), 1–39.Google Scholar
(7)Freyd, P.Abelian categories (New York, 1964).Google Scholar
(8)Lazard, D. Exposé 4 of Les épimorphismes d'anneaux, Séminaire Samuel (Paris, 1968).Google Scholar
(9)Mazet, P. Exposé 2. Les épimorphismes d'anneaux, Séminaire Samuel (Paris, 1968).Google Scholar
(10)Roby, N. Exposé 3. Les épimorphismes d'anneaux, Séminaire Samuel (Paris, 1968).Google Scholar
(11)Silver, L.Noncommutative localizations and applications. J. Algebra 7 (1967), 44–76; section 1.Google Scholar