No CrossRef data available.
On convex sets and measures
Published online by Cambridge University Press: 24 October 2008
Extract
If α is a positive real number then, for each set E in R3, we define
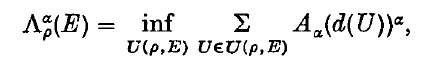
where U(ρ, E) is any countable collection of convex sets, each of diameter at most ρ, whose union covers E, and Aα is a positive real number. Then the convex α-dimensional measure Λα(E), of E, is 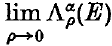 . In this paper we shall only be considering the cases α = 1,2 where, as is usual, we take A1 = 1 and A2 = ¼π. The symbols
. In this paper we shall only be considering the cases α = 1,2 where, as is usual, we take A1 = 1 and A2 = ¼π. The symbols 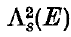 ,Λs(E) will denote the spherical (circular) measure of E, i.e. when the coverings are restricted to being collections of spheres (circles), and E(z) is the intersection of a set E (in R3) with the plane (x, y) at z.
,Λs(E) will denote the spherical (circular) measure of E, i.e. when the coverings are restricted to being collections of spheres (circles), and E(z) is the intersection of a set E (in R3) with the plane (x, y) at z.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 62 , Issue 1 , January 1966 , pp. 33 - 42
- Copyright
- Copyright © Cambridge Philosophical Society 1966


